BioFVM warmup: 2D continuum simulation of tumor growth
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM. See also the guides to setting up a C++ compiler in Windows or OSX.
What you’ll need
- A working C++ development environment with support for OpenMP. See these prior tutorials if you need help.
- A download of BioFVM, available at http://BioFVM.MathCancer.org and http://BioFVM.sf.net. Use Version 1.0.3 or later.
- Matlab or Octave for visualization. Matlab might be available for free at your university. Octave is open source and available from a variety of sources.
Our modeling task
We will implement a basic 2-D model of tumor growth in a heterogeneous microenvironment, with inspiration by glioblastoma models by Kristin Swanson, Russell Rockne and others (e.g., this work), and continuum tumor growth models by Hermann Frieboes, John Lowengrub, and our own lab (e.g., this paper and this paper).
We will model tumor growth driven by a growth substrate, where cells die when the growth substrate is insufficient. The tumor cells will have motility. A continuum blood vasculature will supply the growth substrate, but tumor cells can degrade this existing vasculature. We will revisit and extend this model from time to time in future tutorials.
Mathematical model
Taking inspiration from the groups mentioned above, we’ll model a live cell density ρ of a relatively low-adhesion tumor cell species (e.g., glioblastoma multiforme). We’ll assume that tumor cells move randomly towards regions of low cell density (modeled as diffusion with motility μ). We’ll assume that that the net birth rate rB is proportional to the concentration of growth substrate σ, which is released by blood vasculature with density b. Tumor cells can degrade the tissue and hence this existing vasculature. Tumor cells die at rate rD when the growth substrate level is too low. We assume that the tumor cell density cannot exceed a max level ρmax. A model that includes these effects is:
\[ \frac{ \partial \rho}{\partial t} = \mu \nabla^2 \rho + r_B(\sigma)\rho \left( 1 – \frac{ \rho}{\rho_\textrm{max}} \right) – r_D(\sigma) \rho \]
\[ \frac{ \partial b}{\partial t} = – r_\textrm{degrade} \rho b \]
\[ \frac{\partial \sigma}{ \partial t} = D\nabla^2 \sigma – \lambda_a \sigma – \lambda_2 \rho \sigma + r_\textrm{deliv}b \left( \sigma_\textrm{max} – \sigma \right) \]
where for the birth and death rates, we’ll use the constitutive relations:
\[ r_B(\sigma) = r_B \textrm{ max} \left( \frac{\sigma – \sigma_\textrm{min}}{ \sigma_\textrm{ max} – \sigma_\textrm{min} } , 0 \right)\]
\[r_D(\sigma) = r_D \textrm{ max} \left( \frac{ \sigma_\textrm{min} – \sigma}{\sigma_\textrm{min}} , 0 \right) \]
Mapping the model onto BioFVM
BioFVM solves on a vector u of substrates. We’ll set u = [ρ , b, σ ]. The code expects PDEs of the general form:
\[ \frac{\partial q}{\partial t} = D\nabla^2 q – \lambda q + S\left( q^* – q \right) – Uq\]
So, we determine the decay rate (λ), source function (S), and uptake function (U) for the cell density ρ and the growth substrate σ.
Cell density
We first slightly rewrite the PDE:
\[ \frac{ \partial \rho}{\partial t} = \mu \nabla^2 \rho + r_B(\sigma) \frac{ \rho}{\rho_\textrm{max}} \left( \rho_\textrm{max} – \rho \right) – r_D(\sigma)\rho \]
and then try to match to the general form term-by-term. While BioFVM wasn’t intended for solving nonlinear PDEs of this form, we can make it work by quasi-linearizing, with the following functions:
\[ S = r_B(\sigma) \frac{ \rho }{\rho_\textrm{max}} \hspace{1in} U = r_D(\sigma). \]
When implementing this, we’ll evaluate σ and ρ at the previous time step. The diffusion coefficient is μ, and the decay rate is zero. The target or saturation density is ρmax.
Growth substrate
Similarly, by matching the PDE for σ term-by-term with the general form, we use:
\[ S = r_\textrm{deliv}b, \hspace{1in} U = \lambda_2 \rho. \]
The diffusion coefficient is D, the decay rate is λ1, and the saturation density is σmax.
Blood vessels
Lastly, a term-by-term matching of the blood vessel equation gives the following functions:
\[ S=0 \hspace{1in} U = r_\textrm{degrade}\rho. \]
The diffusion coefficient, decay rate, and saturation density are all zero.
Implementation in BioFVM
- Start a project: Create a new directory for your project (I’d recommend “BioFVM_2D_tumor”), and enter the directory. Place a copy of BioFVM (the zip file) into your directory. Unzip BioFVM, and copy BioFVM*.h, BioFVM*.cpp, and pugixml* files into that directory.
- Copy the matlab visualization files: To help read and plot BioFVM data, we have provided matlab files. Copy all the *.m files from the matlab subdirectory to your project.
- Copy the empty project: BioFVM Version 1.0.3 or later includes a template project and Makefile to make it easier to get started. Copy the Makefile and template_project.cpp file to your project. Rename template_project.cpp to something useful, like 2D_tumor_example.cpp.
- Edit the makefile: Open a terminal window and browse to your project. Tailor the makefile to your new project:
notepad++ Makefile
Change the PROGRAM_NAME to 2Dtumor.
Also, rename main to 2D_tumor_example throughout the Makefile.
Lastly, note that if you are using OSX, you’ll probably need to change from “g++” to your installed compiler. See these tutorials.
- Start adapting 2D_tumor_example.cpp: First, open 2D_tumor_example.cpp:
notepad++ 2D_tumor_example.cpp
Just after the “using namespace BioFVM” section of the code, define useful globals. Here and throughout, new and/or modified code is in blue:
using namespace BioFVM: // helpful -- have indices for each "species" int live_cells = 0; int blood_vessels = 1; int oxygen = 2; // some globals double prolif_rate = 1.0 /24.0; double death_rate = 1.0 / 6; // double cell_motility = 50.0 / 365.25 / 24.0 ; // 50 mm^2 / year --> mm^2 / hour double o2_uptake_rate = 3.673 * 60.0; // 165 micron length scale double vessel_degradation_rate = 1.0 / 2.0 / 24.0 ; // 2 days to disrupt tissue double max_cell_density = 1.0; double o2_supply_rate = 10.0; double o2_normoxic = 1.0; double o2_hypoxic = 0.2;
- Set up the microenvironment: Within main(), make sure we have the right number of substrates, and set them up:
// create a microenvironment, and set units Microenvironment M; M.name = "Tumor microenvironment"; M.time_units = "hr"; M.spatial_units = "mm"; M.mesh.units = M.spatial_units; // set up and add all the densities you plan M.set_density( 0 , "live cells" , "cells" ); M.add_density( "blood vessels" , "vessels/mm^2" ); M.add_density( "oxygen" , "cells" ); // set the properties of the diffusing substrates M.diffusion_coefficients[live_cells] = cell_motility; M.diffusion_coefficients[blood_vessels] = 0; M.diffusion_coefficients[oxygen] = 6.0; // 1e5 microns^2/min in units mm^2 / hr M.decay_rates[live_cells] = 0; M.decay_rates[blood_vessels] = 0; M.decay_rates[oxygen] = 0.01 * o2_uptake_rate; // 1650 micron length scale
Notice how our earlier global definitions of “live_cells”, “blood_vessels”, and “oxygen” makes it easier to make sure we’re referencing the correct substrates in lines like these.
- Resize the domain and test: For this example (and so the code runs very quickly), we’ll work in 2D in a 2 cm × 2 cm domain:
// set the mesh size double dx = 0.05; // 50 microns M.resize_space( 0.0 , 20.0 , 0, 20.0 , -dx/2.0, dx/2.0 , dx, dx, dx );
Notice that we use a tissue thickness of dx/2 to use the 3D code for a 2D simulation. Now, let’s test:
make 2Dtumor
Go ahead and cancel the simulation [Control]+C after a few seconds. You should see something like this:
Starting program ... Microenvironment summary: Tumor microenvironment: Mesh information: type: uniform Cartesian Domain: [0,20] mm x [0,20] mm x [-0.025,0.025] mm resolution: dx = 0.05 mm voxels: 160000 voxel faces: 0 volume: 20 cubic mm Densities: (3 total) live cells: units: cells diffusion coefficient: 0.00570386 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 75523.9 mm blood vessels: units: vessels/mm^2 diffusion coefficient: 0 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 0 mm oxygen: units: cells diffusion coefficient: 6 mm^2 / hr decay rate: 2.2038 hr^-1 diffusion length scale: 1.65002 mm simulation time: 0 hr (100 hr max) Using method diffusion_decay_solver__constant_coefficients_LOD_3D (implicit 3-D LOD with Thomas Algorithm) ... simulation time: 10 hr (100 hr max) simulation time: 20 hr (100 hr max)
- Set up initial conditions: We’re going to make a small central focus of tumor cells, and a “bumpy” field of blood vessels.
// set initial conditions // use this syntax to create a zero vector of length 3 // std::vector<double> zero(3,0.0); std::vector<double> center(3); center[0] = M.mesh.x_coordinates[M.mesh.x_coordinates.size()-1] /2.0; center[1] = M.mesh.y_coordinates[M.mesh.y_coordinates.size()-1] /2.0; center[2] = 0; double radius = 1.0; std::vector<double> one( M.density_vector(0).size() , 1.0 ); double pi = 2.0 * asin( 1.0 ); // use this syntax for a parallelized loop over all the // voxels in your mesh: #pragma omp parallel for for( int i=0; i < M.number_of_voxels() ; i++ ) { std::vector<double> displacement = M.voxels(i).center – center; double distance = norm( displacement ); if( distance < radius ) { M.density_vector(i)[live_cells] = 0.1; } M.density_vector(i)[blood_vessels]= 0.5 + 0.5*cos(0.4* pi * M.voxels(i).center[0])*cos(0.3*pi *M.voxels(i).center[1]); M.density_vector(i)[oxygen] = o2_normoxic; } - Change to a 2D diffusion solver:
// set up the diffusion solver, sources and sinks M.diffusion_decay_solver = diffusion_decay_solver__constant_coefficients_LOD_2D;
- Set the simulation times: We’ll simulate 10 days, with output every 12 hours.
double t = 0.0; double t_max = 10.0 * 24.0; // 10 days double dt = 0.1; double output_interval = 12.0; // how often you save data double next_output_time = t; // next time you save data
- Set up the source function:
void supply_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] static double temp1 = prolif_rate / ( o2_normoxic – o2_hypoxic ); (*write_here)[live_cells] = microenvironment->density_vector(voxel_index)[oxygen]; (*write_here)[live_cells] -= o2_hypoxic; if( (*write_here)[live_cells] < 0.0 ) { (*write_here)[live_cells] = 0.0; } else { (*write_here)[live_cells] = temp1; (*write_here)[live_cells] *= microenvironment->density_vector(voxel_index)[live_cells]; } (*write_here)[blood_vessels] = 0.0; (*write_here)[oxygen] = o2_supply_rate; (*write_here)[oxygen] *= microenvironment->density_vector(voxel_index)[blood_vessels]; return; }Notice the use of the static internal variable temp1: the first time this function is called, it declares this helper variable (to save some multiplication operations down the road). The static variable is available to all subsequent calls of this function.
- Set up the target function (substrate saturation densities):
void supply_target_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] (*write_here)[live_cells] = max_cell_density; (*write_here)[blood_vessels] = 1.0; (*write_here)[oxygen] = o2_normoxic; return; } - Set up the uptake function:
void uptake_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] (*write_here)[live_cells] = o2_hypoxic; (*write_here)[live_cells] -= microenvironment->density_vector(voxel_index)[oxygen]; if( (*write_here)[live_cells] < 0.0 ) { (*write_here)[live_cells] = 0.0; } else { (*write_here)[live_cells] *= death_rate; } (*write_here)[oxygen] = o2_uptake_rate ; (*write_here)[oxygen] *= microenvironment->density_vector(voxel_index)[live_cells]; (*write_here)[blood_vessels] = vessel_degradation_rate ; (*write_here)[blood_vessels] *= microenvironment->density_vector(voxel_index)[live_cells]; return; }
And that’s it. The source should be ready to go!
Source files
You can download completed source for this example here:
Using the code
Running the code
First, compile and run the code:
make 2Dtumor
The output should look like this.
Starting program … Microenvironment summary: Tumor microenvironment: Mesh information: type: uniform Cartesian Domain: [0,20] mm x [0,20] mm x [-0.025,0.025] mm resolution: dx = 0.05 mm voxels: 160000 voxel faces: 0 volume: 20 cubic mm Densities: (3 total) live cells: units: cells diffusion coefficient: 0.00570386 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 75523.9 mm blood vessels: units: vessels/mm^2 diffusion coefficient: 0 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 0 mm oxygen: units: cells diffusion coefficient: 6 mm^2 / hr decay rate: 2.2038 hr^-1 diffusion length scale: 1.65002 mm simulation time: 0 hr (240 hr max) Using method diffusion_decay_solver__constant_coefficients_LOD_2D (2D LOD with Thomas Algorithm) … simulation time: 12 hr (240 hr max) simulation time: 24 hr (240 hr max) simulation time: 36 hr (240 hr max) simulation time: 48 hr (240 hr max) simulation time: 60 hr (240 hr max) simulation time: 72 hr (240 hr max) simulation time: 84 hr (240 hr max) simulation time: 96 hr (240 hr max) simulation time: 108 hr (240 hr max) simulation time: 120 hr (240 hr max) simulation time: 132 hr (240 hr max) simulation time: 144 hr (240 hr max) simulation time: 156 hr (240 hr max) simulation time: 168 hr (240 hr max) simulation time: 180 hr (240 hr max) simulation time: 192 hr (240 hr max) simulation time: 204 hr (240 hr max) simulation time: 216 hr (240 hr max) simulation time: 228 hr (240 hr max) simulation time: 240 hr (240 hr max) Done!
Looking at the data
Now, let’s pop it open in matlab (or octave):
matlab
To load and plot a single time (e.g., the last tim)
!ls *.mat M = read_microenvironment( 'output_240.000000.mat' ); plot_microenvironment( M );
To add some labels:
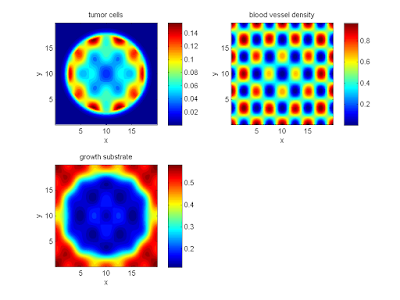
labels{1} = 'tumor cells';
labels{2} = 'blood vessel density';
labels{3} = 'growth substrate';
plot_microenvironment( M ,labels );
Your output should look a bit like this:
Lastly, you might want to script the code to create and save plots of all the times.
labels{1} = 'tumor cells';
labels{2} = 'blood vessel density';
labels{3} = 'growth substrate';
for i=0:20
t = i*12;
input_file = sprintf( 'output_%3.6f.mat', t );
output_file = sprintf( 'output_%3.6f.png', t );
M = read_microenvironment( input_file );
plot_microenvironment( M , labels );
print( gcf , '-dpng' , output_file );
end
What’s next
We’ll continue posting new tutorials on adapting BioFVM to existing and new simulators, as well as guides to new features as we roll them out.
Stay tuned and watch this blog!
2 thoughts on “BioFVM warmup: 2D continuum simulation of tumor growth”
Comments are closed.
For those who want to use Python to visualize results, the following script should help:
# plot_microenvironment.py – plot results from
# http://www.mathcancer.org/blog/biofvm-warmup-2d-continuum-simulation-of-tumor-growth/
# (Requires Python modules: scipy and matplotlib)
import sys
import os.path
import scipy.io
import matplotlib.pyplot as plt
“”” —- Sample use:
python plot_microenvironment.py “output_240.000000.mat” 4 “tumor cells”
python plot_microenvironment.py “output_240.000000.mat” 5 “blood vessel density”
python plot_microenvironment.py “output_240.000000.mat” 6 “growth substrate”
———-“””
print(“len(sys.argv) =”,len(sys.argv))
# 4=tumor cells field, 5=blood vessel density, 6=growth substrate
if (len(sys.argv) < 4):
print("Usage: %s
Uh, apparently there’s a limit to the length of a reply. Ah well, track me down & email me if you’re interested.