Category: diffusion
Setting up the PhysiCell microenvironment with XML

As of release 1.6.0, users can define all the chemical substrates in the microenvironment with an XML configuration file. (These are stored by default in ./config/. The default parameter file is ./config/PhysiCell_settings.xml.) This should make it much easier to set up the microenvironment (previously required a lot of manual C++), as well as make it easier to change parameters and initial conditions.
In release 1.7.0, users gained finer grained control on Dirichlet conditions: individual Dirichlet conditions can be enabled or disabled for each individual diffusing substrate on each individual boundary. See details below.
This tutorial will show you the key techniques to use these features. (See the User_Guide for full documentation.) First, let’s create a barebones 2D project by populating the 2D template project. In a terminal shell in your root PhysiCell directory, do this:
make template2D
We will use this 2D project template for the remainder of the tutorial. We assume you already have a working copy of PhysiCell installed, version 1.6.0 or later. (If not, visit the PhysiCell tutorials to find installation instructions for your operating system.) You will need version 1.7.0 or later to control Dirichlet conditions on individual boundaries.
You can download the latest version of PhysiCell at:
- GitHub: https://github.com/MathCancer/PhysiCell/releases
- SourceForge: https://sourceforge.net/projects/physicell/files/latest/download
Microenvironment setup in the XML configuration file
Next, let’s look at the parameter file. In your text editor of choice, open up ./config/PhysiCell_settings.xml, and browse down to <microenvironment_setup>:
<microenvironment_setup> <variable name="oxygen" units="mmHg" ID="0"> <physical_parameter_set> <diffusion_coefficient units="micron^2/min">100000.0</diffusion_coefficient> <decay_rate units="1/min">0.1</decay_rate> </physical_parameter_set> <initial_condition units="mmHg">38.0</initial_condition> <Dirichlet_boundary_condition units="mmHg" enabled="true">38.0</Dirichlet_boundary_condition> </variable> <options> <calculate_gradients>false</calculate_gradients> <track_internalized_substrates_in_each_agent>false</track_internalized_substrates_in_each_agent> <!-- not yet supported --> <initial_condition type="matlab" enabled="false"> <filename>./config/initial.mat</filename> </initial_condition> <!-- not yet supported --> <dirichlet_nodes type="matlab" enabled="false"> <filename>./config/dirichlet.mat</filename> </dirichlet_nodes> </options> </microenvironment_setup>
Notice a few trends:
- The <variable> XML element (tag) is used to define a chemical substrate in the microenvironment. The attributes say that it is named oxygen, and the units of measurement are mmHg. Notice also that the ID is 0: this unique integer identifier helps for finding and accessing the substrate within your PhysiCell project. Make sure your first substrate ID is 0, since C++ starts indexing at 0.
- Within the <variable> block, we set the properties of this substrate:
- <diffusion_coefficient> sets the (uniform) diffusion constant for the substrate.
- <decay_rate> is the substrate’s background decay rate.
- <initial_condition> is the value the substrate will be (uniformly) initialized to throughout the domain.
- <Dirichlet_boundary_condition> is the value the substrate will be set to along the outer computational boundary throughout the simulation, if you set enabled=true. If enabled=false, then PhysiCell (via BioFVM) will use Neumann (zero flux) conditions for that substrate.
- The <options> element helps configure other simulation behaviors:
- Use <calculate_gradients> to control whether PhysiCell computes all chemical gradients at each time step. Set this to true to enable accurate gradients (e.g., for chemotaxis).
- Use <track_internalized_substrates_in_each_agent> to enable or disable the PhysiCell feature of actively tracking the total amount of internalized substrates in each individual agent. Set this to true to enable the feature.
- <initial_condition> is reserved for a future release where we can specify non-uniform initial conditions as an external file (e.g., a CSV or Matlab file). This is not yet supported.
- <dirichlet_nodes> is reserved for a future release where we can specify Dirchlet nodes at any location in the simulation domain with an external file. This will be useful for irregular domains, but it is not yet implemented.
Note that PhysiCell does not convert units. The units attributes are helpful for clarity between users and developers, to ensure that you have worked in consistent length and time units. By default, PhysiCell uses minutes for all time units, and microns for all spatial units.
Changing an existing substrate
Let’s modify the oxygen variable to do the following:
- Change the diffusion coefficient to 120000 \(\mu\mathrm{m}^2 / \mathrm{min}\)
- Change the initial condition to 40 mmHg
- Change the oxygen Dirichlet boundary condition to 42.7 mmHg
- Enable gradient calculations
If you modify the appropriate fields in the <microenvironment_setup> block, it should look like this:
<microenvironment_setup> <variable name="oxygen" units="mmHg" ID="0"> <physical_parameter_set> <diffusion_coefficient units="micron^2/min">120000.0</diffusion_coefficient> <decay_rate units="1/min">0.1</decay_rate> </physical_parameter_set> <initial_condition units="mmHg">40.0</initial_condition> <Dirichlet_boundary_condition units="mmHg" enabled="true">42.7</Dirichlet_boundary_condition> </variable> <options> <calculate_gradients>true</calculate_gradients> <track_internalized_substrates_in_each_agent>false</track_internalized_substrates_in_each_agent> <!-- not yet supported --> <initial_condition type="matlab" enabled="false"> <filename>./config/initial.mat</filename> </initial_condition> <!-- not yet supported --> <dirichlet_nodes type="matlab" enabled="false"> <filename>./config/dirichlet.mat</filename> </dirichlet_nodes> </options> </microenvironment_setup>
Adding a new diffusing substrate
Let’s add a new dimensionless substrate glucose with the following:
- Diffusion coefficient is 18000 \(\mu\mathrm{m}^2 / \mathrm{min}\)
- No decay rate
- The initial condition is 1 (dimensionless)
- Neumann (no flux) boundary conditions
To add the new variable, I suggest copying an existing variable (in this case, oxygen) and modifying to:
- change the name and units throughout
- increase the ID by one
- write in the appropriate initial and boundary conditions
If you modify the appropriate fields in the <microenvironment_setup> block, it should look like this:
<microenvironment_setup> <variable name="oxygen" units="mmHg" ID="0"> <physical_parameter_set> <diffusion_coefficient units="micron^2/min">120000.0</diffusion_coefficient> <decay_rate units="1/min">0.1</decay_rate> </physical_parameter_set> <initial_condition units="mmHg">40.0</initial_condition> <Dirichlet_boundary_condition units="mmHg" enabled="true">42.7</Dirichlet_boundary_condition> </variable> <variable name="glucose" units="dimensionless" ID="1"> <physical_parameter_set> <diffusion_coefficient units="micron^2/min">18000.0</diffusion_coefficient> <decay_rate units="1/min">0.0</decay_rate> </physical_parameter_set> <initial_condition units="dimensionless">1</initial_condition> <Dirichlet_boundary_condition units="dimensionless" enabled="false">0</Dirichlet_boundary_condition> </variable> <options> <calculate_gradients>true</calculate_gradients> <track_internalized_substrates_in_each_agent>false</track_internalized_substrates_in_each_agent> <!-- not yet supported --> <initial_condition type="matlab" enabled="false"> <filename>./config/initial.mat</filename> </initial_condition> <!-- not yet supported --> <dirichlet_nodes type="matlab" enabled="false"> <filename>./config/dirichlet.mat</filename> </dirichlet_nodes> </options> </microenvironment_setup>
Controlling Dirichlet conditions on individual boundaries
In Version 1.7.0, we introduced the ability to control the Dirichlet conditions for each individual boundary for each substrate. The examples above apply (enable) or disable the same condition on each boundary with the same boundary value.
Suppose that we want to set glucose so that the Dirichlet condition is enabled on the bottom z boundary (with value 1) and the left and right x boundaries (with value 0.5) and disabled on all other boundaries. We modify the variable block by adding the optional Dirichlet_options block:
<variable name="glucose" units="dimensionless" ID="1"> <physical_parameter_set> <diffusion_coefficient units="micron^2/min">18000.0</diffusion_coefficient> <decay_rate units="1/min">0.0</decay_rate> </physical_parameter_set> <initial_condition units="dimensionless">1</initial_condition> <Dirichlet_boundary_condition units="dimensionless" enabled="true">0</Dirichlet_boundary_condition> <Dirichlet_options> <boundary_value ID="xmin" enabled="true">0.5</boundary_value> <boundary_value ID="xmax" enabled="true">0.5</boundary_value> <boundary_value ID="ymin" enabled="false">0.5</boundary_value> <boundary_value ID="ymin" enabled="false">0.5</boundary_value> <boundary_value ID="zmin" enabled="true">1.0</boundary_value> <boundary_value ID="zmax" enabled="false">0.5</boundary_value> </Dirichlet_options> </variable>
Notice a few things:
- The Dirichlet_boundary_condition element has its enabled attribute set to true
- The Dirichlet condition is set under any individual boundary with a boundary_value element.
- The ID attribute indicates which boundary is being specified.
- The enabled attribute allows the individual boundary to be enabled (with value given by the element’s value) or disabled (applying a Neumann or no-flux condition for this substrate at this boundary).
- Any individual boundary indicated by a boundary_value element supersedes the value given by Dirichlet_boundary_condition for this boundary.
Closing thoughts and future work
In the future, we plan to develop more of the options to allow users to set set the initial conditions externally and import them (via an external file), and to allow them to set up more complex domains by importing Dirichlet nodes.
More broadly, we are working to push more model specification from raw C++ to imported XML. It is our hope that this will vastly simplify model development, facilitate creation of graphical model editing tools, and ultimately broaden the class of developers who can use and contribute to PhysiCell. Thanks for giving it a try!
Building a Cellular Automaton Model Using BioFVM
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM. See below for guides to setting up a C++ compiler in Windows or OSX.
What you’ll need
- A working C++ development environment with support for OpenMP. See these prior tutorials if you need help.
- A download of BioFVM, available at http://BioFVM.MathCancer.org and http://BioFVM.sf.net. Use Version 1.1.4 or later.
- The source code for this project (see below).
Matlab or Octave for visualization. Matlab might be available for free at your university. Octave is open source and available from a variety of sources.
Our modeling task
We will implement a basic 3-D cellular automaton model of tumor growth in a well-mixed fluid, containing oxygen pO2 (mmHg) and a drug c (e.g., doxorubicin, μM), inspired by modeling by Alexander Anderson, Heiko Enderling, Jan Poleszczuk, Gibin Powathil, and others. (I highly suggest seeking out the sophisticated cellular automaton models at Moffitt’s Integrated Mathematical Oncology program!) This example shows you how to extend BioFVM into a new cellular automaton model. I’ll write a similar post on how to add BioFVM into an existing cellular automaton model, which you may already have available.
Tumor growth will be driven by oxygen availability. Tumor cells can be live, apoptotic (going through energy-dependent cell death, or necrotic (undergoing death from energy collapse). Drug exposure can both trigger apoptosis and inhibit cell cycling. We will model this as growth into a well-mixed fluid, with pO2 = 38 mmHg (about 5% oxygen: a physioxic value) and c = 5 μM.
Mathematical model
As a cellular automaton model, we will divide 3-D space into a regular lattice of voxels, with length, width, and height of 15 μm. (A typical breast cancer cell has radius around 9-10 μm, giving a typical volume around 3.6×103 μm3. If we make each lattice site have the volume of one cell, this gives an edge length around 15 μm.)
In voxels unoccupied by cells, we approximate a well-mixed fluid with Dirichlet nodes, setting pO2 = 38 mmHg, and initially setting c = 0. Whenever a cell dies, we replace it with an empty automaton, with no Dirichlet node. Oxygen and drug follow the typical diffusion-reaction equations:
\[ \frac{ \partial \textrm{pO}_2 }{\partial t} = D_\textrm{oxy} \nabla^2 \textrm{pO}_2 – \lambda_\textrm{oxy} \textrm{pO}_2 – \sum_{ \textrm{cells} i} U_{i,\textrm{oxy}} \textrm{pO}_2 \]
\[ \frac{ \partial c}{ \partial t } = D_c \nabla^2 c – \lambda_c c – \sum_{\textrm{cells }i} U_{i,c} c \]
where each uptake rate is applied across the cell’s volume. We start the treatment by setting c = 5 μM on all Dirichlet nodes at t = 504 hours (21 days). For simplicity, we do not model drug degradation (pharmacokinetics), to approximate the in vitro conditions.
In any time interval [t,t+Δt], each live tumor cell i has a probability pi,D of attempting division, probability pi,A of apoptotic death, and probability pi,N of necrotic death. (For simplicity, we ignore motility in this version.) We relate these to the birth rate bi, apoptotic death rate di,A, and necrotic death rate di,N by the linearized equations (from Macklin et al. 2012):
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes apoptotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,A}(t) \Delta t\Bigr) \approx d_{i,A}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ attempts division in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -b_i(t) \Delta t\Bigr) \approx b_{i}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes necrotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,N}(t) \Delta t\Bigr) \approx d_{i,N}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{dead cell } i \textrm{ lyses in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -\frac{1}{T_{i,D}} \Delta t\Bigr) \approx \frac{ \Delta t}{T_{i,D}} \]
(Illustrative) parameter values
We use Doxy = 105 μm2/min (Ghaffarizadeh et al. 2016), and we set Ui,oxy = 20 min-1 (to give an oxygen diffusion length scale of about 70 μm, with steeper gradients than our typical 100 μm length scale). We set λoxy = 0.01 min-1 for a 1 mm diffusion length scale in fluid.
We set Dc = 300 μm2/min, and Uc = 7.2×10-3 min-1 (Dc from Weinberg et al. (2007), and Ui,c twice as large as the reference value in Weinberg et al. (2007) to get a smaller diffusion length scale of about 204 μm). We set λc = 3.6×10-5 min-1 to give a drug diffusion length scale of about 2.9 mm in fluid.
We use TD = 8.6 hours for apoptotic cells, and TD = 60 days for necrotic cells (Macklin et al., 2013). However, note that necrotic and apoptotic cells lose volume quickly, so one may want to revise those time scales to match the point where a cell loses 90% of its volume.
Functional forms for the birth and death rates
We model pharmacodynamics with an area-under-the-curve (AUC) type formulation. If c(t) is the drug concentration at any cell i‘s location at time t, then let its integrated exposure Ei(t) be
\[ E_i(t) = \int_0^t c(s) \: ds \]
and we model its response with a Hill function
\[ R_i(t) = \frac{ E_i^h(t) }{ \alpha_i^h + E_i^h(t) }, \]
where h is the drug’s Hill exponent for the cell line, and α is the exposure for a half-maximum effect.
We model the microenvironment-dependent birth rate by:
\[ b_i(t) = \left\{ \begin{array}{lr} b_{i,P} \left( 1 – \eta_i R_i(t) \right) & \textrm{ if } \textrm{pO}_{2,P} < \textrm{pO}_2 \\ \\ b_{i,P} \left( \frac{\textrm{pO}_{2}-\textrm{pO}_{2,N}}{\textrm{pO}_{2,P}-\textrm{pO}_{2,N}}\right) \Bigl( 1 – \eta_i R_i(t) \Bigr) & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_2 \le \textrm{pO}_{2,P} \\ \\ 0 & \textrm{ if } \textrm{pO}_2 \le \textrm{pO}_{2,N}\end{array} \right. \]
where pO2,P is the physioxic oxygen value (38 mmHg), and pO2,N is a necrotic threshold (we use 5 mmHg), and 0 < η < 1 the drug’s birth inhibition. (A fully cytostatic drug has η = 1.)
We model the microenvironment-dependent apoptosis rate by:
\[ d_{i,A}(t) = d_{i,A}^* + \Bigl( d_{i,A}^\textrm{max} – d_{i,A}^* \Bigr) R_i(t) \]
\[ d_{i,N}(t) = \left\{ \begin{array}{lr} 0 & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_{2} \\ \\ d_{i,N}^* & \textrm{ if } \textrm{pO}_{2} \le \textrm{pO}_{2,N} \end{array}\right. \]
(Illustrative) parameter values
We use bi,P = 0.05 hour-1 (for a 20 hour cell cycle in physioxic conditions), di,A* = 0.01 bi,P, and di,N* = 0.04 hour-1 (so necrotic cells survive around 25 hours in low oxygen conditions).
We set α = 30 μM*hour (so that cells reach half max response after 6 hours’ exposure at a maximum concentration c = 5 μM), h = 2 (for a smooth effect), η = 0.25 (so that the drug is partly cytostatic), and di,Amax = 0.1 hour^-1 (so that cells survive about 10 hours after reaching maximum response).
Building the Cellular Automaton Model in BioFVM
BioFVM already includes Basic_Agents for cell-based substrate sources and sinks. We can extend these basic agents into full-fledged automata, and then arrange them in a lattice to create a full cellular automata model. Let’s sketch that out now.
Extending Basic_Agents to Automata
The main idea here is to define an Automaton class which extends (and therefore includes) the Basic_Agent class. This will give each Automaton full access to the microenvironment defined in BioFVM, including the ability to secrete and uptake substrates. We also make sure each Automaton “knows” which microenvironment it lives in (contains a pointer pMicroenvironment), and “knows” where it lives in the cellular automaton lattice. (More on that in the following paragraphs.)
So, as a schematic (just sketching out the most important members of the class):
class Standard_Data; // define per-cell biological data, such as phenotype,
// cell cycle status, etc..
class Custom_Data; // user-defined custom data, specific to a model.
class Automaton : public Basic_Agent
{
private:
Microenvironment* pMicroenvironment;
CA_Mesh* pCA_mesh;
int voxel_index;
protected:
public:
// neighbor connectivity information
std::vector<Automaton*> neighbors;
std::vector<double> neighbor_weights;
Standard_Data standard_data;
void (*current_state_rule)( Automaton& A , double );
Automaton();
void copy_parameters( Standard_Data& SD );
void overwrite_from_automaton( Automaton& A );
void set_cellular_automaton_mesh( CA_Mesh* pMesh );
CA_Mesh* get_cellular_automaton_mesh( void ) const;
void set_voxel_index( int );
int get_voxel_index( void ) const;
void set_microenvironment( Microenvironment* pME );
Microenvironment* get_microenvironment( void );
// standard state changes
bool attempt_division( void );
void become_apoptotic( void );
void become_necrotic( void );
void perform_lysis( void );
// things the user needs to define
Custom_Data custom_data;
// use this rule to add custom logic
void (*custom_rule)( Automaton& A , double);
};
So, the Automaton class includes everything in the Basic_Agent class, some Standard_Data (things like the cell state and phenotype, and per-cell settings), (user-defined) Custom_Data, basic cell behaviors like attempting division into an empty neighbor lattice site, and user-defined custom logic that can be applied to any automaton. To avoid lots of switch/case and if/then logic, each Automaton has a function pointer for its current activity (current_state_rule), which can be overwritten any time.
Each Automaton also has a list of neighbor Automata (their memory addresses), and weights for each of these neighbors. Thus, you can distance-weight the neighbors (so that corner elements are farther away), and very generalized neighbor models are possible (e.g., all lattice sites within a certain distance). When updating a cellular automaton model, such as to kill a cell, divide it, or move it, you leave the neighbor information alone, and copy/edit the information (standard_data, custom_data, current_state_rule, custom_rule). In many ways, an Automaton is just a bucket with a cell’s information in it.
Note that each Automaton also “knows” where it lives (pMicroenvironment and voxel_index), and knows what CA_Mesh it is attached to (more below).
Connecting Automata into a Lattice
An automaton by itself is lost in the world–it needs to link up into a lattice organization. Here’s where we define a CA_Mesh class, to hold the entire collection of Automata, setup functions (to match to the microenvironment), and two fundamental operations at the mesh level: copying automata (for cell division), and swapping them (for motility). We have provided two functions to accomplish these tasks, while automatically keeping the indexing and BioFVM functions correctly in sync. Here’s what it looks like:
class CA_Mesh{
private:
Microenvironment* pMicroenvironment;
Cartesian_Mesh* pMesh;
std::vector<Automaton> automata;
std::vector<int> iteration_order;
protected:
public:
CA_Mesh();
// setup to match a supplied microenvironment
void setup( Microenvironment& M );
// setup to match the default microenvironment
void setup( void );
int number_of_automata( void ) const;
void randomize_iteration_order( void );
void swap_automata( int i, int j );
void overwrite_automaton( int source_i, int destination_i );
// return the automaton sitting in the ith lattice site
Automaton& operator[]( int i );
// go through all nodes according to random shuffled order
void update_automata( double dt );
};
So, the CA_Mesh has a vector of Automata (which are never themselves moved), pointers to the microenvironment and its mesh, and a vector of automata indices that gives the iteration order (so that we can sample the automata in a random order). You can easily access an automaton with operator[], and copy the data from one Automaton to another with overwrite_automaton() (e.g, for cell division), and swap two Automata’s data (e.g., for cell migration) with swap_automata(). Finally, calling update_automata(dt) iterates through all the automata according to iteration_order, calls their current_state_rules and custom_rules, and advances the automata by dt.
Interfacing Automata with the BioFVM Microenvironment
The setup function ensures that the CA_Mesh is the same size as the Microenvironment.mesh, with same indexing, and that all automata have the correct volume, and dimension of uptake/secretion rates and parameters. If you declare and set up the Microenvironment first, all this is take care of just by declaring a CA_Mesh, as it seeks out the default microenvironment and sizes itself accordingly:
// declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // declare a Cellular_Automaton_Mesh CA_Mesh CA_model; // it's already good to go, initialized to empty automata: CA_model.display();
If you for some reason declare the CA_Mesh fist, you can set it up against the microenvironment:
// declare a CA_Mesh CA_Mesh CA_model; // declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // initialize the CA_Mesh to match the microenvironment CA_model.setup( M ); // it's already good to go, initialized to empty automata: CA_model.display();
Because each Automaton is in the microenvironment and inherits functions from Basic_Agent, it can secrete or uptake. For example, we can use functions like this one:
void set_uptake( Automaton& A, std::vector<double>& uptake_rates )
{
extern double BioFVM_CA_diffusion_dt;
// update the uptake_rates in the standard_data
A.standard_data.uptake_rates = uptake_rates;
// now, transfer them to the underlying Basic_Agent
*(A.uptake_rates) = A.standard_data.uptake_rates;
// and make sure the internal constants are self-consistent
A.set_internal_uptake_constants( BioFVM_CA_diffusion_dt );
}
A function acting on an automaton can sample the microenvironment to change parameters and state. For example:
void do_nothing( Automaton& A, double dt )
{ return; }
void microenvironment_based_rule( Automaton& A, double dt )
{
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// if pO2 < 5 mmHg, set the cell to a necrotic state
if( MS[0] < 5.0 ) { A.become_necrotic(); } // if drug > 5 uM, set the birth rate to zero
if( MS[1] > 5 )
{ A.standard_data.birth_rate = 0.0; }
// set the custom rule to something else
A.custom_rule = do_nothing;
return;
}
Implementing the mathematical model in this framework
We give each tumor cell a tumor_cell_rule (using this for custom_rule):
void viable_tumor_rule( Automaton& A, double dt )
{
// If there's no cell here, don't bother.
if( A.standard_data.state_code == BioFVM_CA_empty )
{ return; }
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// integrate drug exposure
A.standard_data.integrated_drug_exposure += ( MS[1]*dt );
A.standard_data.drug_response_function_value = pow( A.standard_data.integrated_drug_exposure,
A.standard_data.drug_hill_exponent );
double temp = pow( A.standard_data.drug_half_max_drug_exposure,
A.standard_data.drug_hill_exponent );
temp += A.standard_data.drug_response_function_value;
A.standard_data.drug_response_function_value /= temp;
// update birth rates (which themselves update probabilities)
update_birth_rate( A, MS, dt );
update_apoptotic_death_rate( A, MS, dt );
update_necrotic_death_rate( A, MS, dt );
return;
}
The functional tumor birth and death rates are implemented as:
void update_birth_rate( Automaton& A, std::vector<double>& MS, double dt )
{
static double O2_denominator = BioFVM_CA_physioxic_O2 - BioFVM_CA_necrotic_O2;
A.standard_data.birth_rate = A.standard_data.drug_response_function_value;
// response
A.standard_data.birth_rate *= A.standard_data.drug_max_birth_inhibition;
// inhibition*response;
A.standard_data.birth_rate *= -1.0;
// - inhibition*response
A.standard_data.birth_rate += 1.0;
// 1 - inhibition*response
A.standard_data.birth_rate *= viable_tumor_cell.birth_rate;
// birth_rate0*(1 - inhibition*response)
double temp1 = MS[0] ; // O2
temp1 -= BioFVM_CA_necrotic_O2;
temp1 /= O2_denominator;
A.standard_data.birth_rate *= temp1;
if( A.standard_data.birth_rate < 0 )
{ A.standard_data.birth_rate = 0.0; }
A.standard_data.probability_of_division = A.standard_data.birth_rate;
A.standard_data.probability_of_division *= dt;
// dt*birth_rate*(1 - inhibition*repsonse) // linearized probability
return;
}
void update_apoptotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.apoptotic_death_rate = A.standard_data.drug_max_death_rate;
// max_rate
A.standard_data.apoptotic_death_rate -= viable_tumor_cell.apoptotic_death_rate;
// max_rate - background_rate
A.standard_data.apoptotic_death_rate *= A.standard_data.drug_response_function_value;
// (max_rate-background_rate)*response
A.standard_data.apoptotic_death_rate += viable_tumor_cell.apoptotic_death_rate;
// background_rate + (max_rate-background_rate)*response
A.standard_data.probability_of_apoptotic_death = A.standard_data.apoptotic_death_rate;
A.standard_data.probability_of_apoptotic_death *= dt;
// dt*( background_rate + (max_rate-background_rate)*response ) // linearized probability
return;
}
void update_necrotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.necrotic_death_rate = 0.0;
A.standard_data.probability_of_necrotic_death = 0.0;
if( MS[0] > BioFVM_CA_necrotic_O2 )
{ return; }
A.standard_data.necrotic_death_rate = perinecrotic_tumor_cell.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death = A.standard_data.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death *= dt;
// dt*necrotic_death_rate
return;
}
And each fluid voxel (Dirichlet nodes) is implemented as the following (to turn on therapy at 21 days):
void fluid_rule( Automaton& A, double dt )
{
static double activation_time = 504;
static double activation_dose = 5.0;
static std::vector<double> activated_dirichlet( 2 , BioFVM_CA_physioxic_O2 );
static bool initialized = false;
if( !initialized )
{
activated_dirichlet[1] = activation_dose;
initialized = true;
}
if( fabs( BioFVM_CA_elapsed_time - activation_time ) < 0.01 ) { int ind = A.get_voxel_index(); if( A.get_microenvironment()->mesh.voxels[ind].is_Dirichlet )
{
A.get_microenvironment()->update_dirichlet_node( ind, activated_dirichlet );
}
}
}
At the start of the simulation, each non-cell automaton has its custom_rule set to fluid_rule, and each tumor cell Automaton has its custom_rule set to viable_tumor_rule. Here’s how:
void setup_cellular_automata_model( Microenvironment& M, CA_Mesh& CAM )
{
// Fill in this environment
double tumor_radius = 150;
double tumor_radius_squared = tumor_radius * tumor_radius;
std::vector<double> tumor_center( 3, 0.0 );
std::vector<double> dirichlet_value( 2 , 1.0 );
dirichlet_value[0] = 38; //physioxia
dirichlet_value[1] = 0; // drug
for( int i=0 ; i < M.number_of_voxels() ;i++ )
{
std::vector<double> displacement( 3, 0.0 );
displacement = M.mesh.voxels[i].center;
displacement -= tumor_center;
double r2 = norm_squared( displacement );
if( r2 > tumor_radius_squared ) // well_mixed_fluid
{
M.add_dirichlet_node( i, dirichlet_value );
CAM[i].copy_parameters( well_mixed_fluid );
CAM[i].custom_rule = fluid_rule;
CAM[i].current_state_rule = do_nothing;
}
else // tumor
{
CAM[i].copy_parameters( viable_tumor_cell );
CAM[i].custom_rule = viable_tumor_rule;
CAM[i].current_state_rule = advance_live_state;
}
}
}
Overall program loop
There are two inherent time scales in this problem: cell processes like division and death (happen on the scale of hours), and transport (happens on the order of minutes). We take advantage of this by defining two step sizes:
double BioFVM_CA_dt = 3; std::string BioFVM_CA_time_units = "hr"; double BioFVM_CA_save_interval = 12; double BioFVM_CA_max_time = 24*28; double BioFVM_CA_elapsed_time = 0.0; double BioFVM_CA_diffusion_dt = 0.05; std::string BioFVM_CA_transport_time_units = "min"; double BioFVM_CA_diffusion_max_time = 5.0;
Every time the simulation advances by BioFVM_CA_dt (on the order of hours), we run diffusion to quasi-steady state (for BioFVM_CA_diffusion_max_time, on the order of minutes), using time steps of size BioFVM_CA_diffusion time. We performed numerical stability and convergence analyses to determine 0.05 min works pretty well for regular lattice arrangements of cells, but you should always perform your own testing!
Here’s how it all looks, in a main program loop:
BioFVM_CA_elapsed_time = 0.0;
double next_output_time = BioFVM_CA_elapsed_time; // next time you save data
while( BioFVM_CA_elapsed_time < BioFVM_CA_max_time + 1e-10 )
{
// if it's time, save the simulation
if( fabs( BioFVM_CA_elapsed_time - next_output_time ) < BioFVM_CA_dt/2.0 )
{
std::cout << "simulation time: " << BioFVM_CA_elapsed_time << " " << BioFVM_CA_time_units
<< " (" << BioFVM_CA_max_time << " " << BioFVM_CA_time_units << " max)" << std::endl;
char* filename;
filename = new char [1024];
sprintf( filename, "output_%6f" , next_output_time );
save_BioFVM_cellular_automata_to_MultiCellDS_xml_pugi( filename , M , CA_model ,
BioFVM_CA_elapsed_time );
cell_counts( CA_model );
delete [] filename;
next_output_time += BioFVM_CA_save_interval;
}
// do the cellular automaton step
CA_model.update_automata( BioFVM_CA_dt );
BioFVM_CA_elapsed_time += BioFVM_CA_dt;
// simulate biotransport to quasi-steady state
double t_diffusion = 0.0;
while( t_diffusion < BioFVM_CA_diffusion_max_time + 1e-10 )
{
M.simulate_diffusion_decay( BioFVM_CA_diffusion_dt );
M.simulate_cell_sources_and_sinks( BioFVM_CA_diffusion_dt );
t_diffusion += BioFVM_CA_diffusion_dt;
}
}
Getting and Running the Code
- Start a project: Create a new directory for your project (I’d recommend “BioFVM_CA_tumor”), and enter the directory. Place a copy of BioFVM (the zip file) into your directory. Unzip BioFVM, and copy BioFVM*.h, BioFVM*.cpp, and pugixml* files into that directory.
- Download the demo source code: Download the source code for this tutorial: BioFVM_CA_Example_1, version 1.0.0 or later. Unzip its contents into your project directory. Go ahead and overwrite the Makefile.
- Edit the makefile (if needed): Note that if you are using OSX, you’ll probably need to change from “g++” to your installed compiler. See these tutorials.
- Test the code: Go to a command line (see previous tutorials), and test:
make ./BioFVM_CA_Example_1
(If you’re on windows, run BioFVM_CA_Example_1.exe.)
Simulation Result
If you run the code to completion, you will simulate 3 weeks of in vitro growth, followed by a bolus “injection” of drug. The code will simulate one one additional week under the drug. (This should take 5-10 minutes, including full simulation saves every 12 hours.)
In matlab, you can load a saved dataset and check the minimum oxygenation value like this:
MCDS = read_MultiCellDS_xml( 'output_504.000000.xml' ); min(min(min( MCDS.continuum_variables(1).data )))
And then you can start visualizing like this:
contourf( MCDS.mesh.X_coordinates , MCDS.mesh.Y_coordinates , ...
MCDS.continuum_variables(1).data(:,:,33)' ) ;
axis image;
colorbar
xlabel('x (\mum)' , 'fontsize' , 12 );
ylabel( 'y (\mum)' , 'fontsize', 12 );
set(gca, 'fontsize', 12 );
title('Oxygenation (mmHg) at z = 0 \mum', 'fontsize', 14 );
print('-dpng', 'Tumor_o2_3_weeks.png' );
plot_cellular_automata( MCDS , 'Tumor spheroid at 3 weeks');
Simulation plots
Here are some plots, showing (left from right) pO2 concentration, a cross-section of the tumor (red = live cells, green = apoptotic, and blue = necrotic), and the drug concentration (after start of therapy):
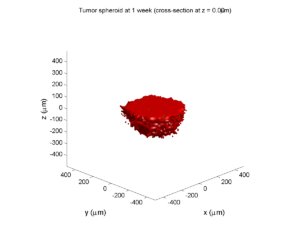
1 week:
Oxygen- and space-limited growth are restricted to the outer boundary of the tumor spheroid.
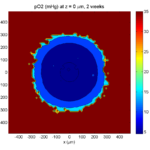
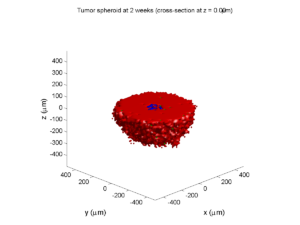
2 weeks:
Oxygenation is dipped below 5 mmHg in the center, leading to necrosis.
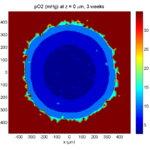
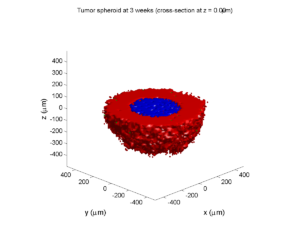
3 weeks:
As the tumor grows, the hypoxic gradient increases, and the necrotic core grows. The code turns on a constant 5 micromolar dose of doxorubicin at this point
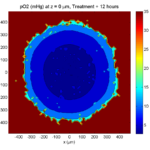
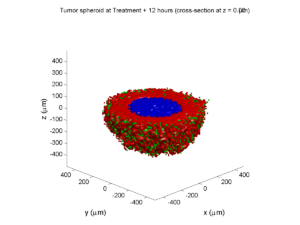
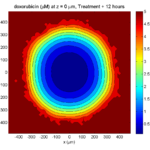
Treatment + 12 hours:
The drug has started to penetrate the tumor, triggering apoptotic death towards the outer periphery where exposure has been greatest.
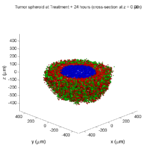
Treatment + 24 hours:
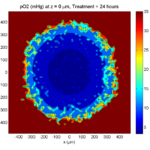
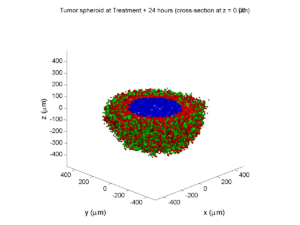
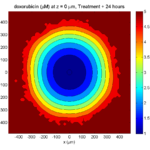
The drug profile hasn’t changed much, but the interior cells have now had greater exposure to drug, and hence greater response. Now apoptosis is observed throughout the non-necrotic tumor. The tumor has decreased in volume somewhat.
Treatment + 36 hours:
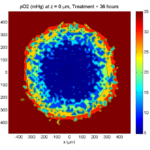
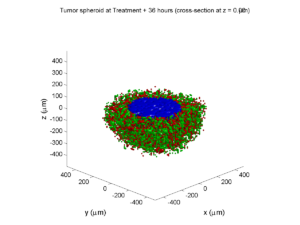
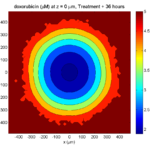
The non-necrotic tumor is now substantially apoptotic. We would require some pharamcokinetic effects (e.g., drug clearance, inactivation, or removal) to avoid the inevitable, presences of a pre-existing resistant strain, or emergence of resistance.
Treatment + 48 hours:
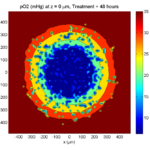
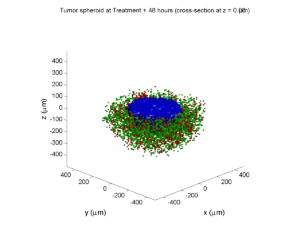
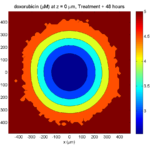
By now, almost all cells are apoptotic.
Treatment + 60 hours:

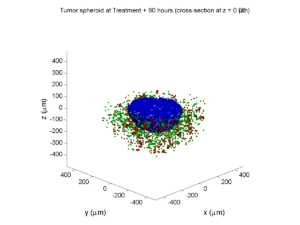
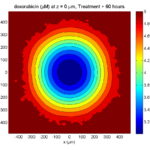
The non-necrotic tumor is nearly completed eliminated, leaving a leftover core of previously-necrotic cells (which did not change state in response to the drug–they were already dead!)
Source files
You can download completed source for this example here: https://sourceforge.net/projects/biofvm/files/Tutorials/Cellular_Automaton_1/
This file will include the following:
- BioFVM_cellular_automata.h
- BioFVM_cellular_automata.cpp
- BioFVM_CA_example_1.cpp
- read_MultiCellDS_xml.m (updated)
- plot_cellular_automata.m
- Makefile
What’s next
I plan to update this source code with extra cell motility, and potentially more realistic parameter values. Also, I plan to more formally separate out the example from the generic cell capabilities, so that this source code can work as a bona fide cellular automaton framework.
More immediately, my next tutorial will use the reverse strategy: start with an existing cellular automaton model, and integrate BioFVM capabilities.
Return to News • Return to MathCancer • Follow @MathCancer
BioFVM warmup: 2D continuum simulation of tumor growth
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM. See also the guides to setting up a C++ compiler in Windows or OSX.
What you’ll need
- A working C++ development environment with support for OpenMP. See these prior tutorials if you need help.
- A download of BioFVM, available at http://BioFVM.MathCancer.org and http://BioFVM.sf.net. Use Version 1.0.3 or later.
- Matlab or Octave for visualization. Matlab might be available for free at your university. Octave is open source and available from a variety of sources.
Our modeling task
We will implement a basic 2-D model of tumor growth in a heterogeneous microenvironment, with inspiration by glioblastoma models by Kristin Swanson, Russell Rockne and others (e.g., this work), and continuum tumor growth models by Hermann Frieboes, John Lowengrub, and our own lab (e.g., this paper and this paper).
We will model tumor growth driven by a growth substrate, where cells die when the growth substrate is insufficient. The tumor cells will have motility. A continuum blood vasculature will supply the growth substrate, but tumor cells can degrade this existing vasculature. We will revisit and extend this model from time to time in future tutorials.
Mathematical model
Taking inspiration from the groups mentioned above, we’ll model a live cell density ρ of a relatively low-adhesion tumor cell species (e.g., glioblastoma multiforme). We’ll assume that tumor cells move randomly towards regions of low cell density (modeled as diffusion with motility μ). We’ll assume that that the net birth rate rB is proportional to the concentration of growth substrate σ, which is released by blood vasculature with density b. Tumor cells can degrade the tissue and hence this existing vasculature. Tumor cells die at rate rD when the growth substrate level is too low. We assume that the tumor cell density cannot exceed a max level ρmax. A model that includes these effects is:
\[ \frac{ \partial \rho}{\partial t} = \mu \nabla^2 \rho + r_B(\sigma)\rho \left( 1 – \frac{ \rho}{\rho_\textrm{max}} \right) – r_D(\sigma) \rho \]
\[ \frac{ \partial b}{\partial t} = – r_\textrm{degrade} \rho b \]
\[ \frac{\partial \sigma}{ \partial t} = D\nabla^2 \sigma – \lambda_a \sigma – \lambda_2 \rho \sigma + r_\textrm{deliv}b \left( \sigma_\textrm{max} – \sigma \right) \]
where for the birth and death rates, we’ll use the constitutive relations:
\[ r_B(\sigma) = r_B \textrm{ max} \left( \frac{\sigma – \sigma_\textrm{min}}{ \sigma_\textrm{ max} – \sigma_\textrm{min} } , 0 \right)\]
\[r_D(\sigma) = r_D \textrm{ max} \left( \frac{ \sigma_\textrm{min} – \sigma}{\sigma_\textrm{min}} , 0 \right) \]
Mapping the model onto BioFVM
BioFVM solves on a vector u of substrates. We’ll set u = [ρ , b, σ ]. The code expects PDEs of the general form:
\[ \frac{\partial q}{\partial t} = D\nabla^2 q – \lambda q + S\left( q^* – q \right) – Uq\]
So, we determine the decay rate (λ), source function (S), and uptake function (U) for the cell density ρ and the growth substrate σ.
Cell density
We first slightly rewrite the PDE:
\[ \frac{ \partial \rho}{\partial t} = \mu \nabla^2 \rho + r_B(\sigma) \frac{ \rho}{\rho_\textrm{max}} \left( \rho_\textrm{max} – \rho \right) – r_D(\sigma)\rho \]
and then try to match to the general form term-by-term. While BioFVM wasn’t intended for solving nonlinear PDEs of this form, we can make it work by quasi-linearizing, with the following functions:
\[ S = r_B(\sigma) \frac{ \rho }{\rho_\textrm{max}} \hspace{1in} U = r_D(\sigma). \]
When implementing this, we’ll evaluate σ and ρ at the previous time step. The diffusion coefficient is μ, and the decay rate is zero. The target or saturation density is ρmax.
Growth substrate
Similarly, by matching the PDE for σ term-by-term with the general form, we use:
\[ S = r_\textrm{deliv}b, \hspace{1in} U = \lambda_2 \rho. \]
The diffusion coefficient is D, the decay rate is λ1, and the saturation density is σmax.
Blood vessels
Lastly, a term-by-term matching of the blood vessel equation gives the following functions:
\[ S=0 \hspace{1in} U = r_\textrm{degrade}\rho. \]
The diffusion coefficient, decay rate, and saturation density are all zero.
Implementation in BioFVM
- Start a project: Create a new directory for your project (I’d recommend “BioFVM_2D_tumor”), and enter the directory. Place a copy of BioFVM (the zip file) into your directory. Unzip BioFVM, and copy BioFVM*.h, BioFVM*.cpp, and pugixml* files into that directory.
- Copy the matlab visualization files: To help read and plot BioFVM data, we have provided matlab files. Copy all the *.m files from the matlab subdirectory to your project.
- Copy the empty project: BioFVM Version 1.0.3 or later includes a template project and Makefile to make it easier to get started. Copy the Makefile and template_project.cpp file to your project. Rename template_project.cpp to something useful, like 2D_tumor_example.cpp.
- Edit the makefile: Open a terminal window and browse to your project. Tailor the makefile to your new project:
notepad++ Makefile
Change the PROGRAM_NAME to 2Dtumor.
Also, rename main to 2D_tumor_example throughout the Makefile.
Lastly, note that if you are using OSX, you’ll probably need to change from “g++” to your installed compiler. See these tutorials.
- Start adapting 2D_tumor_example.cpp: First, open 2D_tumor_example.cpp:
notepad++ 2D_tumor_example.cpp
Just after the “using namespace BioFVM” section of the code, define useful globals. Here and throughout, new and/or modified code is in blue:
using namespace BioFVM: // helpful -- have indices for each "species" int live_cells = 0; int blood_vessels = 1; int oxygen = 2; // some globals double prolif_rate = 1.0 /24.0; double death_rate = 1.0 / 6; // double cell_motility = 50.0 / 365.25 / 24.0 ; // 50 mm^2 / year --> mm^2 / hour double o2_uptake_rate = 3.673 * 60.0; // 165 micron length scale double vessel_degradation_rate = 1.0 / 2.0 / 24.0 ; // 2 days to disrupt tissue double max_cell_density = 1.0; double o2_supply_rate = 10.0; double o2_normoxic = 1.0; double o2_hypoxic = 0.2;
- Set up the microenvironment: Within main(), make sure we have the right number of substrates, and set them up:
// create a microenvironment, and set units Microenvironment M; M.name = "Tumor microenvironment"; M.time_units = "hr"; M.spatial_units = "mm"; M.mesh.units = M.spatial_units; // set up and add all the densities you plan M.set_density( 0 , "live cells" , "cells" ); M.add_density( "blood vessels" , "vessels/mm^2" ); M.add_density( "oxygen" , "cells" ); // set the properties of the diffusing substrates M.diffusion_coefficients[live_cells] = cell_motility; M.diffusion_coefficients[blood_vessels] = 0; M.diffusion_coefficients[oxygen] = 6.0; // 1e5 microns^2/min in units mm^2 / hr M.decay_rates[live_cells] = 0; M.decay_rates[blood_vessels] = 0; M.decay_rates[oxygen] = 0.01 * o2_uptake_rate; // 1650 micron length scale
Notice how our earlier global definitions of “live_cells”, “blood_vessels”, and “oxygen” makes it easier to make sure we’re referencing the correct substrates in lines like these.
- Resize the domain and test: For this example (and so the code runs very quickly), we’ll work in 2D in a 2 cm × 2 cm domain:
// set the mesh size double dx = 0.05; // 50 microns M.resize_space( 0.0 , 20.0 , 0, 20.0 , -dx/2.0, dx/2.0 , dx, dx, dx );
Notice that we use a tissue thickness of dx/2 to use the 3D code for a 2D simulation. Now, let’s test:
make 2Dtumor
Go ahead and cancel the simulation [Control]+C after a few seconds. You should see something like this:
Starting program ... Microenvironment summary: Tumor microenvironment: Mesh information: type: uniform Cartesian Domain: [0,20] mm x [0,20] mm x [-0.025,0.025] mm resolution: dx = 0.05 mm voxels: 160000 voxel faces: 0 volume: 20 cubic mm Densities: (3 total) live cells: units: cells diffusion coefficient: 0.00570386 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 75523.9 mm blood vessels: units: vessels/mm^2 diffusion coefficient: 0 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 0 mm oxygen: units: cells diffusion coefficient: 6 mm^2 / hr decay rate: 2.2038 hr^-1 diffusion length scale: 1.65002 mm simulation time: 0 hr (100 hr max) Using method diffusion_decay_solver__constant_coefficients_LOD_3D (implicit 3-D LOD with Thomas Algorithm) ... simulation time: 10 hr (100 hr max) simulation time: 20 hr (100 hr max)
- Set up initial conditions: We’re going to make a small central focus of tumor cells, and a “bumpy” field of blood vessels.
// set initial conditions // use this syntax to create a zero vector of length 3 // std::vector<double> zero(3,0.0); std::vector<double> center(3); center[0] = M.mesh.x_coordinates[M.mesh.x_coordinates.size()-1] /2.0; center[1] = M.mesh.y_coordinates[M.mesh.y_coordinates.size()-1] /2.0; center[2] = 0; double radius = 1.0; std::vector<double> one( M.density_vector(0).size() , 1.0 ); double pi = 2.0 * asin( 1.0 ); // use this syntax for a parallelized loop over all the // voxels in your mesh: #pragma omp parallel for for( int i=0; i < M.number_of_voxels() ; i++ ) { std::vector<double> displacement = M.voxels(i).center – center; double distance = norm( displacement ); if( distance < radius ) { M.density_vector(i)[live_cells] = 0.1; } M.density_vector(i)[blood_vessels]= 0.5 + 0.5*cos(0.4* pi * M.voxels(i).center[0])*cos(0.3*pi *M.voxels(i).center[1]); M.density_vector(i)[oxygen] = o2_normoxic; } - Change to a 2D diffusion solver:
// set up the diffusion solver, sources and sinks M.diffusion_decay_solver = diffusion_decay_solver__constant_coefficients_LOD_2D;
- Set the simulation times: We’ll simulate 10 days, with output every 12 hours.
double t = 0.0; double t_max = 10.0 * 24.0; // 10 days double dt = 0.1; double output_interval = 12.0; // how often you save data double next_output_time = t; // next time you save data
- Set up the source function:
void supply_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] static double temp1 = prolif_rate / ( o2_normoxic – o2_hypoxic ); (*write_here)[live_cells] = microenvironment->density_vector(voxel_index)[oxygen]; (*write_here)[live_cells] -= o2_hypoxic; if( (*write_here)[live_cells] < 0.0 ) { (*write_here)[live_cells] = 0.0; } else { (*write_here)[live_cells] = temp1; (*write_here)[live_cells] *= microenvironment->density_vector(voxel_index)[live_cells]; } (*write_here)[blood_vessels] = 0.0; (*write_here)[oxygen] = o2_supply_rate; (*write_here)[oxygen] *= microenvironment->density_vector(voxel_index)[blood_vessels]; return; }Notice the use of the static internal variable temp1: the first time this function is called, it declares this helper variable (to save some multiplication operations down the road). The static variable is available to all subsequent calls of this function.
- Set up the target function (substrate saturation densities):
void supply_target_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] (*write_here)[live_cells] = max_cell_density; (*write_here)[blood_vessels] = 1.0; (*write_here)[oxygen] = o2_normoxic; return; } - Set up the uptake function:
void uptake_function( Microenvironment* microenvironment, int voxel_index, std::vector<double>* write_here ) { // use this syntax to access the jth substrate write_here // (*write_here)[j] // use this syntax to access the jth substrate in voxel voxel_index of microenvironment: // microenvironment->density_vector(voxel_index)[j] (*write_here)[live_cells] = o2_hypoxic; (*write_here)[live_cells] -= microenvironment->density_vector(voxel_index)[oxygen]; if( (*write_here)[live_cells] < 0.0 ) { (*write_here)[live_cells] = 0.0; } else { (*write_here)[live_cells] *= death_rate; } (*write_here)[oxygen] = o2_uptake_rate ; (*write_here)[oxygen] *= microenvironment->density_vector(voxel_index)[live_cells]; (*write_here)[blood_vessels] = vessel_degradation_rate ; (*write_here)[blood_vessels] *= microenvironment->density_vector(voxel_index)[live_cells]; return; }
And that’s it. The source should be ready to go!
Source files
You can download completed source for this example here:
Using the code
Running the code
First, compile and run the code:
make 2Dtumor
The output should look like this.
Starting program … Microenvironment summary: Tumor microenvironment: Mesh information: type: uniform Cartesian Domain: [0,20] mm x [0,20] mm x [-0.025,0.025] mm resolution: dx = 0.05 mm voxels: 160000 voxel faces: 0 volume: 20 cubic mm Densities: (3 total) live cells: units: cells diffusion coefficient: 0.00570386 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 75523.9 mm blood vessels: units: vessels/mm^2 diffusion coefficient: 0 mm^2 / hr decay rate: 0 hr^-1 diffusion length scale: 0 mm oxygen: units: cells diffusion coefficient: 6 mm^2 / hr decay rate: 2.2038 hr^-1 diffusion length scale: 1.65002 mm simulation time: 0 hr (240 hr max) Using method diffusion_decay_solver__constant_coefficients_LOD_2D (2D LOD with Thomas Algorithm) … simulation time: 12 hr (240 hr max) simulation time: 24 hr (240 hr max) simulation time: 36 hr (240 hr max) simulation time: 48 hr (240 hr max) simulation time: 60 hr (240 hr max) simulation time: 72 hr (240 hr max) simulation time: 84 hr (240 hr max) simulation time: 96 hr (240 hr max) simulation time: 108 hr (240 hr max) simulation time: 120 hr (240 hr max) simulation time: 132 hr (240 hr max) simulation time: 144 hr (240 hr max) simulation time: 156 hr (240 hr max) simulation time: 168 hr (240 hr max) simulation time: 180 hr (240 hr max) simulation time: 192 hr (240 hr max) simulation time: 204 hr (240 hr max) simulation time: 216 hr (240 hr max) simulation time: 228 hr (240 hr max) simulation time: 240 hr (240 hr max) Done!
Looking at the data
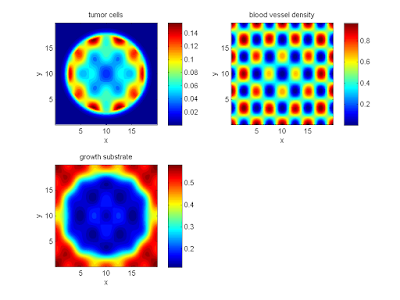
Now, let’s pop it open in matlab (or octave):
matlab
To load and plot a single time (e.g., the last tim)
!ls *.mat M = read_microenvironment( 'output_240.000000.mat' ); plot_microenvironment( M );
To add some labels:
labels{1} = 'tumor cells';
labels{2} = 'blood vessel density';
labels{3} = 'growth substrate';
plot_microenvironment( M ,labels );
Your output should look a bit like this:
Lastly, you might want to script the code to create and save plots of all the times.
labels{1} = 'tumor cells';
labels{2} = 'blood vessel density';
labels{3} = 'growth substrate';
for i=0:20
t = i*12;
input_file = sprintf( 'output_%3.6f.mat', t );
output_file = sprintf( 'output_%3.6f.png', t );
M = read_microenvironment( input_file );
plot_microenvironment( M , labels );
print( gcf , '-dpng' , output_file );
end
What’s next
We’ll continue posting new tutorials on adapting BioFVM to existing and new simulators, as well as guides to new features as we roll them out.
Stay tuned and watch this blog!
BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations
I’m very excited to announce that our 3-D diffusion solver has been accepted for publication and is now online at Bioinformatics. Click here to check out the open access preprint!
A. Ghaffarizadeh, S.H. Friedman, and P. Macklin. BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations. Bioinformatics, 2015.
DOI: 10.1093/bioinformatics/btv730 (free; open access)
BioFVM (stands for “Finite Volume Method for biological problems) is an open source package to solve for 3-D diffusion of several substrates with desktop workstations, single supercomputer nodes, or even laptops (for smaller problems). We built it from the ground up for biological problems, with optimizations in C++ and OpenMP to take advantage of all those cores on your CPU. The code is available at SourceForge and BioFVM.MathCancer.org.
The main idea here is to make it easier to simulate big, cool problems in 3-D multicellular biology. We’ll take care of secretion, diffusion, and uptake of things like oxygen, glucose, metabolic waste products, signaling factors, and drugs, so you can focus on the rest of your model.
Design philosophy and main capabilities
Solving diffusion equations efficiently and accurately is hard, especially in 3D. Almost all biological simulations deal with this, many by using explicit finite differences (easy to code and accurate, but very slow!) or implicit methods like ADI (accurate and relatively fast, but difficult to code with complex linking to libraries). While real biological systems often depend upon many diffusing things (lots of signaling factors for cell-cell communication, growth substrates, drugs, etc.), most solvers only scale well to simulating two or three. We solve a system of PDEs of the following form:
\[ \frac{\partial \vec{\rho}}{\partial t} = \overbrace{ \vec{D} \nabla^2 \vec{\rho} }^\textrm{diffusion}
– \overbrace{ \vec{\lambda} \vec{\rho} }^\textrm{decay} + \overbrace{ \vec{S} \left( \vec{\rho}^* – \vec{\rho} \right) }^{\textrm{bulk source}} – \overbrace{ \vec{U} \vec{\rho} }^{\textrm{bulk uptake}} + \overbrace{\sum_{\textrm{cells } k} 1_k(\vec{x}) \left[ \vec{S}_k \left( \vec{\rho}^*_k – \vec{\rho} \right) – \vec{U}_k \vec{\rho} \right] }^\textrm{sources and sinks by cells} \]
Above, all vector-vector products are term-by-term.
Solving for many diffusing substrates
We set out to write a package that could simulate many diffusing substrates using algorithms that were fast but simple enough to optimize. To do this, we wrote the entire solver to work on vectors of substrates, rather than on individual PDEs. In performance testing, we found that simulating 10 diffusing things only takes about 2.6 times longer than simulating one. (In traditional codes, simulating ten things takes ten times as long as simulating one.) We tried our hardest to break the code in our testing, but we failed. We simulated all the way from 1 diffusing substrate up to 128 without any problems. Adding new substrates increases the computational cost linearly.
Combining simple but tailored solvers
We used an approach called operator splitting: breaking a complicated PDE into a series of simpler PDEs and ODEs, which can be solved one at a time with implicit methods. This allowed us to write a very fast diffusion/decay solver, a bulk supply/uptake solver, and a cell-based secretion/uptake solver. Each of these individual solvers was individually optimized. Theory tells us that if each individual solver is first-order accurate in time and stable, then the overall approach is first-order accurate in time and stable.
The beauty of the approach is that each solver can individually be improved over time. For example, in BioFVM 1.0.2, we doubled the performance of the cell-based secretion/uptake solver. The operator splitting approach also lets us add new terms to the “main” PDE by writing new solvers, rather than rewriting a large, monolithic solver. We will take advantage of this to add advective terms (critical for interstitial flow) in future releases.
Optimizing the diffusion solver for large 3-D domains
For the first main release of BioFVM, we restricted ourselves to Cartesian meshes, which allowed us to write very tailored mesh data structures and diffusion solvers. (Note: the finite volume method reduces to finite differences on Cartesian meshes with trivial Neumann boundary conditions.) We intend to work on more general Voronoi meshes in a future release. (This will be particularly helpful for sources/sinks along blood vessels.)
By using constant diffusion and decay coefficients, we were able to write very fast solvers for Cartesian meshes. We use the locally one-dimensional (LOD) method–a specialized form of operator splitting–to break the 3-D diffusion problem into a series of 1-D diffusion problems. For each (y,z) in our mesh, we have a 1-D diffusion problem along x. This yields a tridiagonal linear system which we can solve efficiently with the Thomas algorithm. Moreover, because the forward-sweep steps only depend upon the coefficient matrix (which is unchanging over time), we can pre-compute and store the results in memory for all the x-diffusion problems. In fact, the structure of the matrix allows us to pre-compute part of the back-substitution steps as well. Same for y- and z-diffusion. This gives a big speedup.
Next, we can use all those CPU cores to speed up our work. While the back-substitution steps of the Thomas algorithm can’t be easily parallelized (it’s a serial operation), we can solve many x-diffusion problems at the same time, using independent copies (instances) of the Thomas solver. So, we break up all the x-diffusion problems up across a big OpenMP loop, and repeat for y– and z-diffusion.
Lastly, we used overloaded +=, axpy and similar operations on the vector of substrates, to avoid unnecessary (and very expensive) memory allocation and copy operations wherever we could. This was a really fun code to write!
The work seems to have payed off: we have found that solving on 1 million voxel meshes (about 8 mm3 at 20 μm resolution) is easy even for laptops.
Simulating many cells
We tailored the solver to allow both lattice- and off-lattice cell sources and sinks. Desktop workstations should have no trouble with 1,000,000 cells secreting and uptaking a few substrates.
Simplifying the non-science
We worked to minimize external dependencies, because few things are more frustrating than tracking down a bunch of libraries that may not work together on your platform. The first release BioFVM only has one external dependency: pugixml (an XML parser). We didn’t link an entire linear algebra library just to get axpy and a Thomas solver–it wouldn’t have been optimized for our system anyway. We implemented what we needed of the freely available .mat file specification, rather than requiring a separate library for that. (We have used these matlab read/write routines in house for several years.)
Similarly, we stuck to a very simple mesh data structure so we wouldn’t have to maintain compatibility with general mesh libraries (which can tend to favor feature sets and generality over performance and simplicity). Rather than use general-purpose ODE solvers (with yet more library dependencies, and more work for maintaining compatibility), we wrote simple solvers tailored specifically to our equations.
The upshot of this is that you don’t have to do anything fancy to replicate results with BioFVM. Just grab a copy of the source, drop it into your project directory, include it in your project (e.g., your makefile), and you’re good to go.
All the juicy details
The Bioinformatics paper is just 2 pages long, using the standard “Applications Note” format. It’s a fantastic format for announcing and disseminating a piece of code, and we’re grateful to be published there. But you should pop open the supplementary materials, because all the fun mathematics are there:
- The full details of the numerical algorithm, including information on our optimizations.
- Convergence tests: For several examples, we showed:
- First-order convergence in time (with respect to Δt), and stability
- Second-order convergence in space (with respect to Δx)
- Accuracy tests: For each convergence test, we looked at how small Δt has to be to ensure 5% relative accuracy at Δx = 20 μm resolution. For oxygen-like problems with cell-based sources and sinks, Δt = 0.01 min will do the trick. This is about 15 times larger than the stability-restricted time step for explicit methods.
- Performance tests:
- Computational cost (wall time to simulate a fixed problem on a fixed domain size with fixed time/spatial resolution) increases linearly with the number of substrates. 5-10 substrates are very feasible on desktop workstations.
- Computational cost increases linearly with the number of voxels
- Computational cost increases linearly in the number of cell-based source/sinks
And of course because this code is open sourced, you can dig through the implementation details all you like! (And improvements are welcome!)
What’s next?
- As MultiCellDS (multicellular data standard) matures, we will implement read/write support for <microenvironment> data in digital snapshots.
- We have a few ideas to improve the speed of the cell-based sources and sinks. In particular, switching to a higher-order accurate solver may allow larger time step sizes, so long as the method is still stable. For the specific form of the sources/sinks, the trapezoid rule could work well here.
- I’d like to allow a spatially-varying diffusion coefficient. We could probably do this (at very great memory cost) by writing separate Thomas solvers for each strip in x, y, and z, or by giving up the pre-computation part of the optimization. I’m still mulling this one over.
- I’d also like to implement non-Cartesian meshes. The data structure isn’t a big deal, but we lose the LOD optimization and Thomas solvers. In this case, we’d either use explicit methods (very slow!), use an iterative matrix solver (trickier to parallelize nicely, except in matrix-vector multiplication operations), or start with quasi-steady problems that let us use Gauss-Seidel iterative type methods, like this old paper.
- Since advective flow (particularly interstitial flow) is so important for many problems, I’d like to add an advective solver. This will require some sort of upwinding to maintain stability.
- At some point, we’d like to port this to GPUs. However, I don’t currently have time / resources to maintain a separate CUDA or OpenCL branch. (Perhaps this will be an excuse to learn Julia on GPUs.)
Well, we hope you find BioFVM useful. If you give it a shot, I’d love to hear back from you!
Very best — Paul