Category: 3D
PhysiCell Tools : PhysiCell-povwriter
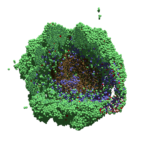
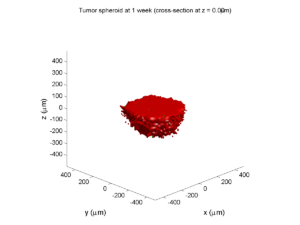
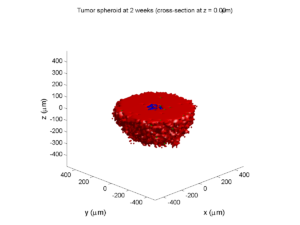
As PhysiCell matures, we are starting to turn our attention to better training materials and an ecosystem of open source PhysiCell tools. PhysiCell-povwriter is is designed to help transform your 3-D simulation results into 3-D visualizations like this one:
PhysiCell-povwriter transforms simulation snapshots into 3-D scenes that can be rendered into still images using POV-ray: an open source software package that uses raytracing to mimic the path of light from a source of illumination to a single viewpoint (a camera or an eye). The result is a beautifully rendered scene (at any resolution you choose) with very nice shading and lighting.
If you repeat this on many simulation snapshots, you can create an animation of your work.
What you’ll need
This workflow is entirely based on open source software:
- 3-D simulation data (likely stored in ./output from your project)
- PhysiCell-povwriter, available on GitHub at
- POV-ray, available at
- ImageMagick (optional, for image file conversions)
- mencoder (optional, for making compressed movies)
Setup
Building PhysiCell-povwriter
After you clone PhysiCell-povwriter or download its source from a release, you’ll need to compile it. In the project’s root directory, compile the project by:
make
(If you need to set up a C++ PhysiCell development environment, click here for OSX or here for Windows.)
Next, copy povwriter (povwriter.exe in Windows) to either the root directory of your PhysiCell project, or somewhere in your path. Copy ./config/povwriter-settings.xml to the ./config directory of your PhysiCell project.
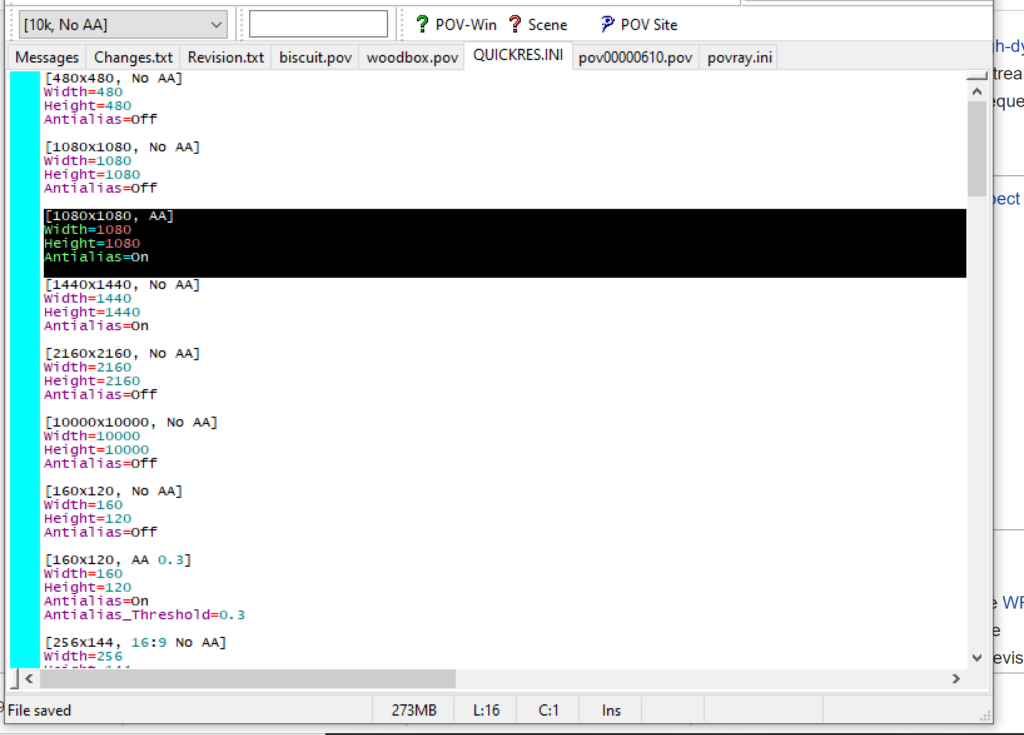
Editing resolutions in POV-ray
PhysiCell-povwriter is intended for creating “square” images, but POV-ray does not have any pre-created square rendering resolutions out-of-the-box. However, this is straightforward to fix.
- Open POV-Ray
- Go to the “tools” menu and select “edit resolution INI file”
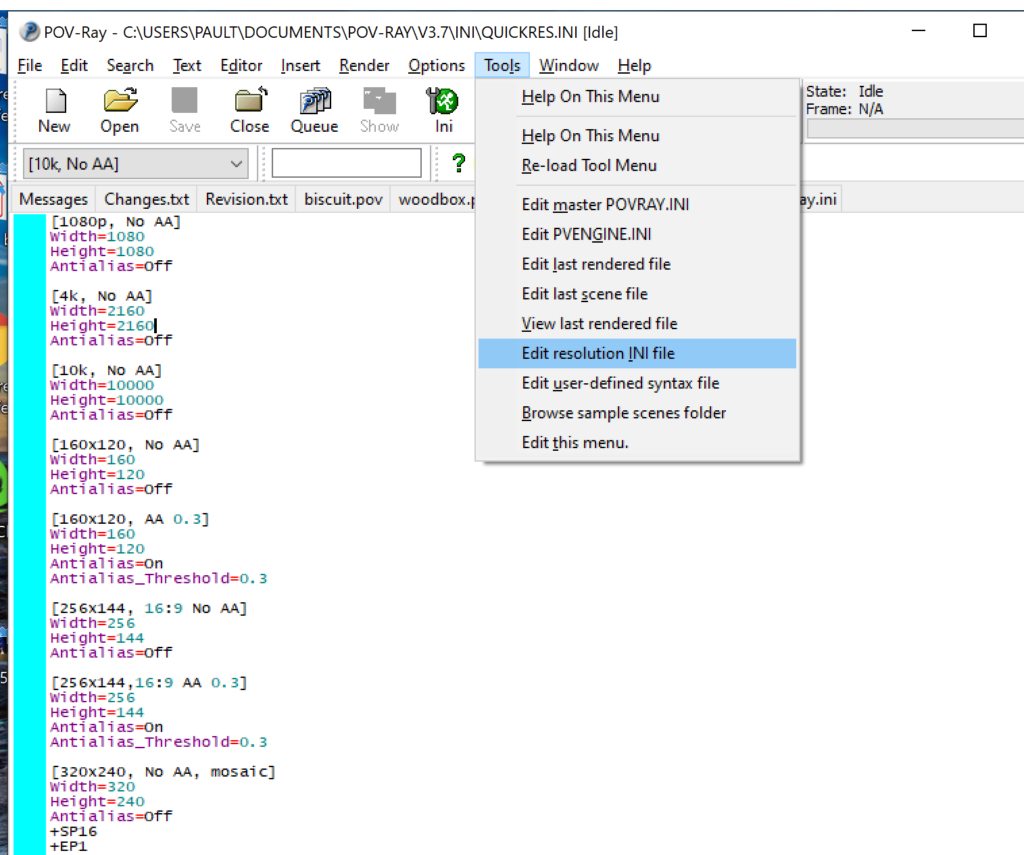
- At the top of the INI file (which opens for editing in POV-ray), make a new profile:
[1080x1080, AA] Width=480 Height=480 Antialias=On
- Make similar profiles (with unique names) to suit your preferences. I suggest one at 480×480 (as a fast preview), another at 2160×2160, and another at 5000×5000 (because they will be absurdly high resolution). For example:
[2160x2160 no AA] Width=2160 Height=2160 Antialias=Off
You can optionally make more profiles with antialiasing on (which provides some smoothing for areas of high detail), but you’re probably better off just rendering without antialiasing at higher resolutions and the scaling the image down as needed. Also, rendering without antialiasing will be faster.
- Once done making profiles, save and exit POV-Ray.
- The next time you open POV-Ray, your new resolution profiles will be available in the lefthand dropdown box.
Configuring PhysiCell-povwriter
Once you have copied povwriter-settings.xml to your project’s config file, open it in a text editor. Below, we’ll show the different settings.
Camera settings
<camera> <distance_from_origin units="micron">1500</distance_from_origin> <xy_angle>3.92699081699</xy_angle> <!-- 5*pi/4 --> <yz_angle>1.0471975512</yz_angle> <!-- pi/3 --> </camera>
For simplicity, PhysiCell-POVray (currently) always aims the camera towards the origin (0,0,0), with “up” towards the positive z-axis. distance_from_origin sets how far the camera is placed from the origin. xy_angle sets the angle \(\theta\) from the positive x-axis in the xy-plane. yz_angle sets the angle \(\phi\) from the positive z-axis in the yz-plane. Both angles are in radians.
Options
<options> <use_standard_colors>true</use_standard_colors> <nuclear_offset units="micron">0.1</nuclear_offset> <cell_bound units="micron">750</cell_bound> <threads>8</threads> </options>
use_standard_colors (if set to true) uses a built-in “paint-by-numbers” color scheme, where each cell type (identified with an integer) gets XML-defined colors for live, apoptotic, and dead cells. More on this below. If use_standard_colors is set to false, then PhysiCell-povwriter uses the my_pigment_and_finish_function in ./custom_modules/povwriter.cpp to color cells.
The nuclear_offset is a small additional height given to nuclei when cropping to avoid visual artifacts when rendering (which can cause some “tearing” or “bleeding” between the rendered nucleus and cytoplasm). cell_bound is used for leaving some cells out of bound: any cell with |x|, |y|, or |z| exceeding cell_bound will not be rendered. threads is used for parallelizing on multicore processors; note that it only speeds up povwriter if you are converting multiple PhysiCell outputs to povray files.
Save
<save> <!-- done --> <folder>output</folder> <!-- use . for root --> <filebase>output</filebase> <time_index>3696</time_index> </save>
Use folder to tell PhysiCell-povwriter where the data files are stored. Use filebase to tell how the outputs are named. Typically, they have the form output########_cells_physicell.mat; in this case, the filebase is output. Lastly, use time_index to set the output number. For example if your file is output00000182_cells_physicell.mat, then filebase = output and time_index = 182.
Below, we’ll see how to specify ranges of indices at the command line, which would supersede the time_index given here in the XML.
Clipping planes
PhysiCell-povwriter uses clipping planes to help create cutaway views of the simulations. By default, 3 clipping planes are used to cut out an octant of the viewing area.
Recall that a plane can be defined by its normal vector n and a point p on the plane. With these, the plane can be defined as all points x satisfying
\[ \left( \vec{x} -\vec{p} \right) \cdot \vec{n} = 0 \]
These are then written out as a plane equation
\[ a x + by + cz + d = 0, \]
where
\[ (a,b,c) = \vec{n} \hspace{.5in} \textrm{ and } \hspace{0.5in} d = \: – \vec{n} \cdot \vec{p}. \]
As of Version 1.0.0, we are having some difficulties with clipping planes that do not pass through the origin (0,0,0), for which \( d = 0 \).
In the config file, these planes are written as \( (a,b,c,d) \):
<clipping_planes> <!-- done --> <clipping_plane>0,-1,0,0</clipping_plane> <clipping_plane>-1,0,0,0</clipping_plane> <clipping_plane>0,0,1,0</clipping_plane> </clipping_planes>
Note that cells “behind” the plane (where \( ( \vec{x} – \vec{p} ) \cdot \vec{n} \le 0 \)) are rendered, and cells in “front” of the plane (where \( (\vec{x}-\vec{p}) \cdot \vec{n} > 0 \)) are not rendered. Cells that intersect the plane are partially rendered (using constructive geometry via union and intersection commands in POV-ray).
Cell color definitions
Within <cell_color_definitions>, you’ll find multiple <cell_colors> blocks, each of which defines the live, dead, and necrotic colors for a specific cell type (with the type ID indicated in the attribute). These colors are only applied if use_standard_colors is set to true in options. See above.
The live colors are given as two rgb (red,green,blue) colors for the cytoplasm and nucleus of live cells. Each element of this triple can range from 0 to 1, and not from 0 to 255 as in many raw image formats. Next, finish specifies ambient (how much highly-scattered background ambient light illuminates the cell), diffuse (how well light rays can illuminate the surface), and specular (how much of a shiny reflective splotch the cell gets).
See the POV-ray documentation for for information on the finish.
This is repeated to give the apoptotic and necrotic colors for the cell type.
<cell_colors type="0"> <live> <cytoplasm>.25,1,.25</cytoplasm> <!-- red,green,blue --> <nuclear>0.03,0.125</nuclear> <finish>0.05,1,0.1</finish> <!-- ambient,diffuse,specular --> </live> <apoptotic> <cytoplasm>1,0,0</cytoplasm> <!-- red,green,blue --> <nuclear>0.125,0,0</nuclear> <finish>0.05,1,0.1</finish> <!-- ambient,diffuse,specular --> </apoptotic> <necrotic> <cytoplasm>1,0.5412,0.1490</cytoplasm> <!-- red,green,blue --> <nuclear>0.125,0.06765,0.018625</nuclear> <finish>0.01,0.5,0.1</finish> <!-- ambient,diffuse,specular --> </necrotic> </cell_colors>
Use multiple cell_colors blocks (each with type corresponding to the integer cell type) to define the colors of multiple cell types.
Using PhysiCell-povwriter
Use by the XML configuration file alone
The simplest syntax:
physicell$ ./povwriter
(Windows users: povwriter or povwriter.exe) will process ./config/povwriter-settings.xml and convert the single indicated PhysiCell snapshot to a .pov file.
If you run POV-writer with the default configuration file in the povwriter structure (with the supplied sample data), it will render time index 3696 from the immunotherapy example in our 2018 PhysiCell Method Paper:
physicell$ ./povwriter povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Processing file ./output/output00003696_cells_physicell.mat... Matrix size: 32 x 66978 Creating file pov00003696.pov for output ... Writing 66978 cells ... done! Done processing all 1 files!
The result is a single POV-ray file (pov00003696.pov) in the root directory.
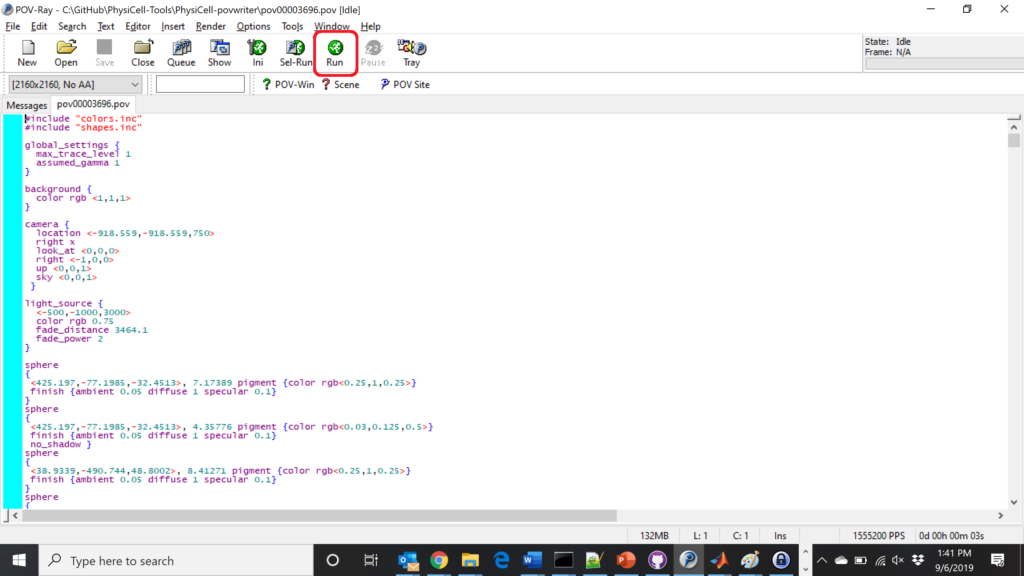
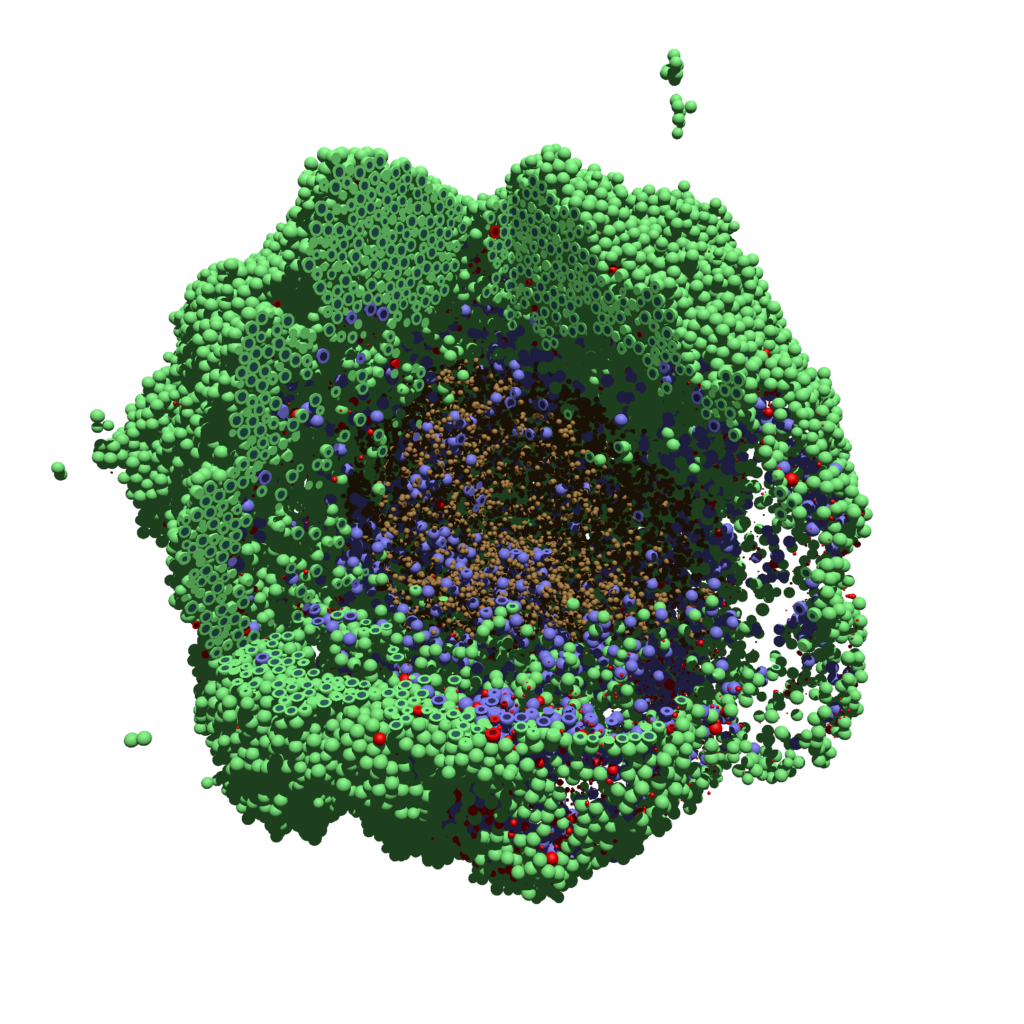
Now, open that file in POV-ray (double-click the file if you are in Windows), choose one of your resolutions in your lefthand dropdown (I’ll choose 2160×2160 no antialiasing), and click the green “run” button.
You can watch the image as it renders. The result should be a PNG file (named pov00003696.png) that looks like this:
Using command-line options to process multiple times (option #1)
Now, suppose we have more outputs to process. We still state most of the options in the XML file as above, but now we also supply a command-line argument in the form of start:interval:end. If you’re still in the povwriter project, note that we have some more sample data there. Let’s grab and process it:
physicell$ cd output physicell$ unzip more_samples.zip Archive: more_samples.zip inflating: output00000000_cells_physicell.mat inflating: output00000001_cells_physicell.mat inflating: output00000250_cells_physicell.mat inflating: output00000300_cells_physicell.mat inflating: output00000500_cells_physicell.mat inflating: output00000750_cells_physicell.mat inflating: output00001000_cells_physicell.mat inflating: output00001250_cells_physicell.mat inflating: output00001500_cells_physicell.mat inflating: output00001750_cells_physicell.mat inflating: output00002000_cells_physicell.mat inflating: output00002250_cells_physicell.mat inflating: output00002500_cells_physicell.mat inflating: output00002750_cells_physicell.mat inflating: output00003000_cells_physicell.mat inflating: output00003250_cells_physicell.mat inflating: output00003500_cells_physicell.mat inflating: output00003696_cells_physicell.mat physicell$ ls citation and license.txt more_samples.zip output00000000_cells_physicell.mat output00000001_cells_physicell.mat output00000250_cells_physicell.mat output00000300_cells_physicell.mat output00000500_cells_physicell.mat output00000750_cells_physicell.mat output00001000_cells_physicell.mat output00001250_cells_physicell.mat output00001500_cells_physicell.mat output00001750_cells_physicell.mat output00002000_cells_physicell.mat output00002250_cells_physicell.mat output00002500_cells_physicell.mat output00002750_cells_physicell.mat output00003000_cells_physicell.mat output00003250_cells_physicell.mat output00003500_cells_physicell.mat output00003696.xml output00003696_cells_physicell.mat
Let’s go back to the parent directory and run povwriter:
physicell$ ./povwriter 0:250:3500 povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Matrix size: 32 x 18317 Processing file ./output/output00000000_cells_physicell.mat... Creating file pov00000000.pov for output ... Writing 18317 cells ... Processing file ./output/output00002000_cells_physicell.mat... Matrix size: 32 x 33551 Creating file pov00002000.pov for output ... Writing 33551 cells ... Processing file ./output/output00002500_cells_physicell.mat... Matrix size: 32 x 43440 Creating file pov00002500.pov for output ... Writing 43440 cells ... Processing file ./output/output00001500_cells_physicell.mat... Matrix size: 32 x 40267 Creating file pov00001500.pov for output ... Writing 40267 cells ... Processing file ./output/output00003000_cells_physicell.mat... Matrix size: 32 x 56659 Creating file pov00003000.pov for output ... Writing 56659 cells ... Processing file ./output/output00001000_cells_physicell.mat... Matrix size: 32 x 74057 Creating file pov00001000.pov for output ... Writing 74057 cells ... Processing file ./output/output00003500_cells_physicell.mat... Matrix size: 32 x 66791 Creating file pov00003500.pov for output ... Writing 66791 cells ... Processing file ./output/output00000500_cells_physicell.mat... Matrix size: 32 x 114316 Creating file pov00000500.pov for output ... Writing 114316 cells ... done! Processing file ./output/output00000250_cells_physicell.mat... Matrix size: 32 x 75352 Creating file pov00000250.pov for output ... Writing 75352 cells ... done! Processing file ./output/output00002250_cells_physicell.mat... Matrix size: 32 x 37959 Creating file pov00002250.pov for output ... Writing 37959 cells ... done! Processing file ./output/output00001750_cells_physicell.mat... Matrix size: 32 x 32358 Creating file pov00001750.pov for output ... Writing 32358 cells ... done! Processing file ./output/output00002750_cells_physicell.mat... Matrix size: 32 x 49658 Creating file pov00002750.pov for output ... Writing 49658 cells ... done! Processing file ./output/output00003250_cells_physicell.mat... Matrix size: 32 x 63546 Creating file pov00003250.pov for output ... Writing 63546 cells ... done! done! done! done! Processing file ./output/output00001250_cells_physicell.mat... Matrix size: 32 x 54771 Creating file pov00001250.pov for output ... Writing 54771 cells ... done! done! done! done! Processing file ./output/output00000750_cells_physicell.mat... Matrix size: 32 x 97642 Creating file pov00000750.pov for output ... Writing 97642 cells ... done! done! Done processing all 15 files!
Notice that the output appears a bit out of order. This is normal: povwriter is using 8 threads to process 8 files at the same time, and sending some output to the single screen. Since this is all happening simultaneously, it’s a bit jumbled (and non-sequential). Don’t panic. You should now have created pov00000000.pov, pov00000250.pov, … , pov00003500.pov.
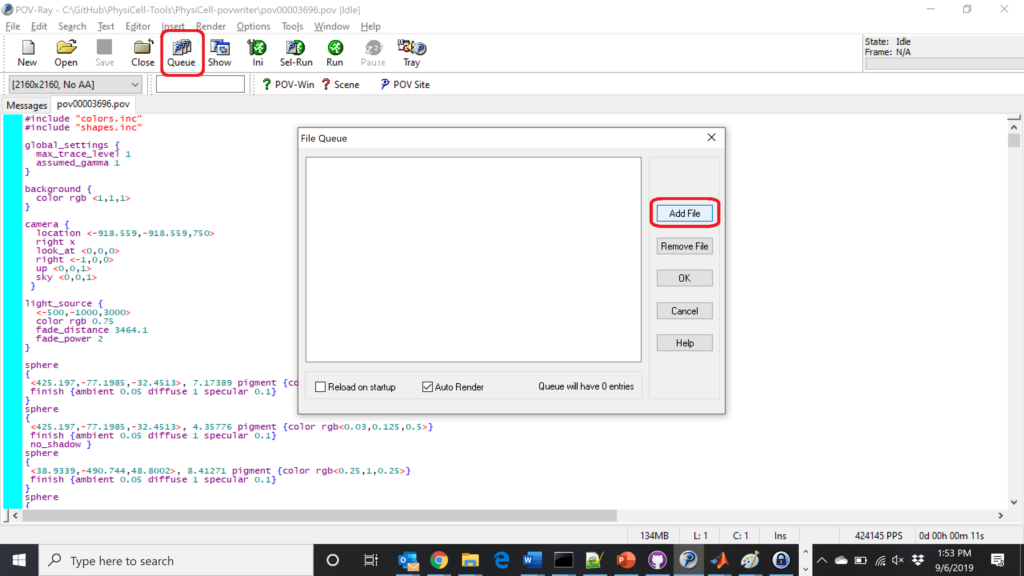
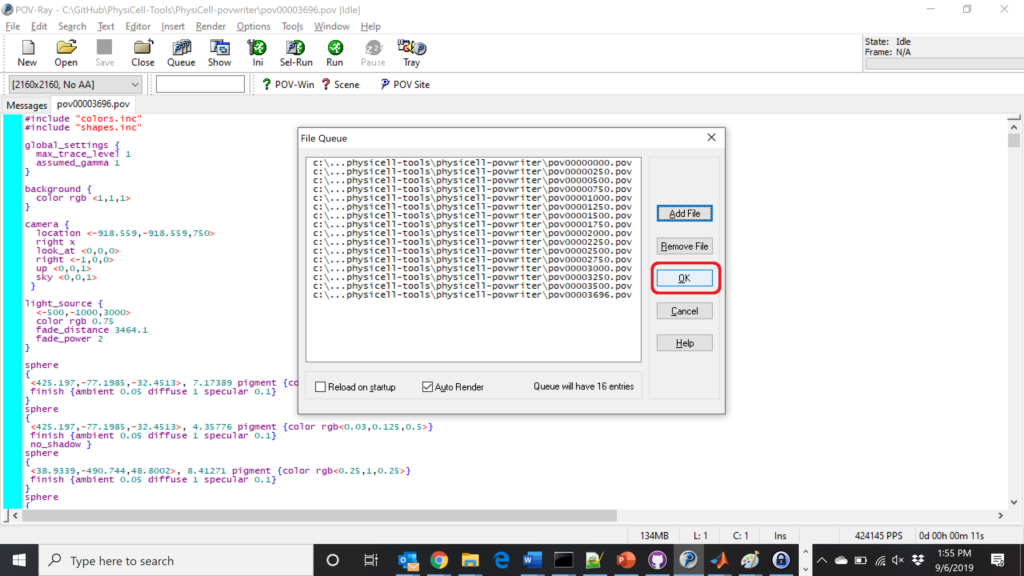
Now, go into POV-ray, and choose “queue.” Click “Add File” and select all 15 .pov files you just created:
Hit “OK” to let it render all the povray files to create PNG files (pov00000000.png, … , pov00003500.png).
Using command-line options to process multiple times (option #2)
You can also give a list of indices. Here’s how we render time indices 250, 1000, and 2250:
physicell$ ./povwriter 250,1000,2250 povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Processing file ./output/output00002250_cells_physicell.mat... Matrix size: 32 x 37959 Creating file pov00002250.pov for output ... Writing 37959 cells ... Processing file ./output/output00001000_cells_physicell.mat... Matrix size: 32 x 74057 Creating file pov00001000.pov for output ... Processing file ./output/output00000250_cells_physicell.mat... Matrix size: 32 x 75352 Writing 74057 cells ... Creating file pov00000250.pov for output ... Writing 75352 cells ... done! done! done! Done processing all 3 files!
This will create files pov00000250.pov, pov00001000.pov, and pov00002250.pov. Render them in POV-ray just as before.
Advanced options (at the source code level)
If you set use_standard_colors to false, povwriter uses the function my_pigment_and_finish_function (at the end of ./custom_modules/povwriter.cpp). Make sure that you set colors.cyto_pigment (RGB) and colors.nuclear_pigment (also RGB). The source file in povwriter has some hinting on how to write this. Note that the XML files saved by PhysiCell have a legend section that helps you do determine what is stored in each column of the matlab file.
Optional postprocessing
Image conversion / manipulation with ImageMagick
Suppose you want to convert the PNG files to JPEGs, and scale them down to 60% of original size. That’s very straightforward in ImageMagick:
physicell$ magick mogrify -format jpg -resize 60% pov*.png
Creating an animated GIF with ImageMagick
Suppose you want to create an animated GIF based on your images. I suggest first converting to JPG (see above) and then using ImageMagick again. Here, I’m adding a 20 ms delay between frames:
physicell$ magick convert -delay 20 *.jpg out.gif
Here’s the result:

Creating a compressed movie with Mencoder
Syntax coming later.
Closing thoughts and future work
In the future, we will probably allow more control over the clipping planes and a bit more debugging on how to handle planes that don’t pass through the origin. (First thoughts: we need to change how we use union and intersection commands in the POV-ray outputs.)
We should also look at adding some transparency for the cells. I’d prefer something like rgba (red-green-blue-alpha), but POV-ray uses filters and transmission, and we want to make sure to get it right.
Lastly, it would be nice to find a balance between the current very simple camera setup and better control.
Thanks for reading this PhysiCell Friday tutorial! Please do give PhysiCell at try (at http://PhysiCell.org) and read the method paper at PLoS Computational Biology.
ParaView for PhysiCell – Part 1
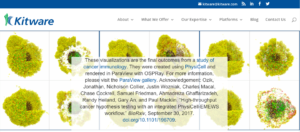
In this tutorial, we discuss the topic of visualizing data that is generated by PhysiCell. Specifically, we discuss the visualization of cells. In a later post, we’ll discuss options for visualizing the microenvironment. For 2-D models, PhysiCell generates Scalable Vector Graphics (SVG) files that depict cells’ positions, sizes (volumes), and colors (virtual pathology). Obviously, visualizing cells from 3-D models is more challenging. (Note: SVG files are also generated for 3-D models; however, they capture only the cells that intersect the Z=0 plane). Until now, we have only discussed a couple of applications for visualizing 3-D data from PhysiCell: MATLAB (or Octave) and POV-Ray. In this post, we describe ParaView: an open source, data analysis and visualization application from Kitware. ParaView can be used to visualize a wide variety of scientific data, as depicted on their gallery page.
Preliminary steps
Before we get started, just a reminder – if you have any problems or questions, please join our mailing list (physicell-users@googlegroups.com) to get help. In preparation for using the customized PhysiCell data reader in ParaView, you will need to have a specific Python module, scipy, installed. Python will be a useful language for other PhysiCell data analysis and visualization tasks too, so having it installed on your computer will come in handy later, beyond using ParaView. The confusion of installing/using Python (and the scipy module) for ParaView is due to multiple factors:
- you may or may not have Administrator permission on your computer,
- there are different versions of Python, including the major version confusion – 2 vs. 3,
- there are different distributions of Python, and
- ParaView comes with its own built-in Python (version 2), but it isn’t easily extensible.
Before we get operating system specific, we just want to point out that it is possible to have multiple versions and/or distributions of Python on your computer. Unfortunately, there is no guarantee that you can mix modules of one with another. This is especially true for one popular Python distribution, Anaconda, and any other distribution.
We now provide some detailed instructions for the primary operating systems. In the sections that follow, we assume you have Admin permission on your computer. If you do not and you need to install Python + scipy as a standard user, see Appendix A at the end.
Windows
Windows does not come with Python, by default. Therefore, you will need to download/install it from python.org – get the latest 2.x version – currently https://www.python.org/downloads/release/python-2714/.
During the installation process, you will be asked if you want to install for all users or just yourself. That is up to you.
You’ll have the option of changing the default installation directory. We recommend keeping the default: C:\Python27.
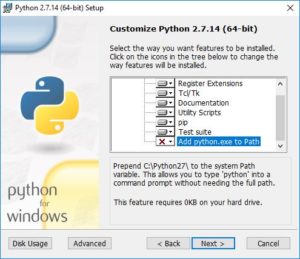
Finally, you will have the choice of having this python executable be your default. That is up to you. If you have another Python distribution installed that you want to keep as your default, then you should leave this choice unchecked, i.e. leave the “X”. But if you do want to use this one as your default, select “Add python.exe to Path”:
After completing the Python 2.7 installation, open a Command Prompt shell and run (or if you selected to use this python.exe as your default in the above step, you can just use ‘python’ instead of specifying the full path):
c:\python27\python.exe -m pip install scipy
This will download and install the scipy module which is what our PhysiCell data reader uses. You can verify that it got installed by running python and trying to import it:
c:\>python27\python.exe Python 2.7.14 (v2.7.14:84471935ed, Sep 16 2017, 20:25:58) [MSC v.1500 64 bit (AMD64)] on win32 Type "help", "copyright", "credits" or "license" for more information. >>> import scipy >>> quit()
OSX and Linux
Both OSX and Linux come with a system-level version of Python pre-installed (/usr/bin/python). Regardless of whether you have installed additional versions of Python, you will want to make sure the pre-installed version has the scipy module. OSX should already have it. However, Linux will not and you will need to install it via:
/usr/bin/python -m pip install scipy
You can test if scipy is accessible by simply trying to import it:
/usr/bin/python ... >>> import scipy >>> quit()
Installing ParaView
After you have successfully installed Python + scipy, download and install the (binary) ParaView application for your particular platform. The current, stable version is 5.4.1.
Windows
Assuming you have Admin permission, download/install ParaView-5.4.1-Qt5-OpenGL2-Windows-64bit.exe. If you do not have Admin permission, see Appendix A.
OSX or Linux
On OSX, assuming you have Admin permissions, download/install ParaView-5.4.1-Qt5-OpenGL2-MPI-OSX10.8-64bit.dmg. If you do not have Admin permission, see Appendix A.
On Linux, download ParaView-5.4.1-Qt5-OpenGL2-MPI-Linux-64bit.tar.gz and uncompress it into an appropriate directory. For example, if you want to make ParaView available to everyone, you may want to uncompress it into /usr/local. If you only want to make it available for your personal use, see Appendix A.
Running ParaView
Before starting the ParaView application, you can set an environment variable, PHYSICELL_DATA, to be the full path to the directory where the PhysiCell data can be found. This will make it easier for the custom data reader (a Python script) in the ParaView pipeline to find the data. For example, in the next section we provide a link to some sample PhysiCell data. If you simply uncompress that zip archive into your Downloads directory, then (on Linux/OSX bash) you could:
$ export PHYSICELL_DATA=/path-to-your-home-dir/Downloads
(this Windows tutorial, while aimed at editing your PATH, will also help you find the environment variables setting).
If you choose not to set the PHYSICELL_DATA environment variable, the custom data reader will look in your user Downloads directory. Alternatively, you can simply edit the ParaView custom data reader Python script to point to your data directory (and then you would probably want to File -> Save State).
NOTE: if you are using OSX and want to use the PHYSICELL_DATA environment variable, you should start the ParaView application from the Terminal, e.g. $ /Applications/ParaView-5.4.1.app/Contents/MacOS/paraview &
Finally, go ahead and start the ParaView application. You should see a blank GUI (Figure 1). Don’t be frightened by the complexity of the GUI – yes, there are several widgets, but we will walk you down a minimal path to help you visualize PhysiCell cell data. Of course you have access to all of ParaView’s documentation – the Getting Started, Guide, and Tutorial under the Help menu are a good place to start. In addition to the downloadable (.pdf) documentation, there is also in-depth information online: https://www.paraview.org/Wiki/ParaView
Figure 1. The ParaView application
Note: the 3-D axis in the lower-left corner of the RenderView does not represent the origin. It is just a reference axis to provide 3-D orientation.
Before you get started with examples, you should open ParaView’s Settings (Preferences), select the General tab, and make sure “Auto Apply” is checked. This will avoid the need to manually “Apply” changes you make to an object’s properties.
Cancer immunity 3D example
We will use sample output data from the cancer_immune_3D project – one of the sample projects bundled with PhysiCell. You can refer to the PhysiCell Quickstart guide if you want to actually compile and run that project. But to simplify this tutorial, we provide sample data (a single time step) from that project, at:
https://sourceforge.net/projects/physicell/files/Tutorials/MultiCellDS/3D_PhysiCell_matlab_sample.zip/download
After you extract the files from this .zip, the file of interest for this tutorial is called output00003696_cells_physicell.mat. (And remember, as discussed above, to set the PHYSICELL_DATA environment variable to point to the directory where you extracted the files).
Additionally, for this tutorial, you’ll need some predefined ParaView state files (*.pvsm). A state file is just what it sounds like – it saves the entire state of a ParaView session so that you can easily re-use it. For this tutorial, we have provided the following state files to help you get started:
- physicell_glyphs.pvsm – render cells as simple vertex glyphs
- physicell_z0slice.pvsm – render the intersection of spherical glyphs with the Z=0 plane
- physicell_3clip_planes_ospray.pvsm – OSPRay renderer with 3 clipping planes
- physicell_cells_animate.pvsm – demonstrate how to do animation
Download them here: physicell_paraview_states.zip
Figure 2 is the SVG image from the sample data. It depicts the (3-D) cells that intersect the Z=0 plane.

Figure 2. snapshot00003696.svg generated by PhysiCell
Reading PhysiCell (cell) data
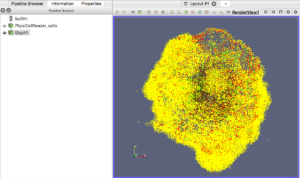
One way that ParaView offers extensibility is via Python scripts. To make it easier to read data generated by PhysiCell, we provide users with a “Programmable Source” that will read and process data in a file. In the ParaView screen-captured figures below, the Programmable Source (“PhysiCellReader_cells”) will be the very first module in the pipeline.
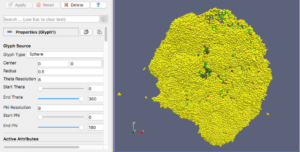
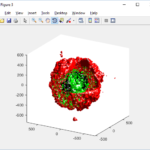
For this exercise, you can File->LoadState and select the physicell_glyphs.pvsm file that you downloaded above. Assuming you previously copied the output00003696_cells_physicell.mat sample data file into one of the default directories as described above, it should display the results in Figure 3. (Otherwise, you will likely see an error message appear, in which case see Appendix B). These are the simplest (and fastest) glyphs to represent PhysiCell cells. They are known as 2-D Vertex glyphs, although the 2-D is misleading since they are rendered in 3-space. At this point, you can interact – rotate, zoom, pan, with the visualization (rf. Sect. 4.4.2 in the ParaViewGuide-5.4.0 for an explanation of the controls, but basically: left-mouse button hold while moving cursor to rotate; Ctl-left-mouse for zoom; Ctl-Shift-left-mouse to pan).
For this particular ParaView state file, we use the following code to assign colors to cells (Note: the PhysiCell code in /custom_modules creates the SVG file using colors based on cells’ neighbor information. This information is not saved in the .mat output files, therefore we cannot faithfully reproduce SVG cell colors here):
# The following lines assign an integer to represent
# a color, defined in a Color Map.
sval = 0 # immune cells are yellow?
if val[5,idx] == 1: # [5]=cell_type
sval = 1 # lime green
if (val[6,idx] == 6) or (val[6,idx] == 7):
sval = 0
if val[7,idx] == 100: # [7]=current_phase
sval = 3 # apoptotic: red
if val[7,idx] > 100 and val[7,idx] < 104:
sval = 2 # necrotic: brownish
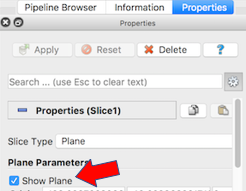
The next exercise is a simple extension of the previous. We want to add a slice to our pipeline that will intersect the cells (spherical glyphs). Assuming the slice is the Z=0 plane, this will approximate the SVG in Figure 2. So, select Edit->ResetSession to start from scratch, then File->LoadState and select the physicell_z0slice.pvsm file. Note that the “Glyph1” node in the pipeline is invisible (its “eyeball” is toggled off). If you make it visible (select the eyeball), you will essentially reproduce Figure 4. But for this exercise, we want Glyph1 to be invisible and Slice1 visible. If you select Slice1 (its green box) in the pipeline, you can select its Properties tab (at the top) to see all its properties. Of particular interest is the “Show Plane” checkbox at the top.
If this is checked on, you can interactively translate the plane along its normal, as well as select and rotate the normal itself. Try it! You can also “hardcode” the slice plane parameters in its properties panel.
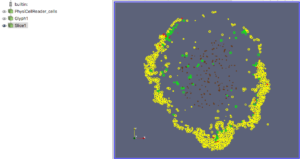
Figure 5. Z=0 slice through the spherical glyphs (approximate SVG slice)
Our final exercise with the sample dataset is to visualize cells using a higher quality renderer in ParaView known as OSPRay. So, as before, Edit->ResetSession to start from scratch, then File->LoadState and select the physicell_3clip_planes_ospray.pvsm file. This will create a pipeline that has 3 clipping planes aligned such that an octant of our spheroidal cell cluster is clipped away, letting us peer into its core (Figure 6). As with the previous slice plane, you can interactively reposition one or more of the clipping planes here.
Note: One (temporary) downside of using the OSPRay renderer is that cells (spheres) cannot be arbitrarily scaled in size. This will be fixed in a future release of ParaView. For now, we get around that by shrinking the distance of each cell from the origin. Obviously this is not a perfect solution, but for cells that are sort of clustered around the origin, it offers a decent approximation. We mention this 1) to disclose the inaccuracy, and 2) in case you look at the data ranges in the “Information” view/tab and notice they are not reflecting the domain of your simulation.
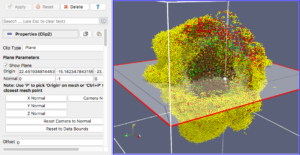
Figure 6. OSPRay-rendered cells, showing 1 of 3 interactive clipping planes
Animation in Time
At some point, you’ll want to see the dynamics of your simulation. This is where ParaView’s animation functionality comes in handy. It provides an easy way to let you render all (or a subset) of your PhysiCell output files, control the animation, and also save images (as .png files).
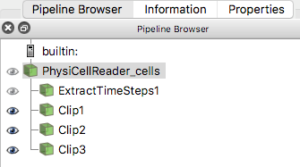
For this exercise, you will obviously want to have generated multiple output files from a PhysiCell project. Once you have those, e.g. from the cancer_immune_3D project, you can File->LoadState and select the physicell_cells_animate.pvsm file. This will show the following pipeline:
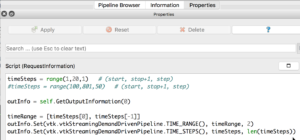
If you select the PhysiCellReader_cells (green box; leave its “eye” icon deselected) and click on the Properties tab, you will have access to the Script(RequestInformation) (you may need to click the “gear” icon next to the Properties tab Search bar to “Toggle advanced properties” to see this script):
In there, you will see the lines:
timeSteps = range(1,20,1) # (start, stop+1, step) #timeSteps = range(100,801,50) # (start, stop+1 [, step])
You’ll want to edit the first line, specifying your desired start, stop, and (optionally) step values for your files’ numeric suffixes. We happened to use the second timeSteps line (currently commented out with the ‘#’) for data from our simulation, which resulted in 15 time steps (0-14) for the time values: 100,150,200,…800. Pressing the Play (center) button of the animation icons would animate those frames:
When you like what you see, you can select File->SaveAnimation to save the images. After you provide some minimal information for those images, e.g., resolution and filename prefix, press “OK” and you will see a horizontal progress bar being updated below the render window. After the animation images are generated, you can use your favorite image processing and movie generation tools to post-process them. In Figure 7, we used ImageMagick’s montage command to arrange the 15 images from a cancer_immune_3D simulation. And for generating a movie file, take a look at mplayer/mencoder as one open source option.
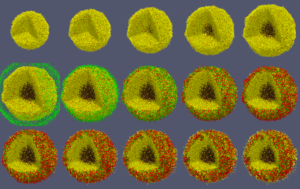
Figure 7. Images from cancer_immune_3D
Further Help
For questions specific to PhysiCell, have a look at our User Guide and join our mailing list to ask questions. For ParaView, have a look at their User Guide and join the ParaView mailing list to ask questions.
Thanks!
In closing, we would like to thank Kitware for their terrific open source software and the ParaView community (especially David DeMarle and Utkarsh Ayachit) for being so helpful answering questions and providing insight. We were honored that some of our early results got headlined on Kitware’s home page!
Appendix A: Installing without Admin permission
If you do not have Admin permission on your computer, we provide instructions for installing Python + scipy and ParaView using alternative approaches.
Windows
To install Python on Windows, without Admin permission, run the msiexec command on the .msi Python installer that you downloaded, specifying a (non-system) directory in which it should be installed via the targetdir keyword. After that completes, Python will be installed; however, the python command will not be in your PATH, i.e., it will not be globally accessible.
C:\Users\sue\Downloads>msiexec /a python-2.7.14.amd64.msi /qb targetdir=c:\py27 C:\Users\sue\Downloads>python 'python' is not recognized as an internal or external command, operable program or batch file. C:\Users\sue\Downloads>cd c:\py27 c:\py27>.\python.exe Python 2.7.14 (v2.7.14:84471935ed, Sep 16 2017, 20:25:58) [MSC v.1500 64 bit (AMD64)] on win32 Type "help", "copyright", "credits" or "license" for more information. >>>
Finally, download ParaView-5.4.1-Qt5-OpenGL2-Windows-64bit.zip and extract its contents into a permissible directory, e.g. under your home folder: C:\Users\sue\ParaView-5.4.1-Qt5-OpenGL2-Windows-64bit\
Then, in ParaView, using the Tools menu, open the Python Shell, and see if you can import scipy via:
>>> sys.path.insert(0,'c:\py27\Lib\site-packages') >>> import scipy
Before proceeding with the tutorial using the PhysiCell state files, you will want to open ParaView’s Settings and check (toggle on) the “Auto Apply” property in the General settings tab.
OSX
OSX comes with a system Python pre-installed. And, at least with fairly recent versions of OSX, it comes with the scipy module also. You can test to see if that is the case on your system:
/usr/bin/python >>> import scipy
To install ParaView, download a .pkg, not a .dmg, e.g. ParaView-5.4.1-Qt5-OpenGL2-MPI-OSX10.8-64bit.pkg. Then expand that .pkg contents into a permissible directory and untar its “Payload” which contains the actual paraview executable that you can open/run:
cd ~/Downloads pkgutil --expand ParaView-5.4.1-Qt5-OpenGL2-MPI-OSX10.8-64bit.pkg ~/paraview cd ~/paraview tar -xvf Payload open Contents/MacOS/paraview
Linux
Like OSX, Linux also comes with a system Python pre-installed. However, it does not come with the scipy module. To install the scipy Python module, run:
/usr/bin/python -m pip install scipy --user
To install and run ParaView, download the .tar.gz file, e.g. ParaView-5.4.1-Qt5-OpenGL2-MPI-Linux-64bit.tar.gz and uncompress it into a permissible directory. For example, from your home directory (after downloading):
mv ~/Downloads/ParaView-5.4.1-Qt5-OpenGL2-MPI-Linux-64bit.tar.gz . tar -xvzf ParaView-5.4.1-Qt5-OpenGL2-MPI-Linux-64bit.tar.gz cd ParaView-5.4.1-Qt5-OpenGL2-MPI-Linux-64bit/bin ./paraview
Appendix B: Editing the PhysiCellReader_cells Python Script
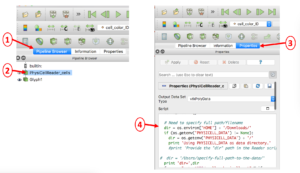
In case you encounter an error reading your .mat file(s) containing cell data, you will probably need to manually edit the directory path to the file. This is illustrated below in a 4-step process: 1) select the Pipeline Browser tab, 2) select the PhysiCellReader_cells object, 3) select its Properties, then 4) edit the relevant information in the (Python) script. (The script frame is scrollable).
Working with PhysiCell MultiCellDS digital snapshots in Matlab
PhysiCell 1.2.1 and later saves data as a specialized MultiCellDS digital snapshot, which includes chemical substrate fields, mesh information, and a readout of the cells and their phenotypes at single simulation time point. This tutorial will help you learn to use the matlab processing files included with PhysiCell.
This tutorial assumes you know (1) how to work at the shell / command line of your operating system, and (2) basic plotting and other functions in Matlab.
Key elements of a PhysiCell digital snapshot
A PhysiCell digital snapshot (a customized form of the MultiCellDS digital simulation snapshot) includes the following elements saved as XML and MAT files:
- output12345678.xml : This is the “base” output file, in MultiCellDS format. It includes key metadata such as when the file was created, the software, microenvironment information, and custom data saved at the simulation time. The Matlab files read this base file to find other related files (listed next). Example: output00003696.xml
- initial_mesh0.mat : This is the computational mesh information for BioFVM at time 0.0. Because BioFVM and PhysiCell do not use moving meshes, we do not save this data at any subsequent time.
- output12345678_microenvironment0.mat : This saves each biochemical substrate in the microenvironment at the computational voxels defined in the mesh (see above). Example: output00003696_microenvironment0.mat
- output12345678_cells.mat : This saves very basic cellular information related to BioFVM, including cell positions, volumes, secretion rates, uptake rates, and secretion saturation densities. Example: output00003696_cells.mat
- output12345678_cells_physicell.mat : This saves extra PhysiCell data for each cell agent, including volume information, cell cycle status, motility information, cell death information, basic mechanics, and any user-defined custom data. Example: output00003696_cells_physicell.mat
These snapshots make extensive use of Matlab Level 4 .mat files, for fast, compact, and well-supported saving of array data. Note that even if you cannot ready MultiCellDS XML files, you can work to parse the .mat files themselves.
The PhysiCell Matlab .m files
Every PhysiCell distribution includes some matlab functions to work with PhysiCell digital simulation snapshots, stored in the matlab subdirectory. The main ones are:
- composite_cutaway_plot.m : provides a quick, coarse 3-D cutaway plot of the discrete cells, with different colors for live (red), apoptotic (b), and necrotic (black) cells.
- read_MultiCellDS_xml.m : reads the “base” PhysiCell snapshot and its associated matlab files.
- set_MCDS_constants.m : creates a data structure MCDS_constants that has the same constants as PhysiCell_constants.h. This is useful for identifying cell cycle phases, etc.
- simple_cutaway_plot.m : provides a quick, coarse 3-D cutaway plot of user-specified cells.
- simple_plot.m : provides, a quick, coarse 3-D plot of the user-specified cells, without a cutaway or cross-sectional clipping plane.
A note on GNU Octave
Unfortunately, GNU octave does not include XML file parsing without some significant user tinkering. And one you’re done, it is approximately one order of magnitude slower than Matlab. Octave users can directly import the .mat files described above, but without the helpful metadata in the XML file. We’ll provide more information on the structure of these MAT files in a future blog post. Moreover, we plan to provide python and other tools for users without access to Matlab.
A sample digital snapshot
We provide a 3-D simulation snapshot from the final simulation time of the cancer-immune example in Ghaffarizadeh et al. (2017, in review) at:
The corresponding SVG cross-section for that time (through z = 0 μm) looks like this:
Unzip the sample dataset in any directory, and make sure the matlab files above are in the same directory (or in your Matlab path). If you’re inside matlab:
!unzip 3D_PhysiCell_matlab_sample.zip
Loading a PhysiCell MultiCellDS digital snapshot
Now, load the snapshot:
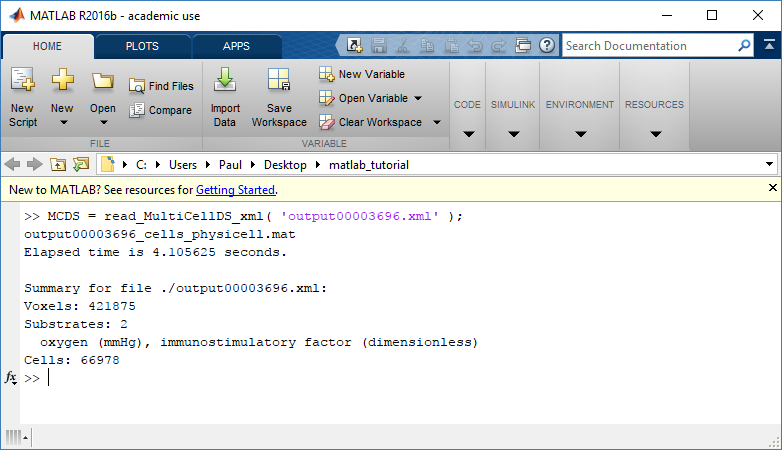
MCDS = read_MultiCellDS_xml( 'output00003696.xml');
This will load the mesh, substrates, and discrete cells into the MCDS data structure, and give a basic summary:
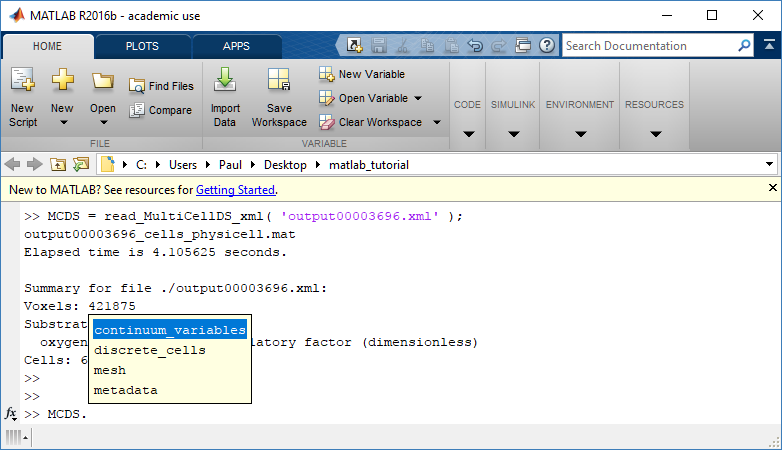
Typing ‘MCDS’ and then hitting ‘tab’ (for auto-completion) shows the overall structure of MCDS, stored as metadata, mesh, continuum variables, and discrete cells:
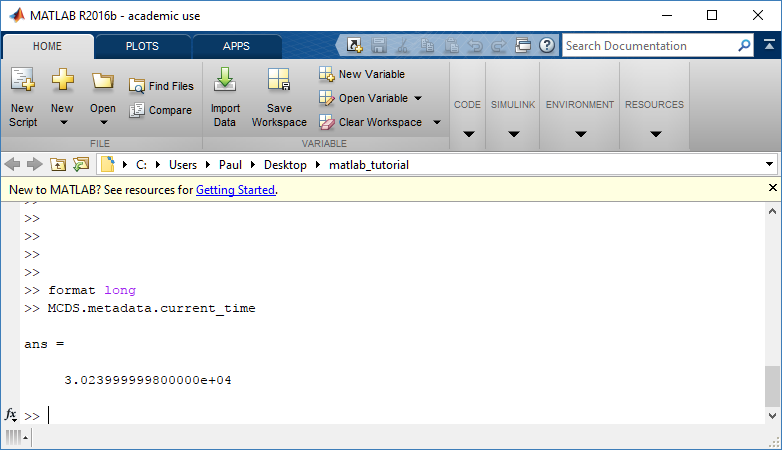
To get simulation metadata, such as the current simulation time, look at MCDS.metadata.current_time
Here, we see that the current simulation time is 30240 minutes, or 21 days. MCDS.metadata.current_runtime gives the elapsed walltime to up to this point: about 53 hours (1.9e5 seconds), including file I/O time to write full simulation data once per 3 simulated minutes after the start of the adaptive immune response.
Plotting chemical substrates
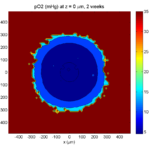
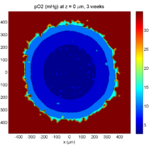
Let’s make an oxygen contour plot through z = 0 μm. First, we find the index corresponding to this z-value:
k = find( MCDS.mesh.Z_coordinates == 0 );
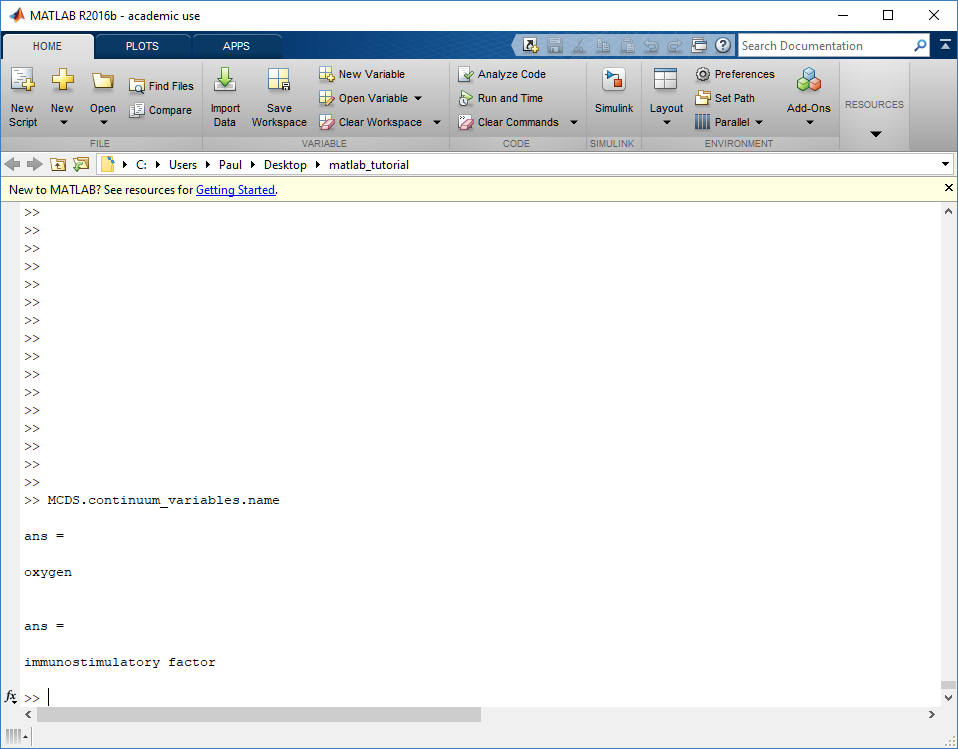
Next, let’s figure out which variable is oxygen. Type “MCDS.continuum_variables.name”, which will show the array of variable names:
Here, oxygen is the first variable, (index 1). So, to make a filled contour plot:
contourf( MCDS.mesh.X(:,:,k), MCDS.mesh.Y(:,:,k), ...
MCDS.continuum_variables(1).data(:,:,k) , 20 ) ;
Now, let’s set this to a correct aspect ratio (no stretching in x or y), add a colorbar, and set the axis labels, using
metadata to get labels:
axis image colorbar xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) ); ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
Lastly, let’s add an appropriate (time-based) title:
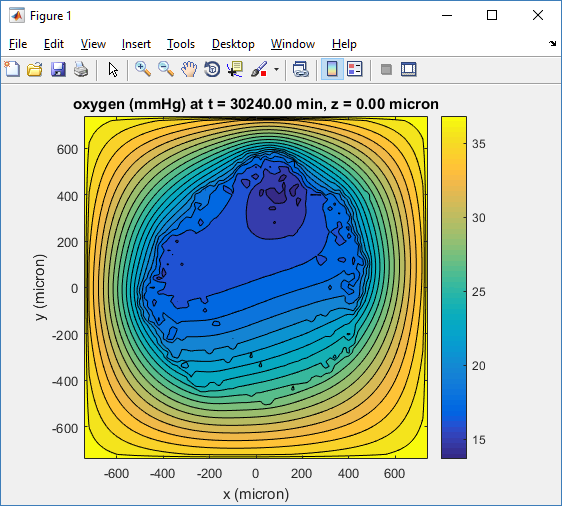
title( sprintf('%s (%s) at t = %3.2f %s, z = %3.2f %s', MCDS.continuum_variables(1).name , ...
MCDS.continuum_variables(1).units , ...
MCDS.metadata.current_time , ...
MCDS.metadata.time_units, ...
MCDS.mesh.Z_coordinates(k), ...
MCDS.metadata.spatial_units ) );
Here’s the end result:
We can easily export graphics, such as to PNG format:
print( '-dpng' , 'output_o2.png' );
For more on plotting BioFVM data, see the tutorial
at http://www.mathcancer.org/blog/saving-multicellds-data-from-biofvm/
Plotting cells in space
3-D point cloud
First, let’s plot all the cells in 3D:
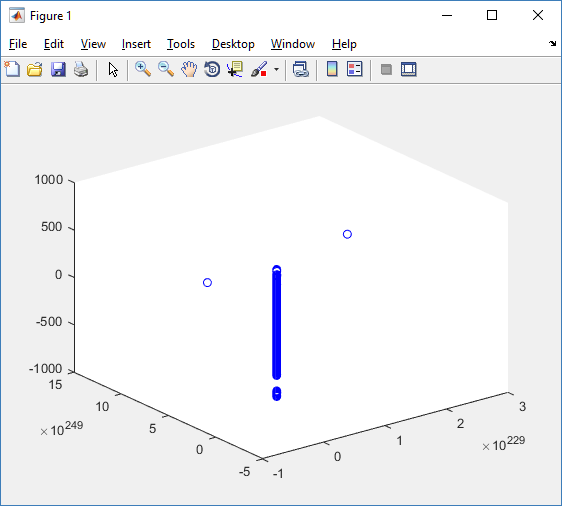
plot3( MCDS.discrete_cells.state.position(:,1) , MCDS.discrete_cells.state.position(:,2), ... MCDS.discrete_cells.state.position(:,3) , 'bo' );
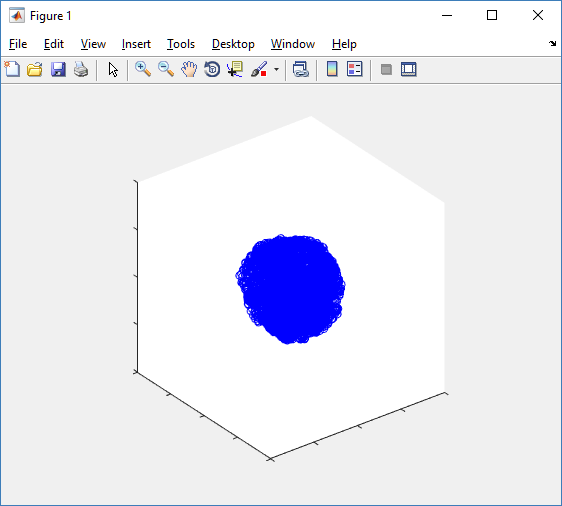
At first glance, this does not look good: some cells are far out of the simulation domain, distorting the automatic range of the plot:
This does not ordinarily happen in PhysiCell (the default cell mechanics functions have checks to prevent such behavior), but this example includes a simple Hookean elastic adhesion model for immune cell attachment to tumor cells. In rare circumstances, an attached tumor cell or immune cell can apoptose on its own (due to its background apoptosis rate),
without “knowing” to detach itself from the surviving cell in the pair. The remaining cell attempts to calculate its elastic velocity based upon an invalid cell position (no longer in memory), creating an artificially large velocity that “flings” it out of the simulation domain. Such cells are not simulated any further, so this is effectively equivalent to an extra apoptosis event (only 3 cells are out of the simulation domain after tens of millions of cell-cell elastic adhesion calculations). Future versions of this example will include extra checks to prevent this rare behavior.
The plot can simply be fixed by changing the axis:
axis( 1000*[-1 1 -1 1 -1 1] ) axis square
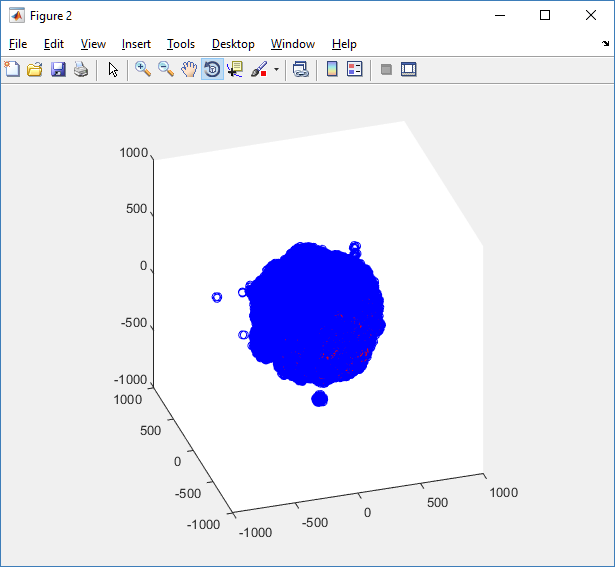
Notice that this is a very difficult plot to read, and very non-interactive (laggy) to rotation and scaling operations. We can make a slightly nicer plot by searching for different cell types and plotting them with different colors:
% make it easier to work with the cell positions;
P = MCDS.discrete_cells.state.position;
% find type 1 cells
ind1 = find( MCDS.discrete_cells.metadata.type == 1 );
% better still, eliminate those out of the simulation domain
ind1 = find( MCDS.discrete_cells.metadata.type == 1 & ...
abs(P(:,1))' < 1000 & abs(P(:,2))' < 1000 & abs(P(:,3))' < 1000 );
% find type 0 cells
ind0 = find( MCDS.discrete_cells.metadata.type == 0 & ...
abs(P(:,1))' < 1000 & abs(P(:,2))' < 1000 & abs(P(:,3))' < 1000 );
%now plot them
P = MCDS.discrete_cells.state.position;
plot3( P(ind0,1), P(ind0,2), P(ind0,3), 'bo' )
hold on
plot3( P(ind1,1), P(ind1,2), P(ind1,3), 'ro' )
hold off
axis( 1000*[-1 1 -1 1 -1 1] )
axis square
However, this isn’t much better. You can use the scatter3 function to gain more control on the size and color of the plotted cells, or even make macros to plot spheres in the cell locations (with shading and lighting), but Matlab is very slow when plotting beyond 103 cells. Instead, we recommend the faster preview functions below for data exploration, and higher-quality plotting (e.g., by POV-ray) for final publication-
Fast 3-D cell data previewers
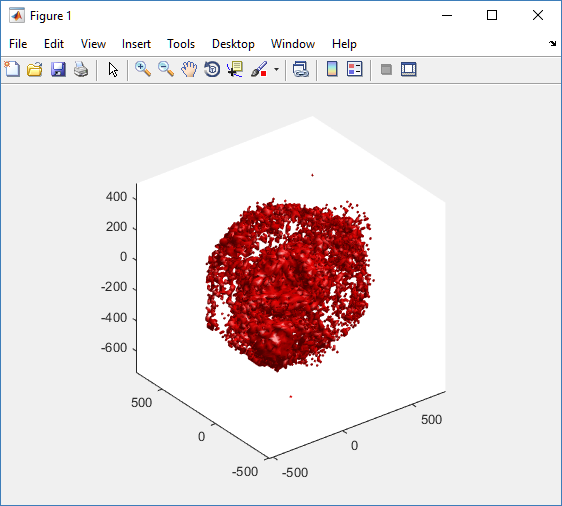
Notice that plot3 and scatter3 are painfully slow for any nontrivial number of cells. We can use a few fast previewers to quickly get a sense of the data. First, let’s plot all the dead cells, and make them red:
clf simple_plot( MCDS, MCDS, MCDS.discrete_cells.dead_cells , 'r' )
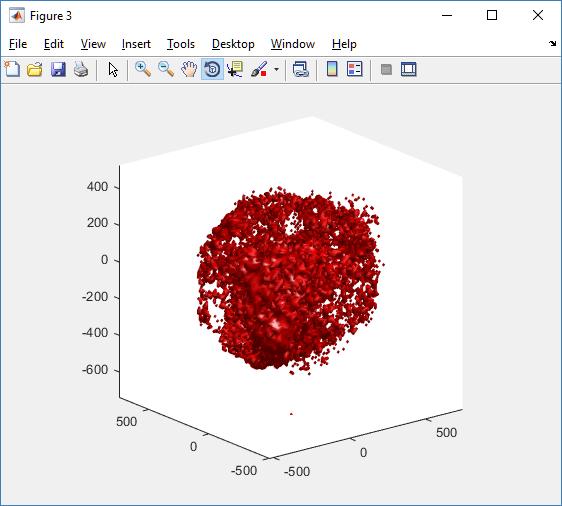
This function creates a coarse-grained 3-D indicator function (0 if no cells are present; 1 if they are), and plots a 3-D level surface. It is very responsive to rotations and other operations to explore the data. You may notice the second argument is a list of indices: only these cells are plotted. This gives you a method to select cells with specific characteristics when plotting. (More on that below.) If you want to get a sense of the interior structure, use a cutaway plot:
clf simple_cutaway_plot( MCDS, MCDS, MCDS.discrete_cells.dead_cells , 'r' )
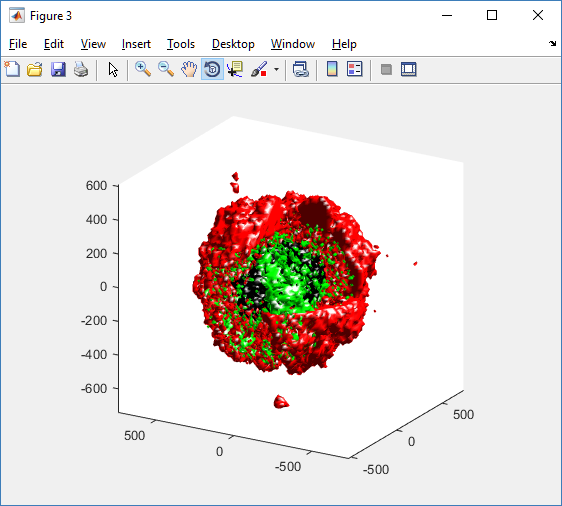
We also provide a fast “composite” cutaway which plots all live cells as red, apoptotic cells as blue (without the cutaway), and all necrotic cells as black:
clf composite_cutaway_plot( MCDS )

Lastly, we show an improved plot that uses different colors for the immune cells, and Matlab’s “find” function to help set up the indexing:
constants = set_MCDS_constants
% find the type 0 necrotic cells
ind0_necrotic = find( MCDS.discrete_cells.metadata.type == 0 & ...
(MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic_swelling | ...
MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic_lysed | ...
MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic) );
% find the live type 0 cells
ind0_live = find( MCDS.discrete_cells.metadata.type == 0 & ...
(MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic_swelling & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic_lysed & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.apoptotic) );
clf
% plot live tumor cells red, in cutaway view
simple_cutaway_plot( MCDS, ind0_live , 'r' );
hold on
% plot dead tumor cells black, in cutaway view
simple_cutaway_plot( MCDS, ind0_necrotic , 'k' )
% plot all immune cells, but without cutaway (to show how they infiltrate)
simple_plot( MCDS, ind1, 'g' )
hold off
A small cautionary note on future compatibility
PhysiCell 1.2.1 uses the <custom> data tag (allowed as part of the MultiCellDS specification) to encode its cell data, to allow a more compact data representation, because the current PhysiCell daft does not support such a formulation, and Matlab is painfully slow at parsing XML files larger than ~50 MB. Thus, PhysiCell snapshots are not yet fully compatible with general MultiCellDS tools, which would by default ignore custom data. In the future, we will make available converter utilities to transform “native” custom PhysiCell snapshots to MultiCellDS snapshots that encode all the cellular information in a more verbose but compatible XML format.
Closing words and future work
Because Octave is not a great option for parsing XML files (with critical MultiCellDS metadata), we plan to write similar functions to read and plot PhysiCell snapshots in Python, as an open source alternative. Moreover, our lab in the next year will focus on creating further MultiCellDS configuration, analysis, and visualization routines. We also plan to provide additional 3-D functions for plotting the discrete cells and varying color with their properties.
In the longer term, we will develop open source, stand-alone analysis and visualization tools for MultiCellDS snapshots (including PhysiCell snapshots). Please stay tuned!
Building a Cellular Automaton Model Using BioFVM
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM. See below for guides to setting up a C++ compiler in Windows or OSX.
What you’ll need
- A working C++ development environment with support for OpenMP. See these prior tutorials if you need help.
- A download of BioFVM, available at http://BioFVM.MathCancer.org and http://BioFVM.sf.net. Use Version 1.1.4 or later.
- The source code for this project (see below).
Matlab or Octave for visualization. Matlab might be available for free at your university. Octave is open source and available from a variety of sources.
Our modeling task
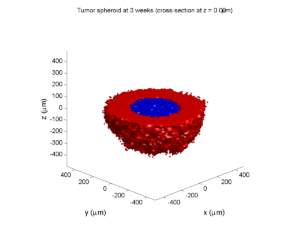
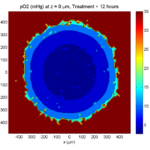
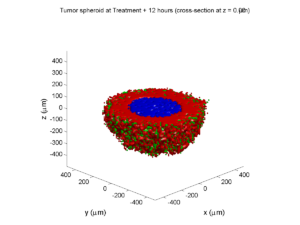
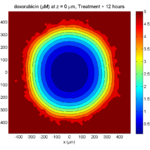
We will implement a basic 3-D cellular automaton model of tumor growth in a well-mixed fluid, containing oxygen pO2 (mmHg) and a drug c (e.g., doxorubicin, μM), inspired by modeling by Alexander Anderson, Heiko Enderling, Jan Poleszczuk, Gibin Powathil, and others. (I highly suggest seeking out the sophisticated cellular automaton models at Moffitt’s Integrated Mathematical Oncology program!) This example shows you how to extend BioFVM into a new cellular automaton model. I’ll write a similar post on how to add BioFVM into an existing cellular automaton model, which you may already have available.
Tumor growth will be driven by oxygen availability. Tumor cells can be live, apoptotic (going through energy-dependent cell death, or necrotic (undergoing death from energy collapse). Drug exposure can both trigger apoptosis and inhibit cell cycling. We will model this as growth into a well-mixed fluid, with pO2 = 38 mmHg (about 5% oxygen: a physioxic value) and c = 5 μM.
Mathematical model
As a cellular automaton model, we will divide 3-D space into a regular lattice of voxels, with length, width, and height of 15 μm. (A typical breast cancer cell has radius around 9-10 μm, giving a typical volume around 3.6×103 μm3. If we make each lattice site have the volume of one cell, this gives an edge length around 15 μm.)
In voxels unoccupied by cells, we approximate a well-mixed fluid with Dirichlet nodes, setting pO2 = 38 mmHg, and initially setting c = 0. Whenever a cell dies, we replace it with an empty automaton, with no Dirichlet node. Oxygen and drug follow the typical diffusion-reaction equations:
\[ \frac{ \partial \textrm{pO}_2 }{\partial t} = D_\textrm{oxy} \nabla^2 \textrm{pO}_2 – \lambda_\textrm{oxy} \textrm{pO}_2 – \sum_{ \textrm{cells} i} U_{i,\textrm{oxy}} \textrm{pO}_2 \]
\[ \frac{ \partial c}{ \partial t } = D_c \nabla^2 c – \lambda_c c – \sum_{\textrm{cells }i} U_{i,c} c \]
where each uptake rate is applied across the cell’s volume. We start the treatment by setting c = 5 μM on all Dirichlet nodes at t = 504 hours (21 days). For simplicity, we do not model drug degradation (pharmacokinetics), to approximate the in vitro conditions.
In any time interval [t,t+Δt], each live tumor cell i has a probability pi,D of attempting division, probability pi,A of apoptotic death, and probability pi,N of necrotic death. (For simplicity, we ignore motility in this version.) We relate these to the birth rate bi, apoptotic death rate di,A, and necrotic death rate di,N by the linearized equations (from Macklin et al. 2012):
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes apoptotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,A}(t) \Delta t\Bigr) \approx d_{i,A}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ attempts division in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -b_i(t) \Delta t\Bigr) \approx b_{i}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes necrotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,N}(t) \Delta t\Bigr) \approx d_{i,N}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{dead cell } i \textrm{ lyses in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -\frac{1}{T_{i,D}} \Delta t\Bigr) \approx \frac{ \Delta t}{T_{i,D}} \]
(Illustrative) parameter values
We use Doxy = 105 μm2/min (Ghaffarizadeh et al. 2016), and we set Ui,oxy = 20 min-1 (to give an oxygen diffusion length scale of about 70 μm, with steeper gradients than our typical 100 μm length scale). We set λoxy = 0.01 min-1 for a 1 mm diffusion length scale in fluid.
We set Dc = 300 μm2/min, and Uc = 7.2×10-3 min-1 (Dc from Weinberg et al. (2007), and Ui,c twice as large as the reference value in Weinberg et al. (2007) to get a smaller diffusion length scale of about 204 μm). We set λc = 3.6×10-5 min-1 to give a drug diffusion length scale of about 2.9 mm in fluid.
We use TD = 8.6 hours for apoptotic cells, and TD = 60 days for necrotic cells (Macklin et al., 2013). However, note that necrotic and apoptotic cells lose volume quickly, so one may want to revise those time scales to match the point where a cell loses 90% of its volume.
Functional forms for the birth and death rates
We model pharmacodynamics with an area-under-the-curve (AUC) type formulation. If c(t) is the drug concentration at any cell i‘s location at time t, then let its integrated exposure Ei(t) be
\[ E_i(t) = \int_0^t c(s) \: ds \]
and we model its response with a Hill function
\[ R_i(t) = \frac{ E_i^h(t) }{ \alpha_i^h + E_i^h(t) }, \]
where h is the drug’s Hill exponent for the cell line, and α is the exposure for a half-maximum effect.
We model the microenvironment-dependent birth rate by:
\[ b_i(t) = \left\{ \begin{array}{lr} b_{i,P} \left( 1 – \eta_i R_i(t) \right) & \textrm{ if } \textrm{pO}_{2,P} < \textrm{pO}_2 \\ \\ b_{i,P} \left( \frac{\textrm{pO}_{2}-\textrm{pO}_{2,N}}{\textrm{pO}_{2,P}-\textrm{pO}_{2,N}}\right) \Bigl( 1 – \eta_i R_i(t) \Bigr) & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_2 \le \textrm{pO}_{2,P} \\ \\ 0 & \textrm{ if } \textrm{pO}_2 \le \textrm{pO}_{2,N}\end{array} \right. \]
where pO2,P is the physioxic oxygen value (38 mmHg), and pO2,N is a necrotic threshold (we use 5 mmHg), and 0 < η < 1 the drug’s birth inhibition. (A fully cytostatic drug has η = 1.)
We model the microenvironment-dependent apoptosis rate by:
\[ d_{i,A}(t) = d_{i,A}^* + \Bigl( d_{i,A}^\textrm{max} – d_{i,A}^* \Bigr) R_i(t) \]
\[ d_{i,N}(t) = \left\{ \begin{array}{lr} 0 & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_{2} \\ \\ d_{i,N}^* & \textrm{ if } \textrm{pO}_{2} \le \textrm{pO}_{2,N} \end{array}\right. \]
(Illustrative) parameter values
We use bi,P = 0.05 hour-1 (for a 20 hour cell cycle in physioxic conditions), di,A* = 0.01 bi,P, and di,N* = 0.04 hour-1 (so necrotic cells survive around 25 hours in low oxygen conditions).
We set α = 30 μM*hour (so that cells reach half max response after 6 hours’ exposure at a maximum concentration c = 5 μM), h = 2 (for a smooth effect), η = 0.25 (so that the drug is partly cytostatic), and di,Amax = 0.1 hour^-1 (so that cells survive about 10 hours after reaching maximum response).
Building the Cellular Automaton Model in BioFVM
BioFVM already includes Basic_Agents for cell-based substrate sources and sinks. We can extend these basic agents into full-fledged automata, and then arrange them in a lattice to create a full cellular automata model. Let’s sketch that out now.
Extending Basic_Agents to Automata
The main idea here is to define an Automaton class which extends (and therefore includes) the Basic_Agent class. This will give each Automaton full access to the microenvironment defined in BioFVM, including the ability to secrete and uptake substrates. We also make sure each Automaton “knows” which microenvironment it lives in (contains a pointer pMicroenvironment), and “knows” where it lives in the cellular automaton lattice. (More on that in the following paragraphs.)
So, as a schematic (just sketching out the most important members of the class):
class Standard_Data; // define per-cell biological data, such as phenotype,
// cell cycle status, etc..
class Custom_Data; // user-defined custom data, specific to a model.
class Automaton : public Basic_Agent
{
private:
Microenvironment* pMicroenvironment;
CA_Mesh* pCA_mesh;
int voxel_index;
protected:
public:
// neighbor connectivity information
std::vector<Automaton*> neighbors;
std::vector<double> neighbor_weights;
Standard_Data standard_data;
void (*current_state_rule)( Automaton& A , double );
Automaton();
void copy_parameters( Standard_Data& SD );
void overwrite_from_automaton( Automaton& A );
void set_cellular_automaton_mesh( CA_Mesh* pMesh );
CA_Mesh* get_cellular_automaton_mesh( void ) const;
void set_voxel_index( int );
int get_voxel_index( void ) const;
void set_microenvironment( Microenvironment* pME );
Microenvironment* get_microenvironment( void );
// standard state changes
bool attempt_division( void );
void become_apoptotic( void );
void become_necrotic( void );
void perform_lysis( void );
// things the user needs to define
Custom_Data custom_data;
// use this rule to add custom logic
void (*custom_rule)( Automaton& A , double);
};
So, the Automaton class includes everything in the Basic_Agent class, some Standard_Data (things like the cell state and phenotype, and per-cell settings), (user-defined) Custom_Data, basic cell behaviors like attempting division into an empty neighbor lattice site, and user-defined custom logic that can be applied to any automaton. To avoid lots of switch/case and if/then logic, each Automaton has a function pointer for its current activity (current_state_rule), which can be overwritten any time.
Each Automaton also has a list of neighbor Automata (their memory addresses), and weights for each of these neighbors. Thus, you can distance-weight the neighbors (so that corner elements are farther away), and very generalized neighbor models are possible (e.g., all lattice sites within a certain distance). When updating a cellular automaton model, such as to kill a cell, divide it, or move it, you leave the neighbor information alone, and copy/edit the information (standard_data, custom_data, current_state_rule, custom_rule). In many ways, an Automaton is just a bucket with a cell’s information in it.
Note that each Automaton also “knows” where it lives (pMicroenvironment and voxel_index), and knows what CA_Mesh it is attached to (more below).
Connecting Automata into a Lattice
An automaton by itself is lost in the world–it needs to link up into a lattice organization. Here’s where we define a CA_Mesh class, to hold the entire collection of Automata, setup functions (to match to the microenvironment), and two fundamental operations at the mesh level: copying automata (for cell division), and swapping them (for motility). We have provided two functions to accomplish these tasks, while automatically keeping the indexing and BioFVM functions correctly in sync. Here’s what it looks like:
class CA_Mesh{
private:
Microenvironment* pMicroenvironment;
Cartesian_Mesh* pMesh;
std::vector<Automaton> automata;
std::vector<int> iteration_order;
protected:
public:
CA_Mesh();
// setup to match a supplied microenvironment
void setup( Microenvironment& M );
// setup to match the default microenvironment
void setup( void );
int number_of_automata( void ) const;
void randomize_iteration_order( void );
void swap_automata( int i, int j );
void overwrite_automaton( int source_i, int destination_i );
// return the automaton sitting in the ith lattice site
Automaton& operator[]( int i );
// go through all nodes according to random shuffled order
void update_automata( double dt );
};
So, the CA_Mesh has a vector of Automata (which are never themselves moved), pointers to the microenvironment and its mesh, and a vector of automata indices that gives the iteration order (so that we can sample the automata in a random order). You can easily access an automaton with operator[], and copy the data from one Automaton to another with overwrite_automaton() (e.g, for cell division), and swap two Automata’s data (e.g., for cell migration) with swap_automata(). Finally, calling update_automata(dt) iterates through all the automata according to iteration_order, calls their current_state_rules and custom_rules, and advances the automata by dt.
Interfacing Automata with the BioFVM Microenvironment
The setup function ensures that the CA_Mesh is the same size as the Microenvironment.mesh, with same indexing, and that all automata have the correct volume, and dimension of uptake/secretion rates and parameters. If you declare and set up the Microenvironment first, all this is take care of just by declaring a CA_Mesh, as it seeks out the default microenvironment and sizes itself accordingly:
// declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // declare a Cellular_Automaton_Mesh CA_Mesh CA_model; // it's already good to go, initialized to empty automata: CA_model.display();
If you for some reason declare the CA_Mesh fist, you can set it up against the microenvironment:
// declare a CA_Mesh CA_Mesh CA_model; // declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // initialize the CA_Mesh to match the microenvironment CA_model.setup( M ); // it's already good to go, initialized to empty automata: CA_model.display();
Because each Automaton is in the microenvironment and inherits functions from Basic_Agent, it can secrete or uptake. For example, we can use functions like this one:
void set_uptake( Automaton& A, std::vector<double>& uptake_rates )
{
extern double BioFVM_CA_diffusion_dt;
// update the uptake_rates in the standard_data
A.standard_data.uptake_rates = uptake_rates;
// now, transfer them to the underlying Basic_Agent
*(A.uptake_rates) = A.standard_data.uptake_rates;
// and make sure the internal constants are self-consistent
A.set_internal_uptake_constants( BioFVM_CA_diffusion_dt );
}
A function acting on an automaton can sample the microenvironment to change parameters and state. For example:
void do_nothing( Automaton& A, double dt )
{ return; }
void microenvironment_based_rule( Automaton& A, double dt )
{
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// if pO2 < 5 mmHg, set the cell to a necrotic state
if( MS[0] < 5.0 ) { A.become_necrotic(); } // if drug > 5 uM, set the birth rate to zero
if( MS[1] > 5 )
{ A.standard_data.birth_rate = 0.0; }
// set the custom rule to something else
A.custom_rule = do_nothing;
return;
}
Implementing the mathematical model in this framework
We give each tumor cell a tumor_cell_rule (using this for custom_rule):
void viable_tumor_rule( Automaton& A, double dt )
{
// If there's no cell here, don't bother.
if( A.standard_data.state_code == BioFVM_CA_empty )
{ return; }
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// integrate drug exposure
A.standard_data.integrated_drug_exposure += ( MS[1]*dt );
A.standard_data.drug_response_function_value = pow( A.standard_data.integrated_drug_exposure,
A.standard_data.drug_hill_exponent );
double temp = pow( A.standard_data.drug_half_max_drug_exposure,
A.standard_data.drug_hill_exponent );
temp += A.standard_data.drug_response_function_value;
A.standard_data.drug_response_function_value /= temp;
// update birth rates (which themselves update probabilities)
update_birth_rate( A, MS, dt );
update_apoptotic_death_rate( A, MS, dt );
update_necrotic_death_rate( A, MS, dt );
return;
}
The functional tumor birth and death rates are implemented as:
void update_birth_rate( Automaton& A, std::vector<double>& MS, double dt )
{
static double O2_denominator = BioFVM_CA_physioxic_O2 - BioFVM_CA_necrotic_O2;
A.standard_data.birth_rate = A.standard_data.drug_response_function_value;
// response
A.standard_data.birth_rate *= A.standard_data.drug_max_birth_inhibition;
// inhibition*response;
A.standard_data.birth_rate *= -1.0;
// - inhibition*response
A.standard_data.birth_rate += 1.0;
// 1 - inhibition*response
A.standard_data.birth_rate *= viable_tumor_cell.birth_rate;
// birth_rate0*(1 - inhibition*response)
double temp1 = MS[0] ; // O2
temp1 -= BioFVM_CA_necrotic_O2;
temp1 /= O2_denominator;
A.standard_data.birth_rate *= temp1;
if( A.standard_data.birth_rate < 0 )
{ A.standard_data.birth_rate = 0.0; }
A.standard_data.probability_of_division = A.standard_data.birth_rate;
A.standard_data.probability_of_division *= dt;
// dt*birth_rate*(1 - inhibition*repsonse) // linearized probability
return;
}
void update_apoptotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.apoptotic_death_rate = A.standard_data.drug_max_death_rate;
// max_rate
A.standard_data.apoptotic_death_rate -= viable_tumor_cell.apoptotic_death_rate;
// max_rate - background_rate
A.standard_data.apoptotic_death_rate *= A.standard_data.drug_response_function_value;
// (max_rate-background_rate)*response
A.standard_data.apoptotic_death_rate += viable_tumor_cell.apoptotic_death_rate;
// background_rate + (max_rate-background_rate)*response
A.standard_data.probability_of_apoptotic_death = A.standard_data.apoptotic_death_rate;
A.standard_data.probability_of_apoptotic_death *= dt;
// dt*( background_rate + (max_rate-background_rate)*response ) // linearized probability
return;
}
void update_necrotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.necrotic_death_rate = 0.0;
A.standard_data.probability_of_necrotic_death = 0.0;
if( MS[0] > BioFVM_CA_necrotic_O2 )
{ return; }
A.standard_data.necrotic_death_rate = perinecrotic_tumor_cell.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death = A.standard_data.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death *= dt;
// dt*necrotic_death_rate
return;
}
And each fluid voxel (Dirichlet nodes) is implemented as the following (to turn on therapy at 21 days):
void fluid_rule( Automaton& A, double dt )
{
static double activation_time = 504;
static double activation_dose = 5.0;
static std::vector<double> activated_dirichlet( 2 , BioFVM_CA_physioxic_O2 );
static bool initialized = false;
if( !initialized )
{
activated_dirichlet[1] = activation_dose;
initialized = true;
}
if( fabs( BioFVM_CA_elapsed_time - activation_time ) < 0.01 ) { int ind = A.get_voxel_index(); if( A.get_microenvironment()->mesh.voxels[ind].is_Dirichlet )
{
A.get_microenvironment()->update_dirichlet_node( ind, activated_dirichlet );
}
}
}
At the start of the simulation, each non-cell automaton has its custom_rule set to fluid_rule, and each tumor cell Automaton has its custom_rule set to viable_tumor_rule. Here’s how:
void setup_cellular_automata_model( Microenvironment& M, CA_Mesh& CAM )
{
// Fill in this environment
double tumor_radius = 150;
double tumor_radius_squared = tumor_radius * tumor_radius;
std::vector<double> tumor_center( 3, 0.0 );
std::vector<double> dirichlet_value( 2 , 1.0 );
dirichlet_value[0] = 38; //physioxia
dirichlet_value[1] = 0; // drug
for( int i=0 ; i < M.number_of_voxels() ;i++ )
{
std::vector<double> displacement( 3, 0.0 );
displacement = M.mesh.voxels[i].center;
displacement -= tumor_center;
double r2 = norm_squared( displacement );
if( r2 > tumor_radius_squared ) // well_mixed_fluid
{
M.add_dirichlet_node( i, dirichlet_value );
CAM[i].copy_parameters( well_mixed_fluid );
CAM[i].custom_rule = fluid_rule;
CAM[i].current_state_rule = do_nothing;
}
else // tumor
{
CAM[i].copy_parameters( viable_tumor_cell );
CAM[i].custom_rule = viable_tumor_rule;
CAM[i].current_state_rule = advance_live_state;
}
}
}
Overall program loop
There are two inherent time scales in this problem: cell processes like division and death (happen on the scale of hours), and transport (happens on the order of minutes). We take advantage of this by defining two step sizes:
double BioFVM_CA_dt = 3; std::string BioFVM_CA_time_units = "hr"; double BioFVM_CA_save_interval = 12; double BioFVM_CA_max_time = 24*28; double BioFVM_CA_elapsed_time = 0.0; double BioFVM_CA_diffusion_dt = 0.05; std::string BioFVM_CA_transport_time_units = "min"; double BioFVM_CA_diffusion_max_time = 5.0;
Every time the simulation advances by BioFVM_CA_dt (on the order of hours), we run diffusion to quasi-steady state (for BioFVM_CA_diffusion_max_time, on the order of minutes), using time steps of size BioFVM_CA_diffusion time. We performed numerical stability and convergence analyses to determine 0.05 min works pretty well for regular lattice arrangements of cells, but you should always perform your own testing!
Here’s how it all looks, in a main program loop:
BioFVM_CA_elapsed_time = 0.0;
double next_output_time = BioFVM_CA_elapsed_time; // next time you save data
while( BioFVM_CA_elapsed_time < BioFVM_CA_max_time + 1e-10 )
{
// if it's time, save the simulation
if( fabs( BioFVM_CA_elapsed_time - next_output_time ) < BioFVM_CA_dt/2.0 )
{
std::cout << "simulation time: " << BioFVM_CA_elapsed_time << " " << BioFVM_CA_time_units
<< " (" << BioFVM_CA_max_time << " " << BioFVM_CA_time_units << " max)" << std::endl;
char* filename;
filename = new char [1024];
sprintf( filename, "output_%6f" , next_output_time );
save_BioFVM_cellular_automata_to_MultiCellDS_xml_pugi( filename , M , CA_model ,
BioFVM_CA_elapsed_time );
cell_counts( CA_model );
delete [] filename;
next_output_time += BioFVM_CA_save_interval;
}
// do the cellular automaton step
CA_model.update_automata( BioFVM_CA_dt );
BioFVM_CA_elapsed_time += BioFVM_CA_dt;
// simulate biotransport to quasi-steady state
double t_diffusion = 0.0;
while( t_diffusion < BioFVM_CA_diffusion_max_time + 1e-10 )
{
M.simulate_diffusion_decay( BioFVM_CA_diffusion_dt );
M.simulate_cell_sources_and_sinks( BioFVM_CA_diffusion_dt );
t_diffusion += BioFVM_CA_diffusion_dt;
}
}
Getting and Running the Code
- Start a project: Create a new directory for your project (I’d recommend “BioFVM_CA_tumor”), and enter the directory. Place a copy of BioFVM (the zip file) into your directory. Unzip BioFVM, and copy BioFVM*.h, BioFVM*.cpp, and pugixml* files into that directory.
- Download the demo source code: Download the source code for this tutorial: BioFVM_CA_Example_1, version 1.0.0 or later. Unzip its contents into your project directory. Go ahead and overwrite the Makefile.
- Edit the makefile (if needed): Note that if you are using OSX, you’ll probably need to change from “g++” to your installed compiler. See these tutorials.
- Test the code: Go to a command line (see previous tutorials), and test:
make ./BioFVM_CA_Example_1
(If you’re on windows, run BioFVM_CA_Example_1.exe.)
Simulation Result
If you run the code to completion, you will simulate 3 weeks of in vitro growth, followed by a bolus “injection” of drug. The code will simulate one one additional week under the drug. (This should take 5-10 minutes, including full simulation saves every 12 hours.)
In matlab, you can load a saved dataset and check the minimum oxygenation value like this:
MCDS = read_MultiCellDS_xml( 'output_504.000000.xml' ); min(min(min( MCDS.continuum_variables(1).data )))
And then you can start visualizing like this:
contourf( MCDS.mesh.X_coordinates , MCDS.mesh.Y_coordinates , ...
MCDS.continuum_variables(1).data(:,:,33)' ) ;
axis image;
colorbar
xlabel('x (\mum)' , 'fontsize' , 12 );
ylabel( 'y (\mum)' , 'fontsize', 12 );
set(gca, 'fontsize', 12 );
title('Oxygenation (mmHg) at z = 0 \mum', 'fontsize', 14 );
print('-dpng', 'Tumor_o2_3_weeks.png' );
plot_cellular_automata( MCDS , 'Tumor spheroid at 3 weeks');
Simulation plots
Here are some plots, showing (left from right) pO2 concentration, a cross-section of the tumor (red = live cells, green = apoptotic, and blue = necrotic), and the drug concentration (after start of therapy):
1 week:
Oxygen- and space-limited growth are restricted to the outer boundary of the tumor spheroid.
2 weeks:
Oxygenation is dipped below 5 mmHg in the center, leading to necrosis.
3 weeks:
As the tumor grows, the hypoxic gradient increases, and the necrotic core grows. The code turns on a constant 5 micromolar dose of doxorubicin at this point
Treatment + 12 hours:
The drug has started to penetrate the tumor, triggering apoptotic death towards the outer periphery where exposure has been greatest.
Treatment + 24 hours:
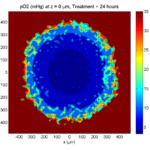
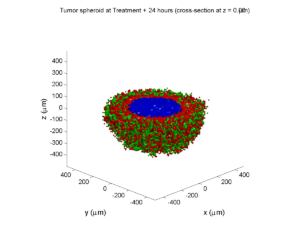
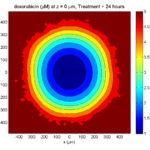
The drug profile hasn’t changed much, but the interior cells have now had greater exposure to drug, and hence greater response. Now apoptosis is observed throughout the non-necrotic tumor. The tumor has decreased in volume somewhat.
Treatment + 36 hours:
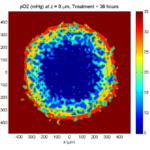
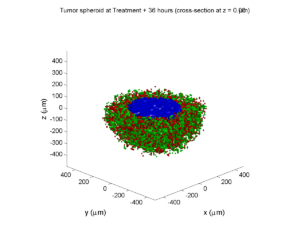
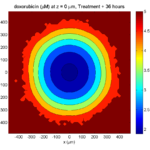
The non-necrotic tumor is now substantially apoptotic. We would require some pharamcokinetic effects (e.g., drug clearance, inactivation, or removal) to avoid the inevitable, presences of a pre-existing resistant strain, or emergence of resistance.
Treatment + 48 hours:
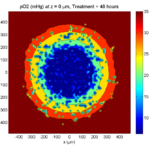
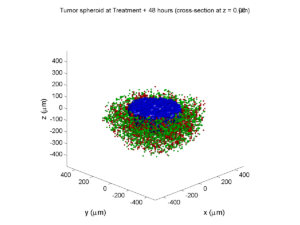
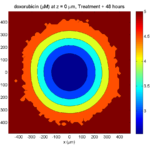
By now, almost all cells are apoptotic.
Treatment + 60 hours:

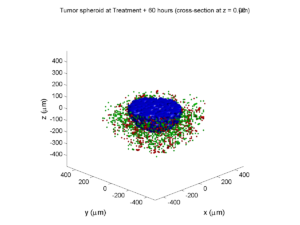
The non-necrotic tumor is nearly completed eliminated, leaving a leftover core of previously-necrotic cells (which did not change state in response to the drug–they were already dead!)
Source files
You can download completed source for this example here: https://sourceforge.net/projects/biofvm/files/Tutorials/Cellular_Automaton_1/
This file will include the following:
- BioFVM_cellular_automata.h
- BioFVM_cellular_automata.cpp
- BioFVM_CA_example_1.cpp
- read_MultiCellDS_xml.m (updated)
- plot_cellular_automata.m
- Makefile
What’s next
I plan to update this source code with extra cell motility, and potentially more realistic parameter values. Also, I plan to more formally separate out the example from the generic cell capabilities, so that this source code can work as a bona fide cellular automaton framework.
More immediately, my next tutorial will use the reverse strategy: start with an existing cellular automaton model, and integrate BioFVM capabilities.
Return to News • Return to MathCancer • Follow @MathCancer
BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations
I’m very excited to announce that our 3-D diffusion solver has been accepted for publication and is now online at Bioinformatics. Click here to check out the open access preprint!
A. Ghaffarizadeh, S.H. Friedman, and P. Macklin. BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations. Bioinformatics, 2015.
DOI: 10.1093/bioinformatics/btv730 (free; open access)
BioFVM (stands for “Finite Volume Method for biological problems) is an open source package to solve for 3-D diffusion of several substrates with desktop workstations, single supercomputer nodes, or even laptops (for smaller problems). We built it from the ground up for biological problems, with optimizations in C++ and OpenMP to take advantage of all those cores on your CPU. The code is available at SourceForge and BioFVM.MathCancer.org.
The main idea here is to make it easier to simulate big, cool problems in 3-D multicellular biology. We’ll take care of secretion, diffusion, and uptake of things like oxygen, glucose, metabolic waste products, signaling factors, and drugs, so you can focus on the rest of your model.
Design philosophy and main capabilities
Solving diffusion equations efficiently and accurately is hard, especially in 3D. Almost all biological simulations deal with this, many by using explicit finite differences (easy to code and accurate, but very slow!) or implicit methods like ADI (accurate and relatively fast, but difficult to code with complex linking to libraries). While real biological systems often depend upon many diffusing things (lots of signaling factors for cell-cell communication, growth substrates, drugs, etc.), most solvers only scale well to simulating two or three. We solve a system of PDEs of the following form:
\[ \frac{\partial \vec{\rho}}{\partial t} = \overbrace{ \vec{D} \nabla^2 \vec{\rho} }^\textrm{diffusion}
– \overbrace{ \vec{\lambda} \vec{\rho} }^\textrm{decay} + \overbrace{ \vec{S} \left( \vec{\rho}^* – \vec{\rho} \right) }^{\textrm{bulk source}} – \overbrace{ \vec{U} \vec{\rho} }^{\textrm{bulk uptake}} + \overbrace{\sum_{\textrm{cells } k} 1_k(\vec{x}) \left[ \vec{S}_k \left( \vec{\rho}^*_k – \vec{\rho} \right) – \vec{U}_k \vec{\rho} \right] }^\textrm{sources and sinks by cells} \]
Above, all vector-vector products are term-by-term.
Solving for many diffusing substrates
We set out to write a package that could simulate many diffusing substrates using algorithms that were fast but simple enough to optimize. To do this, we wrote the entire solver to work on vectors of substrates, rather than on individual PDEs. In performance testing, we found that simulating 10 diffusing things only takes about 2.6 times longer than simulating one. (In traditional codes, simulating ten things takes ten times as long as simulating one.) We tried our hardest to break the code in our testing, but we failed. We simulated all the way from 1 diffusing substrate up to 128 without any problems. Adding new substrates increases the computational cost linearly.
Combining simple but tailored solvers
We used an approach called operator splitting: breaking a complicated PDE into a series of simpler PDEs and ODEs, which can be solved one at a time with implicit methods. This allowed us to write a very fast diffusion/decay solver, a bulk supply/uptake solver, and a cell-based secretion/uptake solver. Each of these individual solvers was individually optimized. Theory tells us that if each individual solver is first-order accurate in time and stable, then the overall approach is first-order accurate in time and stable.
The beauty of the approach is that each solver can individually be improved over time. For example, in BioFVM 1.0.2, we doubled the performance of the cell-based secretion/uptake solver. The operator splitting approach also lets us add new terms to the “main” PDE by writing new solvers, rather than rewriting a large, monolithic solver. We will take advantage of this to add advective terms (critical for interstitial flow) in future releases.
Optimizing the diffusion solver for large 3-D domains
For the first main release of BioFVM, we restricted ourselves to Cartesian meshes, which allowed us to write very tailored mesh data structures and diffusion solvers. (Note: the finite volume method reduces to finite differences on Cartesian meshes with trivial Neumann boundary conditions.) We intend to work on more general Voronoi meshes in a future release. (This will be particularly helpful for sources/sinks along blood vessels.)
By using constant diffusion and decay coefficients, we were able to write very fast solvers for Cartesian meshes. We use the locally one-dimensional (LOD) method–a specialized form of operator splitting–to break the 3-D diffusion problem into a series of 1-D diffusion problems. For each (y,z) in our mesh, we have a 1-D diffusion problem along x. This yields a tridiagonal linear system which we can solve efficiently with the Thomas algorithm. Moreover, because the forward-sweep steps only depend upon the coefficient matrix (which is unchanging over time), we can pre-compute and store the results in memory for all the x-diffusion problems. In fact, the structure of the matrix allows us to pre-compute part of the back-substitution steps as well. Same for y- and z-diffusion. This gives a big speedup.
Next, we can use all those CPU cores to speed up our work. While the back-substitution steps of the Thomas algorithm can’t be easily parallelized (it’s a serial operation), we can solve many x-diffusion problems at the same time, using independent copies (instances) of the Thomas solver. So, we break up all the x-diffusion problems up across a big OpenMP loop, and repeat for y– and z-diffusion.
Lastly, we used overloaded +=, axpy and similar operations on the vector of substrates, to avoid unnecessary (and very expensive) memory allocation and copy operations wherever we could. This was a really fun code to write!
The work seems to have payed off: we have found that solving on 1 million voxel meshes (about 8 mm3 at 20 μm resolution) is easy even for laptops.
Simulating many cells
We tailored the solver to allow both lattice- and off-lattice cell sources and sinks. Desktop workstations should have no trouble with 1,000,000 cells secreting and uptaking a few substrates.
Simplifying the non-science
We worked to minimize external dependencies, because few things are more frustrating than tracking down a bunch of libraries that may not work together on your platform. The first release BioFVM only has one external dependency: pugixml (an XML parser). We didn’t link an entire linear algebra library just to get axpy and a Thomas solver–it wouldn’t have been optimized for our system anyway. We implemented what we needed of the freely available .mat file specification, rather than requiring a separate library for that. (We have used these matlab read/write routines in house for several years.)
Similarly, we stuck to a very simple mesh data structure so we wouldn’t have to maintain compatibility with general mesh libraries (which can tend to favor feature sets and generality over performance and simplicity). Rather than use general-purpose ODE solvers (with yet more library dependencies, and more work for maintaining compatibility), we wrote simple solvers tailored specifically to our equations.
The upshot of this is that you don’t have to do anything fancy to replicate results with BioFVM. Just grab a copy of the source, drop it into your project directory, include it in your project (e.g., your makefile), and you’re good to go.
All the juicy details
The Bioinformatics paper is just 2 pages long, using the standard “Applications Note” format. It’s a fantastic format for announcing and disseminating a piece of code, and we’re grateful to be published there. But you should pop open the supplementary materials, because all the fun mathematics are there:
- The full details of the numerical algorithm, including information on our optimizations.
- Convergence tests: For several examples, we showed:
- First-order convergence in time (with respect to Δt), and stability
- Second-order convergence in space (with respect to Δx)
- Accuracy tests: For each convergence test, we looked at how small Δt has to be to ensure 5% relative accuracy at Δx = 20 μm resolution. For oxygen-like problems with cell-based sources and sinks, Δt = 0.01 min will do the trick. This is about 15 times larger than the stability-restricted time step for explicit methods.
- Performance tests:
- Computational cost (wall time to simulate a fixed problem on a fixed domain size with fixed time/spatial resolution) increases linearly with the number of substrates. 5-10 substrates are very feasible on desktop workstations.
- Computational cost increases linearly with the number of voxels
- Computational cost increases linearly in the number of cell-based source/sinks
And of course because this code is open sourced, you can dig through the implementation details all you like! (And improvements are welcome!)
What’s next?
- As MultiCellDS (multicellular data standard) matures, we will implement read/write support for <microenvironment> data in digital snapshots.
- We have a few ideas to improve the speed of the cell-based sources and sinks. In particular, switching to a higher-order accurate solver may allow larger time step sizes, so long as the method is still stable. For the specific form of the sources/sinks, the trapezoid rule could work well here.
- I’d like to allow a spatially-varying diffusion coefficient. We could probably do this (at very great memory cost) by writing separate Thomas solvers for each strip in x, y, and z, or by giving up the pre-computation part of the optimization. I’m still mulling this one over.
- I’d also like to implement non-Cartesian meshes. The data structure isn’t a big deal, but we lose the LOD optimization and Thomas solvers. In this case, we’d either use explicit methods (very slow!), use an iterative matrix solver (trickier to parallelize nicely, except in matrix-vector multiplication operations), or start with quasi-steady problems that let us use Gauss-Seidel iterative type methods, like this old paper.
- Since advective flow (particularly interstitial flow) is so important for many problems, I’d like to add an advective solver. This will require some sort of upwinding to maintain stability.
- At some point, we’d like to port this to GPUs. However, I don’t currently have time / resources to maintain a separate CUDA or OpenCL branch. (Perhaps this will be an excuse to learn Julia on GPUs.)
Well, we hope you find BioFVM useful. If you give it a shot, I’d love to hear back from you!
Very best — Paul
Macklin Lab featured on March 2013 cover of Notices of the American Mathematical Society
I’m very excited to be featured on this month’s cover of the Notices of the American Mathematical Society. The cover shows a series of images from a multiscale simulation of a tumor growing in the brain, made with John Lowengrub while I was a Ph.D. student at UC Irvine. (See Frieboes et al. 2007, Macklin et al. 2009, and Macklin and Lowengrub 2008.) The “about the cover” write-up (Page 325) gives more detail.
The inside has a short interview on our more current work, particularly 3-D agent-based modeling. You should also read Rick Durrett‘s perspective piece on cancer modeling (Page 304)—it’s a great read! (And yup, Figure 3 is from our patient-calibrated breast cancer modeling in Macklin et al. 2012. ;-) )
The entire March 2013 issue can be accessed for free at the AMS Notices website:
http://www.ams.org/notices/201303/
I want to thank Bill Casselman and Rick Durrett for making this possible. I had a lot of fun in the process, and I’m grateful for the opportunity to trade ideas!