Category: matlab
Working with PhysiCell MultiCellDS digital snapshots in Matlab
PhysiCell 1.2.1 and later saves data as a specialized MultiCellDS digital snapshot, which includes chemical substrate fields, mesh information, and a readout of the cells and their phenotypes at single simulation time point. This tutorial will help you learn to use the matlab processing files included with PhysiCell.
This tutorial assumes you know (1) how to work at the shell / command line of your operating system, and (2) basic plotting and other functions in Matlab.
Key elements of a PhysiCell digital snapshot
A PhysiCell digital snapshot (a customized form of the MultiCellDS digital simulation snapshot) includes the following elements saved as XML and MAT files:
- output12345678.xml : This is the “base” output file, in MultiCellDS format. It includes key metadata such as when the file was created, the software, microenvironment information, and custom data saved at the simulation time. The Matlab files read this base file to find other related files (listed next). Example: output00003696.xml
- initial_mesh0.mat : This is the computational mesh information for BioFVM at time 0.0. Because BioFVM and PhysiCell do not use moving meshes, we do not save this data at any subsequent time.
- output12345678_microenvironment0.mat : This saves each biochemical substrate in the microenvironment at the computational voxels defined in the mesh (see above). Example: output00003696_microenvironment0.mat
- output12345678_cells.mat : This saves very basic cellular information related to BioFVM, including cell positions, volumes, secretion rates, uptake rates, and secretion saturation densities. Example: output00003696_cells.mat
- output12345678_cells_physicell.mat : This saves extra PhysiCell data for each cell agent, including volume information, cell cycle status, motility information, cell death information, basic mechanics, and any user-defined custom data. Example: output00003696_cells_physicell.mat
These snapshots make extensive use of Matlab Level 4 .mat files, for fast, compact, and well-supported saving of array data. Note that even if you cannot ready MultiCellDS XML files, you can work to parse the .mat files themselves.
The PhysiCell Matlab .m files
Every PhysiCell distribution includes some matlab functions to work with PhysiCell digital simulation snapshots, stored in the matlab subdirectory. The main ones are:
- composite_cutaway_plot.m : provides a quick, coarse 3-D cutaway plot of the discrete cells, with different colors for live (red), apoptotic (b), and necrotic (black) cells.
- read_MultiCellDS_xml.m : reads the “base” PhysiCell snapshot and its associated matlab files.
- set_MCDS_constants.m : creates a data structure MCDS_constants that has the same constants as PhysiCell_constants.h. This is useful for identifying cell cycle phases, etc.
- simple_cutaway_plot.m : provides a quick, coarse 3-D cutaway plot of user-specified cells.
- simple_plot.m : provides, a quick, coarse 3-D plot of the user-specified cells, without a cutaway or cross-sectional clipping plane.
A note on GNU Octave
Unfortunately, GNU octave does not include XML file parsing without some significant user tinkering. And one you’re done, it is approximately one order of magnitude slower than Matlab. Octave users can directly import the .mat files described above, but without the helpful metadata in the XML file. We’ll provide more information on the structure of these MAT files in a future blog post. Moreover, we plan to provide python and other tools for users without access to Matlab.
A sample digital snapshot
We provide a 3-D simulation snapshot from the final simulation time of the cancer-immune example in Ghaffarizadeh et al. (2017, in review) at:
The corresponding SVG cross-section for that time (through z = 0 μm) looks like this:
Unzip the sample dataset in any directory, and make sure the matlab files above are in the same directory (or in your Matlab path). If you’re inside matlab:
!unzip 3D_PhysiCell_matlab_sample.zip
Loading a PhysiCell MultiCellDS digital snapshot
Now, load the snapshot:
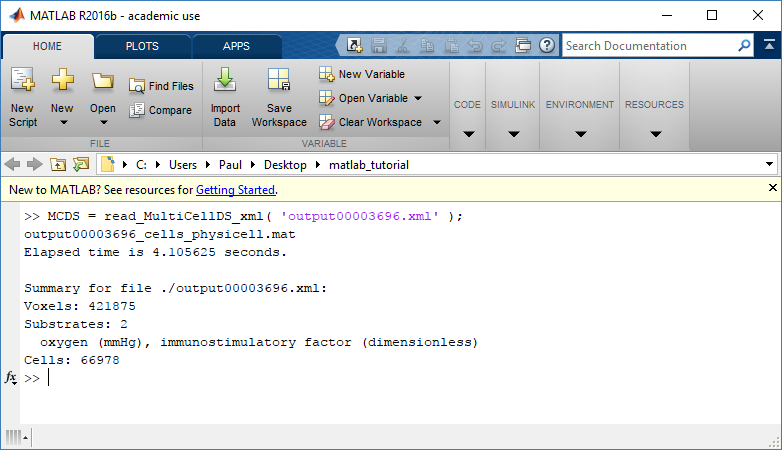
MCDS = read_MultiCellDS_xml( 'output00003696.xml');
This will load the mesh, substrates, and discrete cells into the MCDS data structure, and give a basic summary:
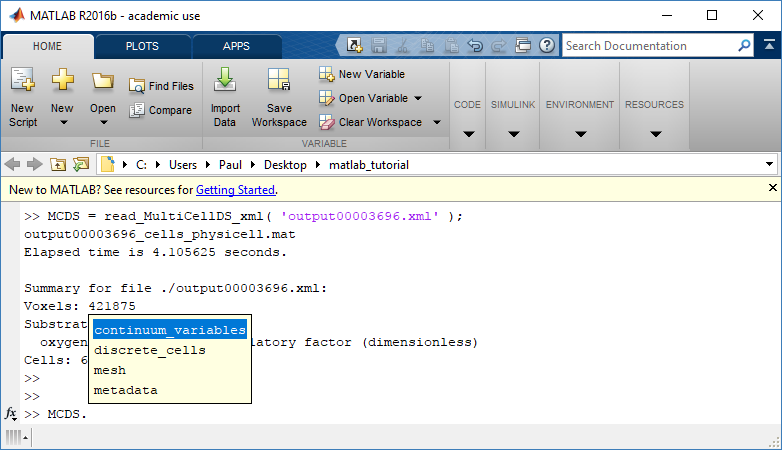
Typing ‘MCDS’ and then hitting ‘tab’ (for auto-completion) shows the overall structure of MCDS, stored as metadata, mesh, continuum variables, and discrete cells:
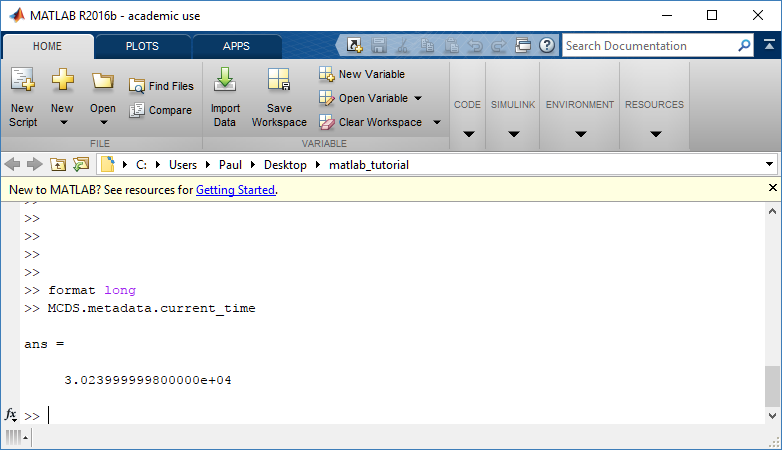
To get simulation metadata, such as the current simulation time, look at MCDS.metadata.current_time
Here, we see that the current simulation time is 30240 minutes, or 21 days. MCDS.metadata.current_runtime gives the elapsed walltime to up to this point: about 53 hours (1.9e5 seconds), including file I/O time to write full simulation data once per 3 simulated minutes after the start of the adaptive immune response.
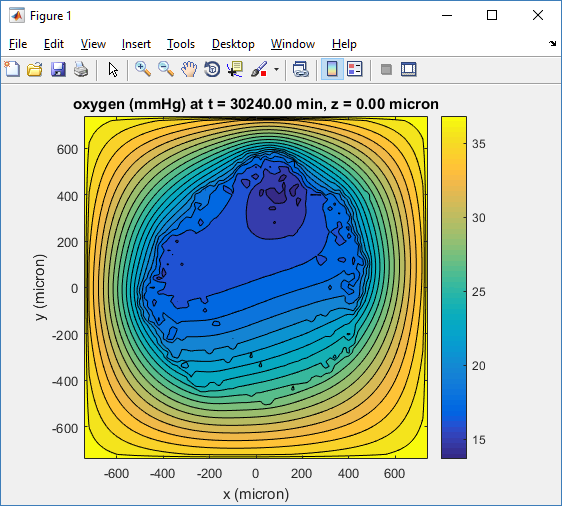
Plotting chemical substrates
Let’s make an oxygen contour plot through z = 0 μm. First, we find the index corresponding to this z-value:
k = find( MCDS.mesh.Z_coordinates == 0 );
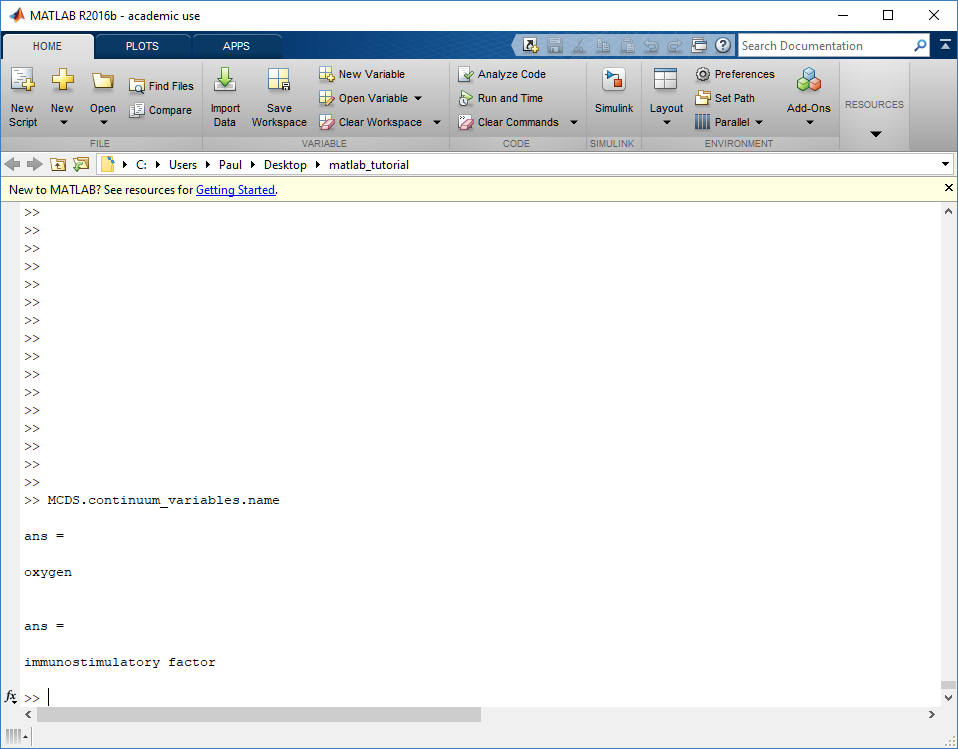
Next, let’s figure out which variable is oxygen. Type “MCDS.continuum_variables.name”, which will show the array of variable names:
Here, oxygen is the first variable, (index 1). So, to make a filled contour plot:
contourf( MCDS.mesh.X(:,:,k), MCDS.mesh.Y(:,:,k), ...
MCDS.continuum_variables(1).data(:,:,k) , 20 ) ;
Now, let’s set this to a correct aspect ratio (no stretching in x or y), add a colorbar, and set the axis labels, using
metadata to get labels:
axis image colorbar xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) ); ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
Lastly, let’s add an appropriate (time-based) title:
title( sprintf('%s (%s) at t = %3.2f %s, z = %3.2f %s', MCDS.continuum_variables(1).name , ...
MCDS.continuum_variables(1).units , ...
MCDS.metadata.current_time , ...
MCDS.metadata.time_units, ...
MCDS.mesh.Z_coordinates(k), ...
MCDS.metadata.spatial_units ) );
Here’s the end result:
We can easily export graphics, such as to PNG format:
print( '-dpng' , 'output_o2.png' );
For more on plotting BioFVM data, see the tutorial
at http://www.mathcancer.org/blog/saving-multicellds-data-from-biofvm/
Plotting cells in space
3-D point cloud
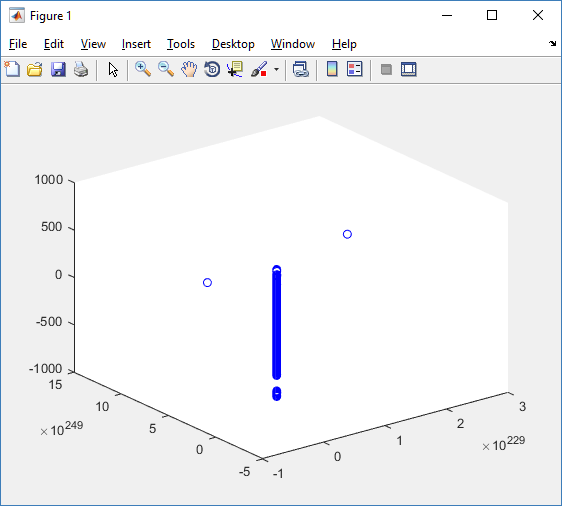
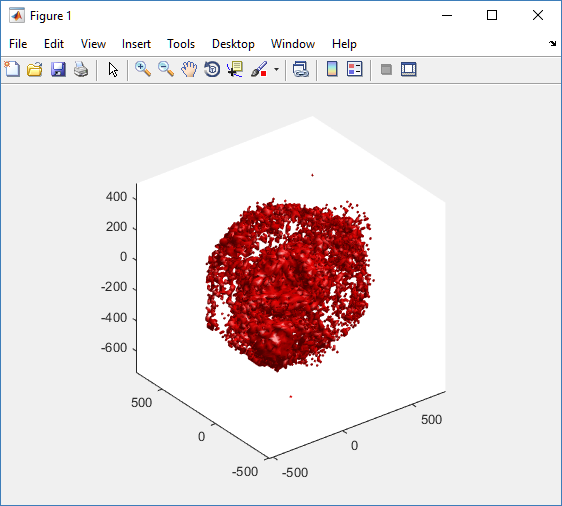
First, let’s plot all the cells in 3D:
plot3( MCDS.discrete_cells.state.position(:,1) , MCDS.discrete_cells.state.position(:,2), ... MCDS.discrete_cells.state.position(:,3) , 'bo' );
At first glance, this does not look good: some cells are far out of the simulation domain, distorting the automatic range of the plot:
This does not ordinarily happen in PhysiCell (the default cell mechanics functions have checks to prevent such behavior), but this example includes a simple Hookean elastic adhesion model for immune cell attachment to tumor cells. In rare circumstances, an attached tumor cell or immune cell can apoptose on its own (due to its background apoptosis rate),
without “knowing” to detach itself from the surviving cell in the pair. The remaining cell attempts to calculate its elastic velocity based upon an invalid cell position (no longer in memory), creating an artificially large velocity that “flings” it out of the simulation domain. Such cells are not simulated any further, so this is effectively equivalent to an extra apoptosis event (only 3 cells are out of the simulation domain after tens of millions of cell-cell elastic adhesion calculations). Future versions of this example will include extra checks to prevent this rare behavior.
The plot can simply be fixed by changing the axis:
axis( 1000*[-1 1 -1 1 -1 1] ) axis square
Notice that this is a very difficult plot to read, and very non-interactive (laggy) to rotation and scaling operations. We can make a slightly nicer plot by searching for different cell types and plotting them with different colors:
% make it easier to work with the cell positions;
P = MCDS.discrete_cells.state.position;
% find type 1 cells
ind1 = find( MCDS.discrete_cells.metadata.type == 1 );
% better still, eliminate those out of the simulation domain
ind1 = find( MCDS.discrete_cells.metadata.type == 1 & ...
abs(P(:,1))' < 1000 & abs(P(:,2))' < 1000 & abs(P(:,3))' < 1000 );
% find type 0 cells
ind0 = find( MCDS.discrete_cells.metadata.type == 0 & ...
abs(P(:,1))' < 1000 & abs(P(:,2))' < 1000 & abs(P(:,3))' < 1000 );
%now plot them
P = MCDS.discrete_cells.state.position;
plot3( P(ind0,1), P(ind0,2), P(ind0,3), 'bo' )
hold on
plot3( P(ind1,1), P(ind1,2), P(ind1,3), 'ro' )
hold off
axis( 1000*[-1 1 -1 1 -1 1] )
axis square
However, this isn’t much better. You can use the scatter3 function to gain more control on the size and color of the plotted cells, or even make macros to plot spheres in the cell locations (with shading and lighting), but Matlab is very slow when plotting beyond 103 cells. Instead, we recommend the faster preview functions below for data exploration, and higher-quality plotting (e.g., by POV-ray) for final publication-
Fast 3-D cell data previewers
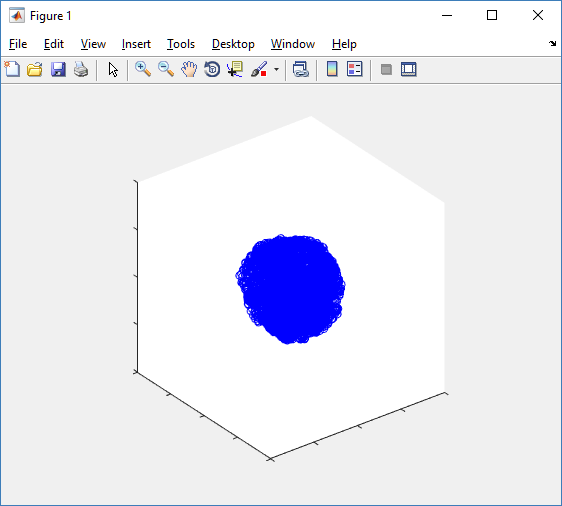
Notice that plot3 and scatter3 are painfully slow for any nontrivial number of cells. We can use a few fast previewers to quickly get a sense of the data. First, let’s plot all the dead cells, and make them red:
clf simple_plot( MCDS, MCDS, MCDS.discrete_cells.dead_cells , 'r' )
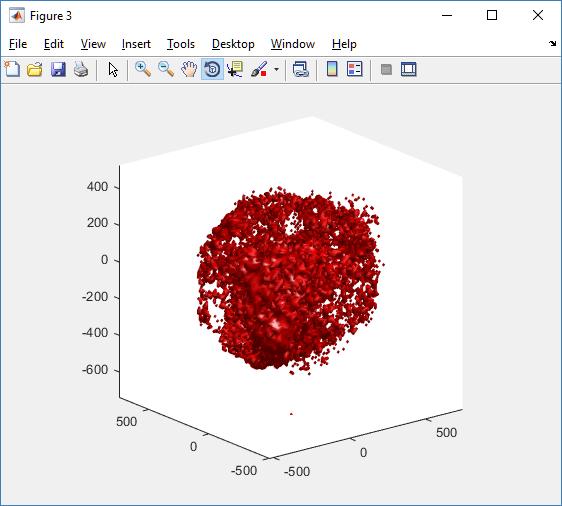
This function creates a coarse-grained 3-D indicator function (0 if no cells are present; 1 if they are), and plots a 3-D level surface. It is very responsive to rotations and other operations to explore the data. You may notice the second argument is a list of indices: only these cells are plotted. This gives you a method to select cells with specific characteristics when plotting. (More on that below.) If you want to get a sense of the interior structure, use a cutaway plot:
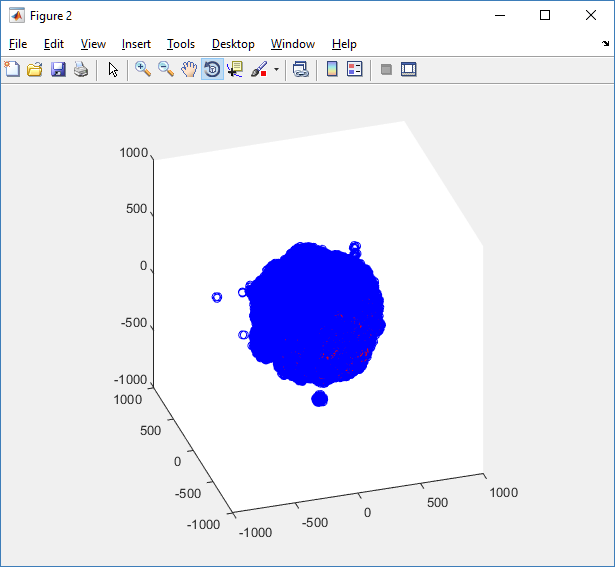
clf simple_cutaway_plot( MCDS, MCDS, MCDS.discrete_cells.dead_cells , 'r' )
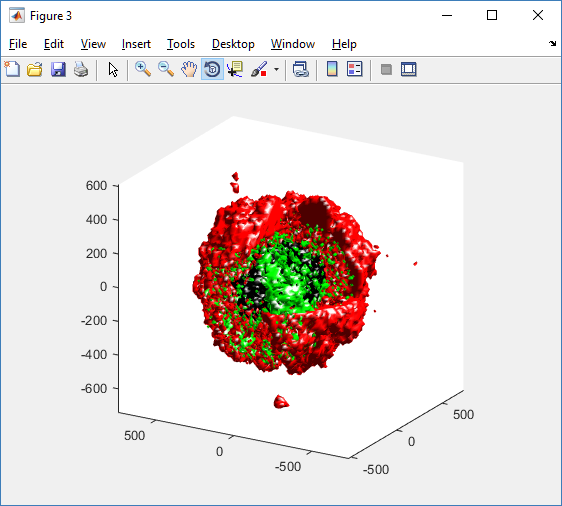
We also provide a fast “composite” cutaway which plots all live cells as red, apoptotic cells as blue (without the cutaway), and all necrotic cells as black:
clf composite_cutaway_plot( MCDS )

Lastly, we show an improved plot that uses different colors for the immune cells, and Matlab’s “find” function to help set up the indexing:
constants = set_MCDS_constants
% find the type 0 necrotic cells
ind0_necrotic = find( MCDS.discrete_cells.metadata.type == 0 & ...
(MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic_swelling | ...
MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic_lysed | ...
MCDS.discrete_cells.phenotype.cycle.current_phase == constants.necrotic) );
% find the live type 0 cells
ind0_live = find( MCDS.discrete_cells.metadata.type == 0 & ...
(MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic_swelling & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic_lysed & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.necrotic & ...
MCDS.discrete_cells.phenotype.cycle.current_phase ~= constants.apoptotic) );
clf
% plot live tumor cells red, in cutaway view
simple_cutaway_plot( MCDS, ind0_live , 'r' );
hold on
% plot dead tumor cells black, in cutaway view
simple_cutaway_plot( MCDS, ind0_necrotic , 'k' )
% plot all immune cells, but without cutaway (to show how they infiltrate)
simple_plot( MCDS, ind1, 'g' )
hold off
A small cautionary note on future compatibility
PhysiCell 1.2.1 uses the <custom> data tag (allowed as part of the MultiCellDS specification) to encode its cell data, to allow a more compact data representation, because the current PhysiCell daft does not support such a formulation, and Matlab is painfully slow at parsing XML files larger than ~50 MB. Thus, PhysiCell snapshots are not yet fully compatible with general MultiCellDS tools, which would by default ignore custom data. In the future, we will make available converter utilities to transform “native” custom PhysiCell snapshots to MultiCellDS snapshots that encode all the cellular information in a more verbose but compatible XML format.
Closing words and future work
Because Octave is not a great option for parsing XML files (with critical MultiCellDS metadata), we plan to write similar functions to read and plot PhysiCell snapshots in Python, as an open source alternative. Moreover, our lab in the next year will focus on creating further MultiCellDS configuration, analysis, and visualization routines. We also plan to provide additional 3-D functions for plotting the discrete cells and varying color with their properties.
In the longer term, we will develop open source, stand-alone analysis and visualization tools for MultiCellDS snapshots (including PhysiCell snapshots). Please stay tuned!
A small computational thought experiment
In Macklin (2017), I briefly touched on a simple computational thought experiment that shows that for a group of homogeneous cells, you can observe substantial heterogeneity in cell behavior. This “thought experiment” is part of a broader preview and discussion of a fantastic paper by Linus Schumacher, Ruth Baker, and Philip Maini published in Cell Systems, where they showed that a migrating collective homogeneous cells can show heterogeneous behavior when quantitated with new migration metrics. I highly encourage you to check out their work!
In this blog post, we work through my simple thought experiment in a little more detail.
Note: If you want to reference this blog post, please cite the Cell Systems preview article:
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
The thought experiment
Consider a simple (and widespread) model of a population of cycling cells: each virtual cell (with index i) has a single “oncogene” \( r_i \) that sets the rate of progression through the cycle. Between now (t) and a small time from now ( \(t+\Delta t\)), the virtual cell has a probability \(r_i \Delta t\) of dividing into two daughter cells. At the population scale, the overall population growth model that emerges from this simple single-cell model is:
\[\frac{dN}{dt} = \langle r\rangle N, \]
where \( \langle r \rangle \) the mean division rate over the cell population, and N is the number of cells. See the discussion in the supplementary information for Macklin et al. (2012).
Now, suppose (as our thought experiment) that we could track individual cells in the population and track how long it takes them to divide. (We’ll call this the division time.) What would the distribution of cell division times look like, and how would it vary with the distribution of the single-cell rates \(r_i\)?
Mathematical method
In the Matlab script below, we implement this cell cycle model as just about every discrete model does. Here’s the pseudocode:
t = 0;
while( t < t_max )
for i=1:Cells.size()
u = random_number();
if( u < Cells[i].birth_rate * dt )
Cells[i].division_time = Cells[i].age;
Cells[i].divide();
end
end
t = t+dt;
end
That is, until we’ve reached the final simulation time, loop through all the cells and decide if they should divide: For each cell, choose a random number between 0 and 1, and if it’s smaller than the cell’s division probability (\(r_i \Delta t\)), then divide the cell and write down the division time.
As an important note, we have to track the same cells until they all divide, rather than merely record which cells have divided up to the end of the simulation. Otherwise, we end up with an observational bias that throws off our recording. See more below.
The sample code
You can download the Matlab code for this example at:
http://MathCancer.org/files/matlab/thought_experiment_matlab(Macklin_Cell_Systems_2017).zip
Extract all the files, and run “thought_experiment” in Matlab (or Octave, if you don’t have a Matlab license or prefer an open source platform) for the main result.
All these Matlab files are available as open source, under the GPL license (version 3 or later).
Results and discussion
First, let’s see what happens if all the cells are identical, with \(r = 0.05 \textrm{ hr}^{-1}\). We run the script, and track the time for each of 10,000 cells to divide. As expected by theory (Macklin et al., 2012) (but perhaps still a surprise if you haven’t looked), we get an exponential distribution of division times, with mean time \(1/\langle r \rangle\):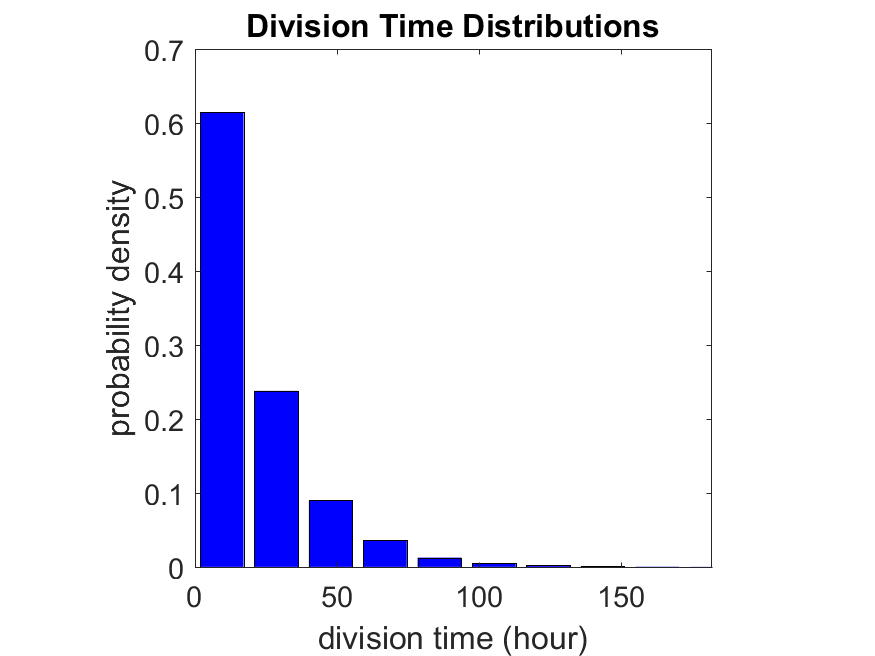
So even in this simple model, a homogeneous population of cells can show heterogeneity in their behavior. Here’s the interesting thing: let’s now give each cell its own division parameter \(r_i\) from a normal distribution with mean \(0.05 \textrm{ hr}^{-1}\) and a relative standard deviation of 25%: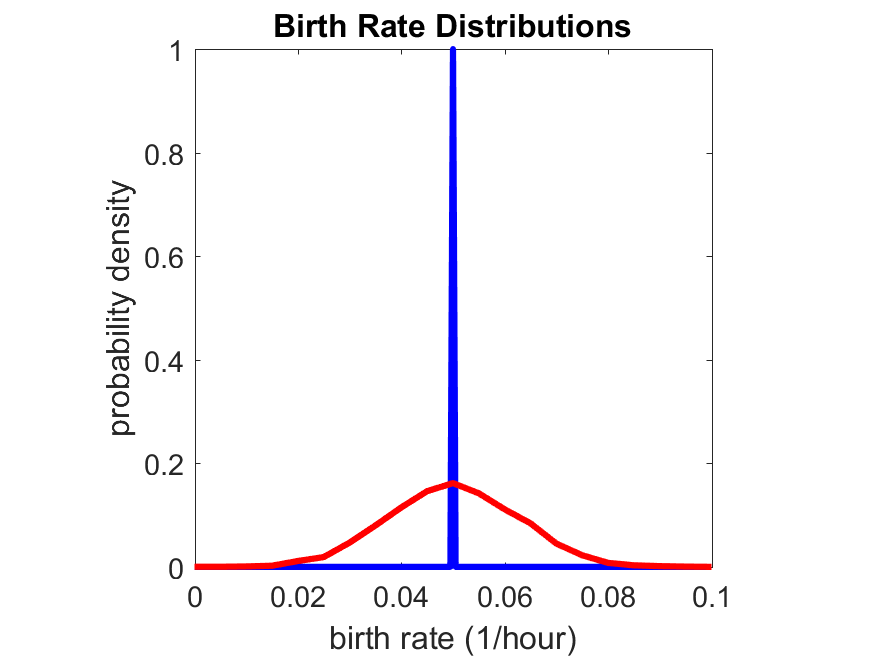
If we repeat the experiment, we get the same distribution of cell division times!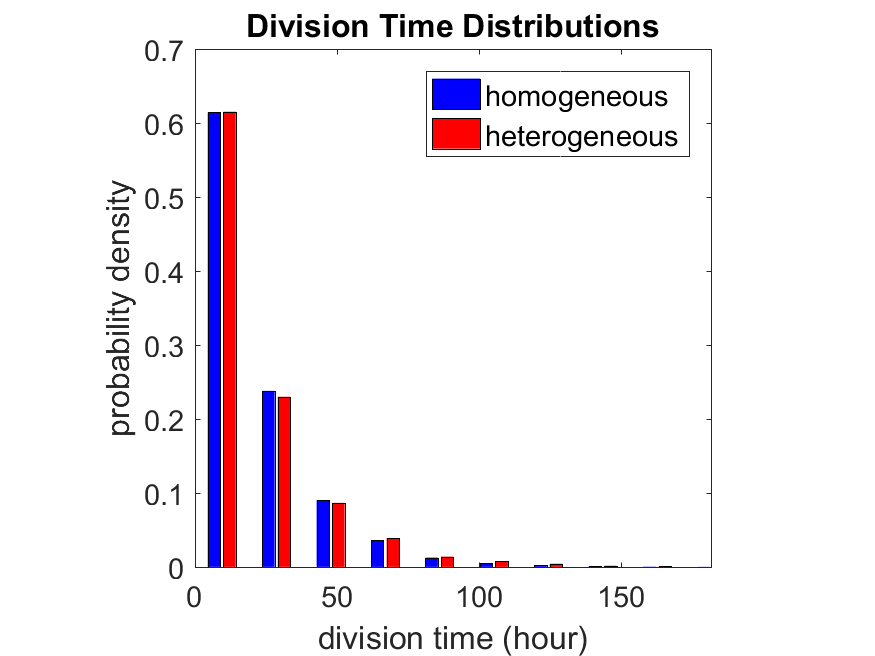
So in this case, based solely on observations of the phenotypic heterogeneity (the division times), it is impossible to distinguish a “genetically” homogeneous cell population (one with identical parameters) from a truly heterogeneous population. We would require other metrics, like tracking changes in the mean division time as cells with a higher \(r_i\) out-compete the cells with lower \(r_i\).
Lastly, I want to point out that caution is required when designing these metrics and single-cell tracking. If instead we had tracked all cells throughout the simulated experiment, including new daughter cells, and then recorded the first 10,000 cell division events, we would get a very different distribution of cell division times: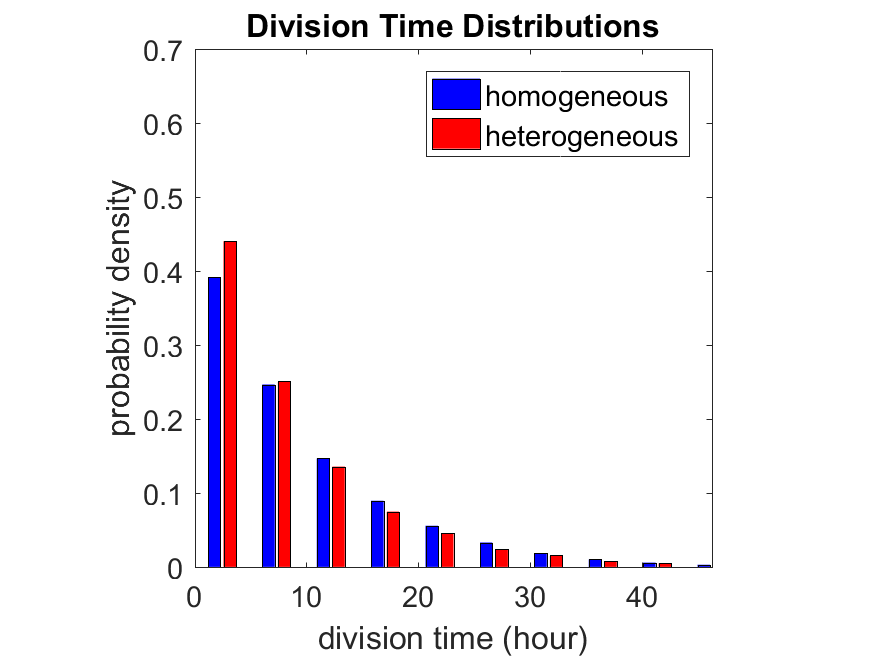
By only recording the division times for the cells that have divided, and not those that haven’t, we bias our observations towards cells with shorter division times. Indeed, the mean division time for this simulated experiment is far lower than we would expect by theory. You can try this one by running “bad_thought_experiment”.
Further reading
This post is an expansion of our recent preview in Cell Systems in Macklin (2017):
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
And the original work on apparent heterogeneity in collective cell migration is by Schumacher et al. (2017):
L. Schumacher et al., Semblance of Heterogeneity in Collective Cell Migration. Cell Sys., 2017 (in press). DOI: 10.1016/j.cels.2017.06.006
You can read some more on relating exponential distributions and Poisson processes to common discrete mathematical models of cell populations in Macklin et al. (2012):
P. Macklin, et al., Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 301:122-40, 2012. DOI: 10.1016/j.jtbi.2012.02.002.
Lastly, I’d be delighted if you took a look at the open source software we have been developing for 3-D simulations of multicellular systems biology:
http://OpenSource.MathCancer.org
And you can always keep up-to-date by following us on Twitter: @MathCancer.
Coarse-graining discrete cell cycle models

Introduction
One observation that often goes underappreciated in computational biology discussions is that a computational model is often a model of a model of a model of biology: that is, it’s a numerical approximation (a model) of a mathematical model of an experimental model of a real-life biological system. Thus, there are three big places where a computational investigation can fall flat:
- The experimental model may be a bad choice for the disease or process (not our fault).
- Second, the mathematical model of the experimental system may have flawed assumptions (something we have to evaluate).
- The numerical implementation may have bugs or otherwise be mathematically inconsistent with the mathematical model.
Critically, you can’t use simulations to evaluate the experimental model or the mathematical model until you verify that the numerical implementation is consistent with the mathematical model, and that the numerical solution converges as \( \Delta t\) and \( \Delta x \) shrink to zero.
There are numerous ways to accomplish this, but ideally, it boils down to having some analytical solutions to the mathematical model, and comparing numerical solutions to these analytical or theoretical results. In this post, we’re going to walk through the math of analyzing a typical type of discrete cell cycle model.
Discrete model
Suppose we have a cell cycle model consisting of phases \(P_1, P_2, \ldots P_n \), where cells in the \(P_i\) phase progress to the \(P_{i+1}\) phase after a mean waiting time of \(T_i\), and cells leaving the \(P_n\) phase divide into two cells in the \(P_1\) phase. Assign each cell agent \(k\) a current phenotypic phase \( S_k(t) \). Suppose also that each phase \( i \) has a death rate \( d_i \), and that cells persist for on average \( T_\mathrm{A} \) time in the dead state before they are removed from the simulation.
The mean waiting times \( T_i \) are equivalent to transition rates \( r_i = 1 / T_i \) (Macklin et al. 2012). Moreover, for any time interval \( [t,t+\Delta t] \), both are equivalent to a transition probability of
\[ \mathrm{Prob}\Bigl( S_k(t+\Delta t) = P_{i+1} | S(t) = P_i \Bigr) = 1 – e^{ -r_i \Delta t } \approx r_i \Delta t = \frac{ \Delta t}{ T_i}. \] In many discrete models (especially cellular automaton models) with fixed step sizes \( \Delta t \), models are stated in terms of transition probabilities \( p_{i,i+1} \), which we see are equivalent to the work above with \( p_{i,i+1} = r_i \Delta t = \Delta t / T_i \), allowing us to tie mathematical model forms to biological, measurable parameters. We note that each \(T_i\) is the average duration of the \( P_i \) phase.
Concrete example: a Ki67 Model
Ki-67 is a nuclear protein that is expressed through much of the cell cycle, including S, G2, M, and part of G1 after division. It is used very commonly in pathology to assess proliferation, particularly in cancer. See the references and discussion in (Macklin et al. 2012). In Macklin et al. (2012), we came up with a discrete cell cycle model to match Ki-67 data (along with cleaved Caspase-3 stains for apoptotic cells). Let’s summarize the key parts here.
Each cell agent \(i\) has a phase \(S_i(t)\). Ki67- cells are quiescent (phase \(Q\), mean duration \( T_\mathrm{Q} \)), and they can enter the Ki67+ \(K_1\) phase (mean duration \(T_1\)). When \( K_1 \) cells leave their phase, they divide into two Ki67+ daughter cells in the \( K_2 \) phase with mean duration \( T_2 \). When cells exit \( K_2 \), they return to \( Q \). Cells in any phase can become apoptotic (enter the \( A \) phase with mean duration \( T_\mathrm{A} \)), with death rate \( r_\mathrm{A} \).
Coarse-graining to an ODE model
If each phase \(i\) has a death rate \(d_i\), if \( N_i(t) \) denotes the number of cells in the \( P_i \) phase at time \( t\), and if \( A(t) \) is the number of dead (apoptotic) cells at time \( t\), then on average, the number of cells in the \( P_i \) phase at the next time step is given by
\[ N_i(t+\Delta t) = N_i(t) + N_{i-1}(t) \cdot \left[ \textrm{prob. of } P_{i-1} \rightarrow P_i \textrm{ transition} \right] – N_i(t) \cdot \left[ \textrm{prob. of } P_{i} \rightarrow P_{i+1} \textrm{ transition} \right] \] \[ – N_i(t) \cdot \left[ \textrm{probability of death} \right] \] By the work above, this is:
\[ N_i(t+\Delta t) \approx N_i(t) + N_{i-1}(t) r_{i-1} \Delta t – N_i(t) r_i \Delta t – N_i(t) d_i \Delta t , \] or after shuffling terms and taking the limit as \( \Delta t \downarrow 0\), \[ \frac{d}{dt} N_i(t) = r_{i-1} N_{i-1}(t) – \left( r_i + d_i \right) N_i(t). \] Continuing this analysis, we obtain a linear system:
\[ \frac{d}{dt}{ \vec{N} } = \begin{bmatrix} -(r_1+d_1) & 0 & \cdots & 0 & 2r_n & 0 \\ r_1 & -(r_2+d_2) & 0 & \cdots & 0 & 0 \\ 0 & r_2 & -(r_3+d_3) & 0 & \cdots & 0 \\ & & \ddots & & \\0&\cdots&0 &r_{n-1} & -(r_n+d_n) & 0 \\ d_1 & d_2 & \cdots & d_{n-1} & d_n & -\frac{1}{T_\mathrm{A}} \end{bmatrix}\vec{N} = M \vec{N}, \] where \( \vec{N}(t) = [ N_1(t), N_2(t) , \ldots , N_n(t) , A(t) ] \).
For the Ki67 model above, let \(\vec{N} = [K_1, K_2, Q, A]\). Then the linear system is
\[ \frac{d}{dt} \vec{N} = \begin{bmatrix} -\left( \frac{1}{T_1} + r_\mathrm{A} \right) & 0 & \frac{1}{T_\mathrm{Q}} & 0 \\ \frac{2}{T_1} & -\left( \frac{1}{T_2} + r_\mathrm{A} \right) & 0 & 0 \\ 0 & \frac{1}{T_2} & -\left( \frac{1}{T_\mathrm{Q}} + r_\mathrm{A} \right) & 0 \\ r_\mathrm{A} & r_\mathrm{A} & r_\mathrm{A} & -\frac{1}{T_\mathrm{A}} \end{bmatrix} \vec{N} .\]
(If we had written \( \vec{N} = [Q, K_1, K_2 , A] \), then the matrix above would have matched the general form.)
Some theoretical results
If \( M\) has eigenvalues \( \lambda_1 , \ldots \lambda_{n+1} \) and corresponding eigenvectors \( \vec{v}_1, \ldots , \vec{v}_{n+1} \), then the general solution is given by
\[ \vec{N}(t) = \sum_{i=1}^{n+1} c_i e^{ \lambda_i t } \vec{v}_i ,\] and if the initial cell counts are given by \( \vec{N}(0) \) and we write \( \vec{c} = [c_1, \ldots c_{n+1} ] \), we can obtain the coefficients by solving \[ \vec{N}(0) = [ \vec{v}_1 | \cdots | \vec{v}_{n+1} ]\vec{c} .\] In many cases, it turns out that all but one of the eigenvalues (say \( \lambda \) with corresponding eigenvector \(\vec{v}\)) are negative. In this case, all the other components of the solution decay away, and for long times, we have \[ \vec{N}(t) \approx c e^{ \lambda t } \vec{v} .\] This is incredibly useful, because it says that over long times, the fraction of cells in the \( i^\textrm{th} \) phase is given by \[ v_{i} / \sum_{j=1}^{n+1} v_{j}. \]
Matlab implementation (with the Ki67 model)
First, let’s set some parameters, to make this a little easier and reusable.
parameters.dt = 0.1; % 6 min = 0.1 hours parameters.time_units = 'hour'; parameters.t_max = 3*24; % 3 days parameters.K1.duration = 13; parameters.K1.death_rate = 1.05e-3; parameters.K1.initial = 0; parameters.K2.duration = 2.5; parameters.K2.death_rate = 1.05e-3; parameters.K2.initial = 0; parameters.Q.duration = 74.35 ; parameters.Q.death_rate = 1.05e-3; parameters.Q.initial = 1000; parameters.A.duration = 8.6; parameters.A.initial = 0;
Next, we write a function to read in the parameter values, construct the matrix (and all the data structures), find eigenvalues and eigenvectors, and create the theoretical solution. It also finds the positive eigenvalue to determine the long-time values.
function solution = Ki67_exact( parameters )
% allocate memory for the main outputs
solution.T = 0:parameters.dt:parameters.t_max;
solution.K1 = zeros( 1 , length(solution.T));
solution.K2 = zeros( 1 , length(solution.T));
solution.K = zeros( 1 , length(solution.T));
solution.Q = zeros( 1 , length(solution.T));
solution.A = zeros( 1 , length(solution.T));
solution.Live = zeros( 1 , length(solution.T));
solution.Total = zeros( 1 , length(solution.T));
% allocate memory for cell fractions
solution.AI = zeros(1,length(solution.T));
solution.KI1 = zeros(1,length(solution.T));
solution.KI2 = zeros(1,length(solution.T));
solution.KI = zeros(1,length(solution.T));
% get the main parameters
T1 = parameters.K1.duration;
r1A = parameters.K1.death_rate;
T2 = parameters.K2.duration;
r2A = parameters.K2.death_rate;
TQ = parameters.Q.duration;
rQA = parameters.Q.death_rate;
TA = parameters.A.duration;
% write out the mathematical model:
% d[Populations]/dt = Operator*[Populations]
Operator = [ -(1/T1 +r1A) , 0 , 1/TQ , 0; ...
2/T1 , -(1/T2 + r2A) ,0 , 0; ...
0 , 1/T2 , -(1/TQ + rQA) , 0; ...
r1A , r2A, rQA , -1/TA ];
% eigenvectors and eigenvalues
[V,D] = eig(Operator);
eigenvalues = diag(D);
% save the eigenvectors and eigenvalues in case you want them.
solution.V = V;
solution.D = D;
solution.eigenvalues = eigenvalues;
% initial condition
VecNow = [ parameters.K1.initial ; parameters.K2.initial ; ...
parameters.Q.initial ; parameters.A.initial ] ;
solution.K1(1) = VecNow(1);
solution.K2(1) = VecNow(2);
solution.Q(1) = VecNow(3);
solution.A(1) = VecNow(4);
solution.K(1) = solution.K1(1) + solution.K2(1);
solution.Live(1) = sum( VecNow(1:3) );
solution.Total(1) = sum( VecNow(1:4) );
solution.AI(1) = solution.A(1) / solution.Total(1);
solution.KI1(1) = solution.K1(1) / solution.Total(1);
solution.KI2(1) = solution.K2(1) / solution.Total(1);
solution.KI(1) = solution.KI1(1) + solution.KI2(1);
% now, get the coefficients to write the analytic solution
% [Populations] = c1*V(:,1)*exp( d(1,1)*t) + c2*V(:,2)*exp( d(2,2)*t ) +
% c3*V(:,3)*exp( d(3,3)*t) + c4*V(:,4)*exp( d(4,4)*t );
coeff = linsolve( V , VecNow );
% find the (hopefully one) positive eigenvalue.
% eigensolutions with negative eigenvalues decay,
% leaving this as the long-time behavior.
eigenvalues = diag(D);
n = find( real( eigenvalues ) &gt; 0 )
solution.long_time.KI1 = V(1,n) / sum( V(:,n) );
solution.long_time.KI2 = V(2,n) / sum( V(:,n) );
solution.long_time.QI = V(3,n) / sum( V(:,n) );
solution.long_time.AI = V(4,n) / sum( V(:,n) ) ;
solution.long_time.KI = solution.long_time.KI1 + solution.long_time.KI2;
% now, write out the solution at all the times
for i=2:length( solution.T )
% compact way to write the solution
VecExact = real( V*( coeff .* exp( eigenvalues*solution.T(i) ) ) );
solution.K1(i) = VecExact(1);
solution.K2(i) = VecExact(2);
solution.Q(i) = VecExact(3);
solution.A(i) = VecExact(4);
solution.K(i) = solution.K1(i) + solution.K2(i);
solution.Live(i) = sum( VecExact(1:3) );
solution.Total(i) = sum( VecExact(1:4) );
solution.AI(i) = solution.A(i) / solution.Total(i);
solution.KI1(i) = solution.K1(i) / solution.Total(i);
solution.KI2(i) = solution.K2(i) / solution.Total(i);
solution.KI(i) = solution.KI1(i) + solution.KI2(i);
end
return;
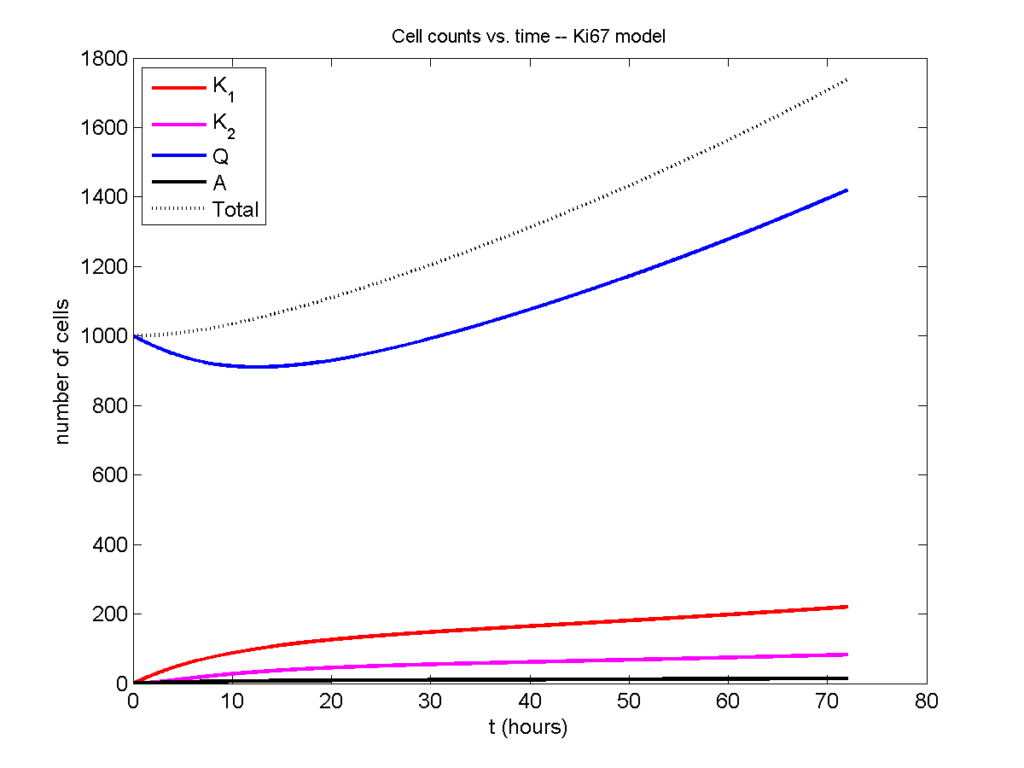
Now, let’s run it and see what this thing looks like:
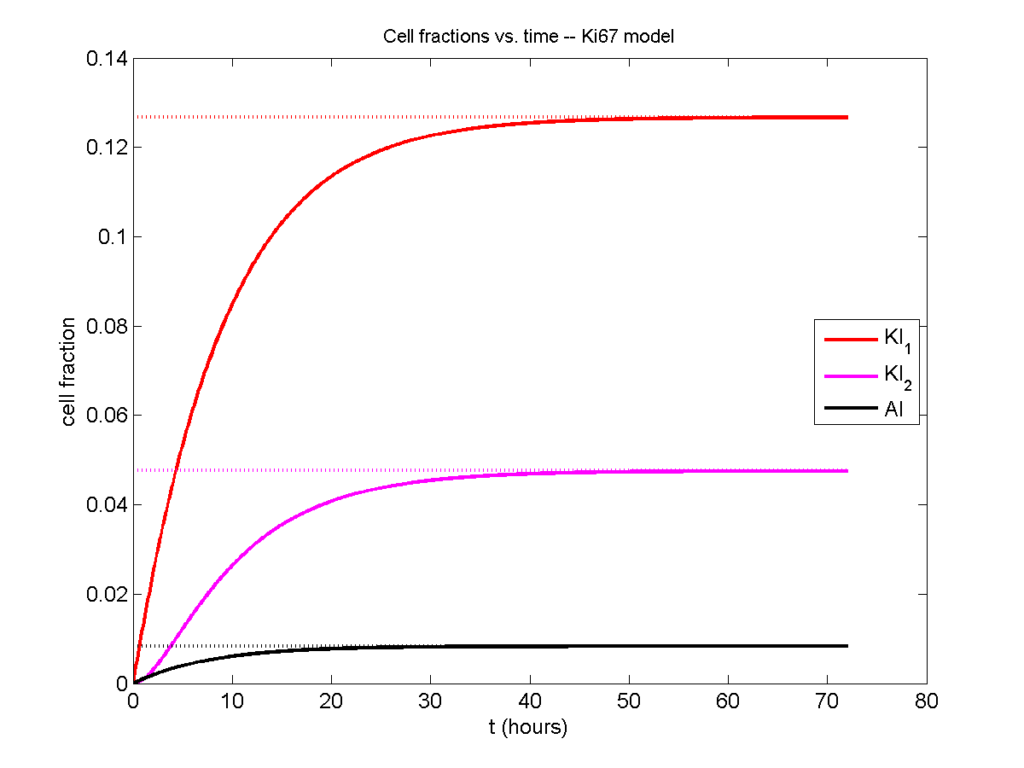
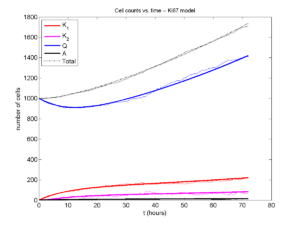
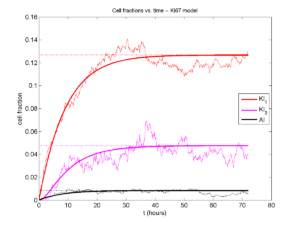
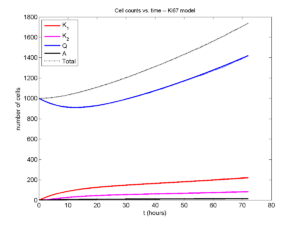
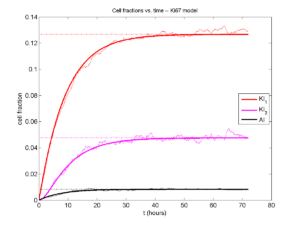
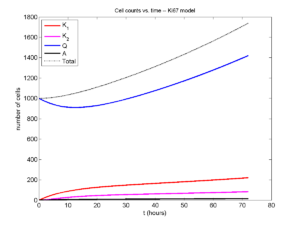
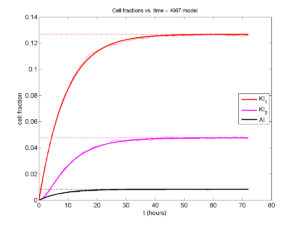
Next, we plot KI1, KI2, and AI versus time (solid curves), along with the theoretical long-time behavior (dashed curves). Notice how well it matches–it’s neat when theory works! :-)
Some readers may recognize the long-time fractions: KI1 + KI2 = KI = 0.1743, and AI = 0.00833, very close to the DCIS patient values from our simulation study in Macklin et al. (2012) and improved calibration work in Hyun and Macklin (2013).
Comparing simulations and theory
I wrote a small Matlab program to implement the discrete model: start with 1000 cells in the \(Q\) phase, and in each time interval \([t,t+\Delta t]\), each cell “decides” whether to advance to the next phase, stay in the same phase, or apoptose. If we compare a single run against the theoretical curves, we see hints of a match:
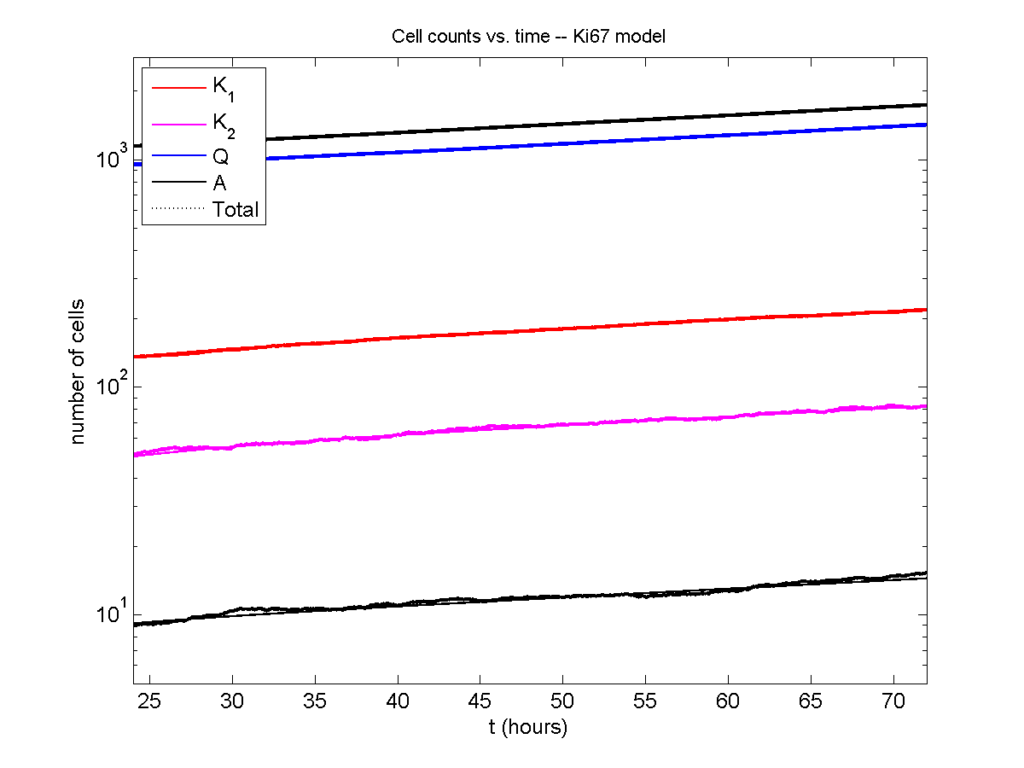
If we average 10 simulations and compare, the match is better:
And lastly, if we average 100 simulations and compare, the curves are very difficult to tell apart:
Even in logarithmic space, it’s tough to tell these apart:
Code
The following matlab files (available here) can be used to reproduce this post:
- Ki67_exact.m
- The function defined above to create the exact solution using the eigenvalue/eignvector approach.
- Ki67_stochastic.m
- Runs a single stochastic simulation, using the supplied parameters.
- script.m
- Runs the theoretical solution first, creates plots, and then runs the stochastic model 100 times for comparison.
To make it all work, simply run “script” at the command prompt. Please note that it will generate some png files in its directory.
Closing thoughts
In this post, we showed a nice way to check a discrete model against theoretical behavior–both in short-term dynamics and long-time behavior. The same work should apply to validating many discrete models. However, when you add spatial effects (e.g., a cellular automaton model that won’t proliferate without an empty neighbor site), I wouldn’t expect a match. (But simulating cells that initially have a “salt and pepper”, random distribution should match this for early times.)
Moreover, models with deterministic phase durations (e.g., K1, K2, and A have fixed durations) aren’t consistent with the ODE model above, unless the cells they are each initialized with a random amount of “progress” in their initial phases. (Otherwise, the cells in each phase will run synchronized, and there will be fixed delays before cells transition to other phases.) Delay differential equations better describe such models. However, for long simulation times, the slopes of the sub-populations and the cell fractions should start to better and better match the ODE models.
Now that we have verified that the discrete model is performing as expected, we can have greater confidence in its predictions, and start using those predictions to assess the underlying models. In ODE and PDE models, you often validate the code on simpler problems where you have an analytical solution, and then move on to making simulation predictions in cases where you can’t solve analytically. Similarly, we can now move on to variants of the discrete model where we can’t as easily match ODE theory (e.g., time-varying rate parameters, spatial effects), but with the confidence that the phase transitions are working as they should.
Saving MultiCellDS data from BioFVM
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM.
Introduction
A major initiative for my lab has been MultiCellDS: a standard for multicellular data. The project aims to create model-neutral representations of simulation data (for both discrete and continuum models), which can also work for segmented experimental and clinical data. A single-time output is called a digital snapshot. An interdisciplinary, multi-institutional review panel has been hard at work to nail down the draft standard.
A BioFVM MultiCellDS digital snapshot includes program and user metadata (more information to be included in a forthcoming publication), an output of the microenvironment, and any cells that are secreting or uptaking substrates.
As of Version 1.1.0, BioFVM supports output saved to MultiCellDS XML files. Each download also includes a matlab function for importing MultiCellDS snapshots saved by BioFVM programs. This tutorial will get you going.
BioFVM (finite volume method for biological problems) is an open source code for solving 3-D diffusion of 1 or more substrates. It was recently published as open access in Bioinformatics here:
http://dx.doi.org/10.1093/bioinformatics/btv730
The project website is at http://BioFVM.MathCancer.org, and downloads are at http://BioFVM.sf.net.
Working with MultiCellDS in BioFVM programs
We include a MultiCellDS_test.cpp file in the examples directory of every BioFVM download (Version 1.1.0 or later). Create a new project directory, copy the following files to it:
- BioFVM*.cpp and BioFVM*.h (from the main BioFVM directory)
- pugixml.* (from the main BioFVM directory)
- Makefile and MultiCellDS_test.cpp (from the examples directory)
Open the MultiCellDS_test.cpp file to see the syntax as you read the rest of this post.
See earlier tutorials (below) if you have troubles with this.
Setting metadata values
There are few key bits of metadata. First, the program used for the simulation (all these fields are optional):
// the program name, version, and project website:
BioFVM_metadata.program.program_name = "BioFVM MultiCellDS Test";
BioFVM_metadata.program.program_version = "1.0";
BioFVM_metadata.program.program_URL = "http://BioFVM.MathCancer.org";
// who created the program (if known)
BioFVM_metadata.program.creator.surname = "Macklin";
BioFVM_metadata.program.creator.given_names = "Paul";
BioFVM_metadata.program.creator.email = "Paul.Macklin@usc.edu";
BioFVM_metadata.program.creator.URL = "http://BioFVM.MathCancer.org";
BioFVM_metadata.program.creator.organization = "University of Southern California";
BioFVM_metadata.program.creator.department = "Center for Applied Molecular Medicine";
BioFVM_metadata.program.creator.ORCID = "0000-0002-9925-0151";
// (generally peer-reviewed) citation information for the program
BioFVM_metadata.program.citation.DOI = "10.1093/bioinformatics/btv730";
BioFVM_metadata.program.citation.PMID = "26656933";
BioFVM_metadata.program.citation.PMCID = "PMC1234567";
BioFVM_metadata.program.citation.text = "A. Ghaffarizadeh, S.H. Friedman, and P. Macklin,
BioFVM: an efficient parallelized diffusive transport solver for 3-D biological
simulations, Bioinformatics, 2015. DOI: 10.1093/bioinformatics/btv730.";
BioFVM_metadata.program.citation.notes = "notes here";
BioFVM_metadata.program.citation.URL = "http://dx.doi.org/10.1093/bioinformatics/btv730";
// user information: who ran the program
BioFVM_metadata.program.user.surname = "Kirk";
BioFVM_metadata.program.user.given_names = "James T.";
BioFVM_metadata.program.user.email = "Jimmy.Kirk@starfleet.mil";
BioFVM_metadata.program.user.organization = "Starfleet";
BioFVM_metadata.program.user.department = "U.S.S. Enterprise (NCC 1701)";
BioFVM_metadata.program.user.ORCID = "0000-0000-0000-0000";
// And finally, data citation information (the publication where this simulation snapshot appeared)
BioFVM_metadata.data_citation.DOI = "10.1093/bioinformatics/btv730";
BioFVM_metadata.data_citation.PMID = "12345678";
BioFVM_metadata.data_citation.PMCID = "PMC1234567";
BioFVM_metadata.data_citation.text = "A. Ghaffarizadeh, S.H. Friedman, and P. Macklin, BioFVM:
an efficient parallelized diffusive transport solver for 3-D biological simulations, Bioinformatics,
2015. DOI: 10.1093/bioinformatics/btv730.";
BioFVM_metadata.data_citation.notes = "notes here";
BioFVM_metadata.data_citation.URL = "http://dx.doi.org/10.1093/bioinformatics/btv730";
You can sync the metadata current time, program runtime (wall time), and dimensional units using the following command. (This command is automatically run whenever you use the save command below.)
BioFVM_metadata.sync_to_microenvironment( M );
You can display a basic summary of the metadata via:
BioFVM_metadata.display_information( std::cout );
Setting options
By default (to save time and disk space), BioFVM saves the mesh as a Level 3 matlab file, whose location is embedded into the MultiCellDS XML file. You can disable this feature and revert to full XML (e.g., for human-readable cross-model reporting) via:
set_save_biofvm_mesh_as_matlab( false );
Similarly, BioFVM defaults to saving the values of the substrates in a compact Level 3 matlab file. You can override this with:
set_save_biofvm_data_as_matlab( false );
BioFVM by default saves the cell-centered sources and sinks. These take a lot of time to parse because they require very hierarchical data structures. You can disable saving the cells (basic_agents) via:
set_save_biofvm_cell_data( false );
Lastly, when you do save the cells, we default to a customized, minimal matlab format. You can revert to a more standard (but much larger) XML format with:
set_save_biofvm_cell_data_as_custom_matlab( false )
Saving a file
Saving the data is very straightforward:
save_BioFVM_to_MultiCellDS_xml_pugi( "sample" , M , current_simulation_time );
Your data will be saved in sample.xml. (Depending upon your options, it may generate several .mat files beginning with “sample”.)
If you’d like the filename to depend upon the simulation time, use something more like this:
double current_simulation_time = 10.347; char filename_base [1024]; sprintf( &filename_base , "sample_%f", current_simulation_time ); save_BioFVM_to_MultiCellDS_xml_pugi( filename_base , M, current_simulation_time );
Your data will be saved in sample_10.347000.xml. (Depending upon your options, it may generate several .mat files beginning with “sample_10.347000”.)
Compiling and running the program:
Edit the Makefile as below:
PROGRAM_NAME := MCDS_test all: $(BioFVM_OBJECTS) $(pugixml_OBJECTS) MultiCellDS_test.cpp $(COMPILE_COMMAND) -o $(PROGRAM_NAME) $(BioFVM_OBJECTS) $(pugixml_OBJECTS) MultiCellDS_test.cpp
If you’re running OSX, you’ll probably need to update the compiler from “g++”. See these tutorials.
Then, at the command prompt:
make ./MCDS_test
On Windows, you’ll need to run without the ./:
make MCDS_test
Working with MultiCellDS data in Matlab
Reading data in Matlab
Copy the read_MultiCellDS_xml.m file from the matlab directory (included in every MultiCellDS download). To read the data, just do this:
MCDS = read_MultiCellDS_xml( 'sample.xml' );
This should take around 30 seconds for larger data files (500,000 to 1,000,000 voxels with a few substrates, and around 250,000 cells). The long execution time is primarily because Matlab is ghastly inefficient at loops over hierarchical data structures. Increasing to 1,000,000 cells requires around 80-90 seconds to parse in matlab.
Plotting data in Matlab
Plotting the 3-D substrate data
First, let’s do some basic contour and surface plotting:
mid_index = round( length(MCDS.mesh.Z_coordinates)/2 );
contourf( MCDS.mesh.X(:,:,mid_index), ...
MCDS.mesh.Y(:,:,mid_index), ...
MCDS.continuum_variables(2).data(:,:,mid_index) , 20 ) ;
axis image
colorbar
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('%s (%s) at t = %f %s, z = %f %s', MCDS.continuum_variables(2).name , ...
MCDS.continuum_variables(2).units , ...
MCDS.metadata.current_time , ...
MCDS.metadata.time_units, ...
MCDS.mesh.Z_coordinates(mid_index), ...
MCDS.metadata.spatial_units ) );
OR
contourf( MCDS.mesh.X_coordinates , MCDS.mesh.Y_coordinates, ...
MCDS.continuum_variables(2).data(:,:,mid_index) , 20 ) ;
axis image
colorbar
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('%s (%s) at t = %f %s, z = %f %s', ...
MCDS.continuum_variables(2).name , ...
MCDS.continuum_variables(2).units , ...
MCDS.metadata.current_time , ...
MCDS.metadata.time_units, ...
MCDS.mesh.Z_coordinates(mid_index), ...
MCDS.metadata.spatial_units ) );
Here’s a surface plot:
surf( MCDS.mesh.X_coordinates , MCDS.mesh.Y_coordinates, ...
MCDS.continuum_variables(1).data(:,:,mid_index) ) ;
colorbar
axis tight
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
zlabel( sprintf( '%s (%s)', MCDS.continuum_variables(1).name, ...
MCDS.continuum_variables(1).units ) );
title( sprintf('%s (%s) at t = %f %s, z = %f %s', MCDS.continuum_variables(1).name , ...
MCDS.continuum_variables(1).units , ...
MCDS.metadata.current_time , ...
MCDS.metadata.time_units, ...
MCDS.mesh.Z_coordinates(mid_index), ...
MCDS.metadata.spatial_units ) );
Finally, here are some more advanced plots. The first is an “exploded” stack of contour plots:
clf
contourslice( MCDS.mesh.X , MCDS.mesh.Y, MCDS.mesh.Z , ...
MCDS.continuum_variables(2).data , [],[], ...
MCDS.mesh.Z_coordinates(1:15:length(MCDS.mesh.Z_coordinates)),20);
view([-45 10]);
axis tight;
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
zlabel( sprintf( 'z (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('%s (%s) at t = %f %s', ...
MCDS.continuum_variables(2).name , ...
MCDS.continuum_variables(2).units , ...
MCDS.metadata.current_time, ...
MCDS.metadata.time_units ) );
Next, we show how to use isosurfaces with transparency
clf
patch( isosurface( MCDS.mesh.X , MCDS.mesh.Y, MCDS.mesh.Z, ...
MCDS.continuum_variables(1).data, 1000 ), 'edgecolor', ...
'none', 'facecolor', 'r' , 'facealpha' , 1 );
hold on
patch( isosurface( MCDS.mesh.X , MCDS.mesh.Y, MCDS.mesh.Z, ...
MCDS.continuum_variables(1).data, 5000 ), 'edgecolor', ...
'none', 'facecolor', 'b' , 'facealpha' , 0.7 );
patch( isosurface( MCDS.mesh.X , MCDS.mesh.Y, MCDS.mesh.Z, ...
MCDS.continuum_variables(1).data, 10000 ), 'edgecolor', ...
'none', 'facecolor', 'g' , 'facealpha' , 0.5 );
hold off
% shading interp
camlight
view(3)
axis image
axis tightcamlight lighting gouraud
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
zlabel( sprintf( 'z (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('%s (%s) at t = %f %s', ...
MCDS.continuum_variables(1).name , ...
MCDS.continuum_variables(1).units , ...
MCDS.metadata.current_time, ...
MCDS.metadata.time_units ) );
You can get more 3-D volumetric visualization ideas at Matlab’s website. This visualization post at MIT also has some great tips.
Plotting the cells
Here is a basic 3-D plot for the cells:
plot3( MCDS.discrete_cells.state.position(:,1) , ...
MCDS.discrete_cells.state.position(:,2) , ...
MCDS.discrete_cells.state.position(:,3) , 'bo' );
view(3)
axis tight
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
zlabel( sprintf( 'z (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('Cells at t = %f %s', MCDS.metadata.current_time, ...
MCDS.metadata.time_units ) );
plot3 is more efficient than scatter3, but scatter3 will give more coloring options. Here is the syntax:
scatter3( MCDS.discrete_cells.state.position(:,1), ...
MCDS.discrete_cells.state.position(:,2), ...
MCDS.discrete_cells.state.position(:,3) , 'bo' );
view(3)
axis tight
xlabel( sprintf( 'x (%s)' , MCDS.metadata.spatial_units) );
ylabel( sprintf( 'y (%s)' , MCDS.metadata.spatial_units) );
zlabel( sprintf( 'z (%s)' , MCDS.metadata.spatial_units) );
title( sprintf('Cells at t = %f %s', MCDS.metadata.current_time, ...
MCDS.metadata.time_units ) );
Jan Poleszczuk gives some great insights on plotting many cells in 3D at his blog. I’d recommend checking out his post on visualizing a cellular automaton model. At some point, I’ll update this post with prettier plotting based on his methods.
What’s next
Future releases of BioFVM will support reading MultiCellDS snapshots (for model initialization).
Matlab is pretty slow at parsing and visualizing large amounts of data. We also plan to include resources for accessing MultiCellDS data in VTK / Paraview and Python.
Return to News • Return to MathCancer • Follow @MathCancer