Category: publication
A small computational thought experiment
In Macklin (2017), I briefly touched on a simple computational thought experiment that shows that for a group of homogeneous cells, you can observe substantial heterogeneity in cell behavior. This “thought experiment” is part of a broader preview and discussion of a fantastic paper by Linus Schumacher, Ruth Baker, and Philip Maini published in Cell Systems, where they showed that a migrating collective homogeneous cells can show heterogeneous behavior when quantitated with new migration metrics. I highly encourage you to check out their work!
In this blog post, we work through my simple thought experiment in a little more detail.
Note: If you want to reference this blog post, please cite the Cell Systems preview article:
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
The thought experiment
Consider a simple (and widespread) model of a population of cycling cells: each virtual cell (with index i) has a single “oncogene” \( r_i \) that sets the rate of progression through the cycle. Between now (t) and a small time from now ( \(t+\Delta t\)), the virtual cell has a probability \(r_i \Delta t\) of dividing into two daughter cells. At the population scale, the overall population growth model that emerges from this simple single-cell model is:
\[\frac{dN}{dt} = \langle r\rangle N, \]
where \( \langle r \rangle \) the mean division rate over the cell population, and N is the number of cells. See the discussion in the supplementary information for Macklin et al. (2012).
Now, suppose (as our thought experiment) that we could track individual cells in the population and track how long it takes them to divide. (We’ll call this the division time.) What would the distribution of cell division times look like, and how would it vary with the distribution of the single-cell rates \(r_i\)?
Mathematical method
In the Matlab script below, we implement this cell cycle model as just about every discrete model does. Here’s the pseudocode:
t = 0;
while( t < t_max )
for i=1:Cells.size()
u = random_number();
if( u < Cells[i].birth_rate * dt )
Cells[i].division_time = Cells[i].age;
Cells[i].divide();
end
end
t = t+dt;
end
That is, until we’ve reached the final simulation time, loop through all the cells and decide if they should divide: For each cell, choose a random number between 0 and 1, and if it’s smaller than the cell’s division probability (\(r_i \Delta t\)), then divide the cell and write down the division time.
As an important note, we have to track the same cells until they all divide, rather than merely record which cells have divided up to the end of the simulation. Otherwise, we end up with an observational bias that throws off our recording. See more below.
The sample code
You can download the Matlab code for this example at:
http://MathCancer.org/files/matlab/thought_experiment_matlab(Macklin_Cell_Systems_2017).zip
Extract all the files, and run “thought_experiment” in Matlab (or Octave, if you don’t have a Matlab license or prefer an open source platform) for the main result.
All these Matlab files are available as open source, under the GPL license (version 3 or later).
Results and discussion
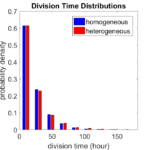
First, let’s see what happens if all the cells are identical, with \(r = 0.05 \textrm{ hr}^{-1}\). We run the script, and track the time for each of 10,000 cells to divide. As expected by theory (Macklin et al., 2012) (but perhaps still a surprise if you haven’t looked), we get an exponential distribution of division times, with mean time \(1/\langle r \rangle\):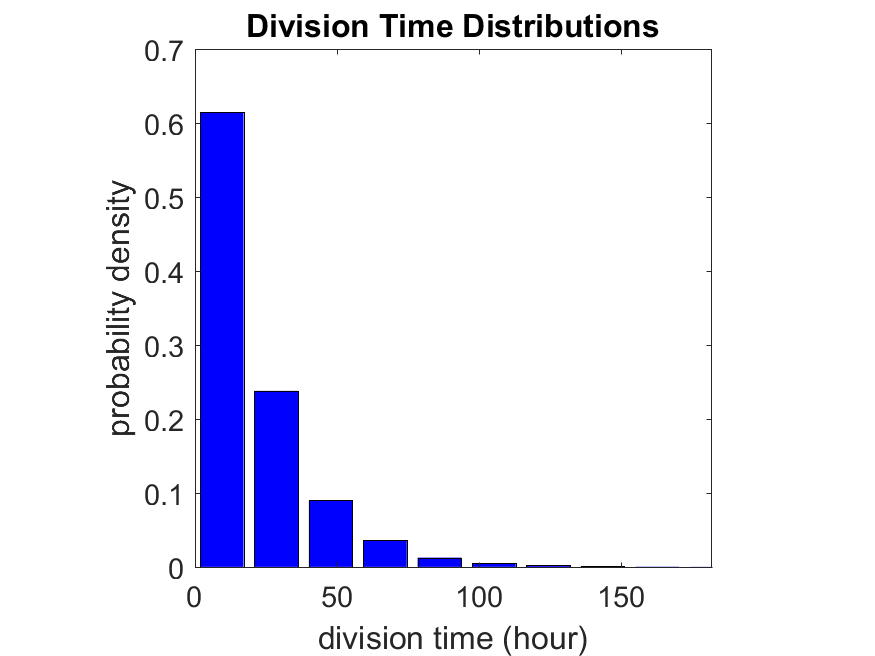
So even in this simple model, a homogeneous population of cells can show heterogeneity in their behavior. Here’s the interesting thing: let’s now give each cell its own division parameter \(r_i\) from a normal distribution with mean \(0.05 \textrm{ hr}^{-1}\) and a relative standard deviation of 25%: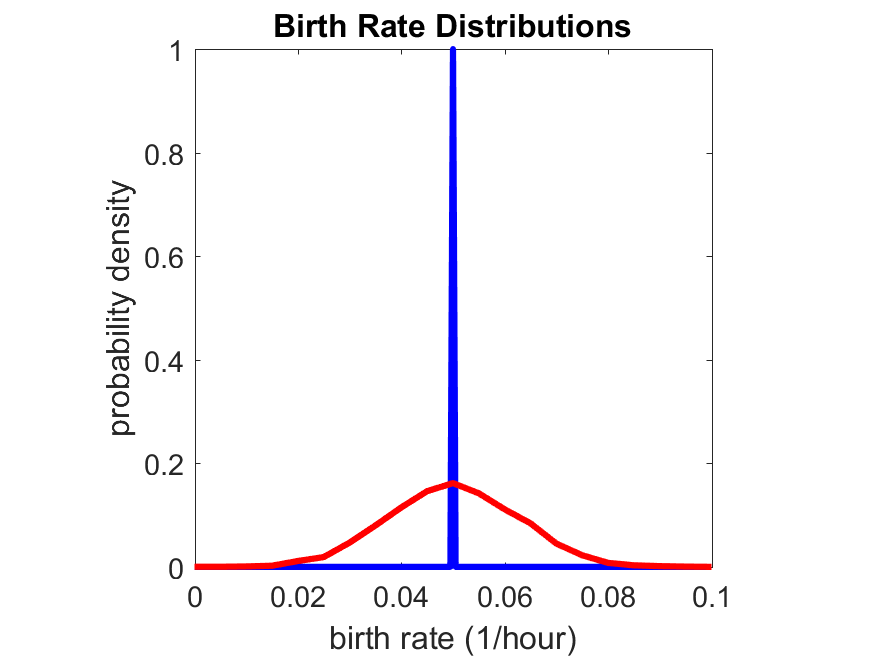
If we repeat the experiment, we get the same distribution of cell division times!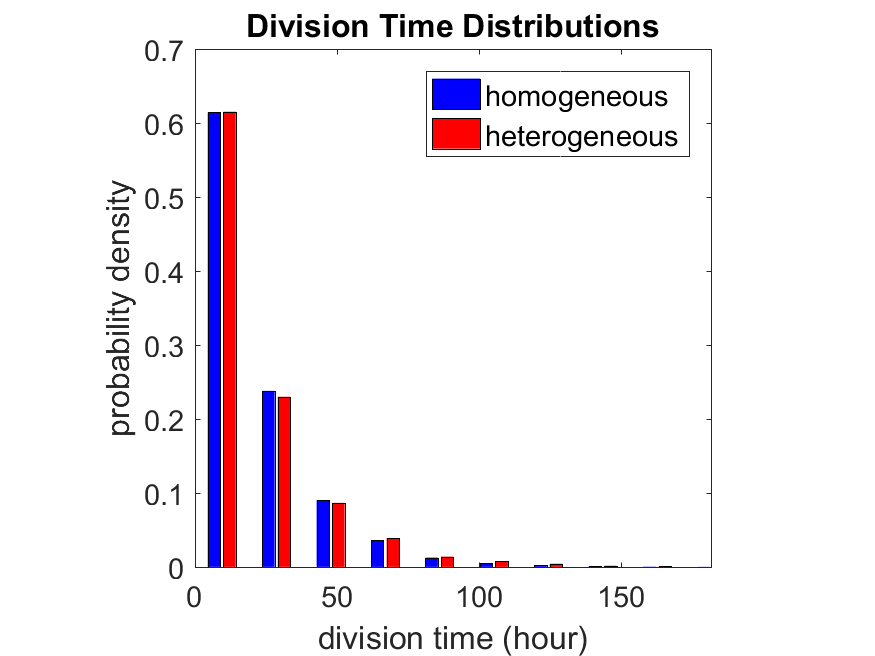
So in this case, based solely on observations of the phenotypic heterogeneity (the division times), it is impossible to distinguish a “genetically” homogeneous cell population (one with identical parameters) from a truly heterogeneous population. We would require other metrics, like tracking changes in the mean division time as cells with a higher \(r_i\) out-compete the cells with lower \(r_i\).
Lastly, I want to point out that caution is required when designing these metrics and single-cell tracking. If instead we had tracked all cells throughout the simulated experiment, including new daughter cells, and then recorded the first 10,000 cell division events, we would get a very different distribution of cell division times: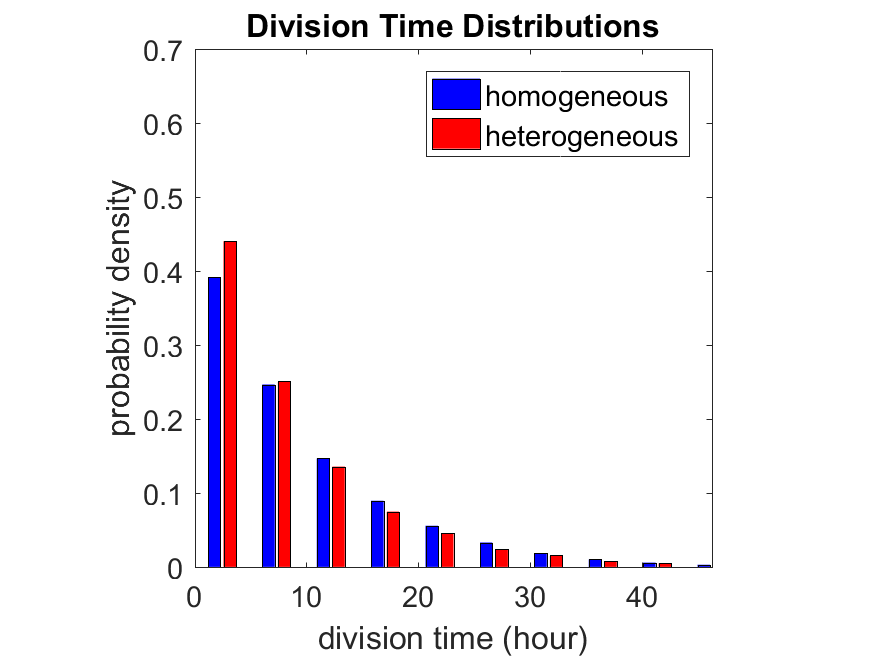
By only recording the division times for the cells that have divided, and not those that haven’t, we bias our observations towards cells with shorter division times. Indeed, the mean division time for this simulated experiment is far lower than we would expect by theory. You can try this one by running “bad_thought_experiment”.
Further reading
This post is an expansion of our recent preview in Cell Systems in Macklin (2017):
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
And the original work on apparent heterogeneity in collective cell migration is by Schumacher et al. (2017):
L. Schumacher et al., Semblance of Heterogeneity in Collective Cell Migration. Cell Sys., 2017 (in press). DOI: 10.1016/j.cels.2017.06.006
You can read some more on relating exponential distributions and Poisson processes to common discrete mathematical models of cell populations in Macklin et al. (2012):
P. Macklin, et al., Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 301:122-40, 2012. DOI: 10.1016/j.jtbi.2012.02.002.
Lastly, I’d be delighted if you took a look at the open source software we have been developing for 3-D simulations of multicellular systems biology:
http://OpenSource.MathCancer.org
And you can always keep up-to-date by following us on Twitter: @MathCancer.
DCIS modeling paper accepted
I am pleased to report that our paper has now been accepted. You can download the accepted preprint here. We also have a lot of supplementary material, including simulation movies, simulation datasets (for 0, 15, 30, adn 45 days of growth), and open source C++ code for postprocessing and visualization.
I discussed the results in detail here, but here’s the short version:
- We use a mechanistic, agent-based model of individual cancer cells growing in a duct. Cells are moved by adhesive and repulsive forces exchanged with other cells and the basement membrane. Cell phenotype is controlled by stochastic processes.
- We constrained all parameter expected to be relatively independent of patients by a careful analysis of the experimental biological and clinical literature.
- We developed the very first patient-specific calibration method, using clinically-accessible pathology. This is a key point in future patient-tailored predictions and surgical/therapeutic planning.
- The model made numerous quantitative predictions, such as:
- The tumor grows at a constant rate, between 7 to 10 mm/year. This is right in the middle of the range reported in the clinic.
- The tumor’s size in mammgraphy is linearly correlated with the post-surgical pathology size. When we linearly extrapolate our correlation across two orders of magnitude, it goes right through the middle of a cluster of 87 clinical data points.
- The tumor necrotic core has an age structuring: with oldest, calcified material in the center, and newest, most intact necrotic cells at the outer edge.
- The appearance of a “typical” DCIS duct cross-section varies with distance from the leading edge; all types of cross-sections predicted by our model are observed in patient pathology.
- The model also gave new insight on the underlying biology of breast cancer, such as:
- The split between the viable rim and necrotic core (observed almost universally in pathology) is not just an artifact, but an actual biomechanical effect from fast necrotic cell lysis.
- The constant rate of tumor growth arises from the biomechanical stress relief provided by lysing necrotic cells. This points to the critical role of intracellular and intra-tumoral water transport in determining the qualitative and quantitative behavior of tumors.
- Pyknosis (nuclear degradation in necrotic cells), must occur at a time scale between that of cell lysis (on the order of hours) and cell calcification (on the order of weeks).
- The current model cannot explain the full spectrum of calcification types; other biophysics, such as degradation over a long, 1-2 month time scale, must be at play.
DCIS paper resubmitted; lots of clinical predictions, lots of validation
After a lot of revision, I have merged my two papers on ductal carcinoma in situ (DCIS) in to a single manuscript and resubmitted to the Journal of Theoretical Biology for final review. A preprint is posted at my website, along with considerable supplementary material (data sets and source code, and animations). Thanks to my co-authors and other friends for all the help in the revisions. Thanks also the reviewers for insightful comments. I think this revised manuscript is all the better for it.
DCIS is a precursor to invasive breast cancer, and it is generally detected by annual mammographic screening. More advanced DCIS (with greater risk) tends to have comedonecrosis–a type of cell death that leaves calcium phosphate deposits in the centers of the ducts. In fact, this is generally what’s detected in mammograms. DCIS is usually surgically removed by cutting out a small ball of tissue around what’s found in the mammograms (breast-conserving surgery, or lumpectomy). But current planning isn’t so great. Even with the state-of-the-art in patient imaging and surgical planning, about 20%-50% of women need to get a second surgery because the first one didn’t get the entire tumor.
So, there’s great need to understand calcifications, and how what you see in mammography relates to the actual tumor size and shape. And if you do have a model to do this, there’s great need to calibrate it to patient pathology data (the stuff you get from your biopsies) so that the models say something meaningful about individual patients. And there has been no method to do that. Until now.
(As far as I know), this paper is the first to calibrate to individual patient immunohistochemistry and histopathology. This, along with some parameter estimates to the theoretical and experimental biology literature, allows us to fully constrain the model. No free parameters to play with until it looks right. Any results are fully emergent from a mechanistic model and realistic parameter estimates rooted in the biology.
This model also includes the most detailed description of necrosis–the type of cell death that results in the comedonecrosis seen in mammograms. We include cell swelling, cell bursting, gradual loss of fluid, and the very first model of calcification.
Clinical predictions, with lots of validation:
All said and done, the model gives some big (and validated!) predictions:
- The model predicts that a tumor grows through the duct at a constant rate. This is consistent with what’s actually seen in mammography.
- The model gives a new explanation for the known trend: when necrotic cells burst and lose fluid, it makes it more mechanically favorable for proliferating cells to push into the center of the duct, rather than along the duct. For this reason the model predicts faster growth in smaller ducts, and slower growth in larger ducts.
- The model predicts growth rates between 7.5 and 10 mm per year. This is quantitatively consistent with published values in the clinical literature.
- The model predicts the difference between the size in a mammogram and the actual size (as measured by a pathologist after surgery) grows in time. This unfortunately means that it’s unlikely that there is some “fixed” safe distance to cut around the mammographic findings.
- On the other hand, the model predicts that there is a linear correlation between the size in a mammogram and the actual (pathology) tumor size. This bodes well for future surgical planning.
- Better still, the linear correlation we found quantitatively fits through 87 published patients, spanning two orders of magnitude.
The model also makes several key predictions on the smaller-scale biology:
- The model predicts that fast swelling of necrotic cells (on the order of 6 hours) is responsible for the tear between the viable rim and necrotic core seen in just about every pathology image of DCIS.
- The model predicts that the necrotic core is “age structured”, with newly necrotic cells (with relatively intact nuclei) on the outer edge, and interior band of mostly degraded but noncalcified cells, and a central core of oldest, calcified material. This compares well with patient histopathology.
- Comparing the model-predicted age structuring to histopathology predicts a sharper estimate on the various necrosis time scales: swelling and lysis (~6 h) < slow fluid loss (~days to a week) < pyknosis (~10+ days) < calcification (~2 weeks).
- Because the model only predicts linear / casting-type calcifications (long “plugs” of calcification), other biophysics must be responsible for the variety of calcification types seen in mammography.
- Among other mechanisms, we postulate a very long-timescale (1-2 months) process of degradation of the phospholipid “backbone” of the calcifications, resulting in degradation of the calcifications. The cracks seen in the central portions of calcifications (in histopathology) supports this view.