Category: open source
Introducing cell interactions & transformations
Introduction
PhysiCell 1.10.0 introduces a number of new features designed to simplify modeling of complex interactions and transformations. This blog post will introduce the underlying mathematics and show a complete example. We will teach this and other examples in greater depth at our upcoming Virtual PhysiCell Workshop & Hackathon (July 24-30, 2022). (Apply here!!)
Cell Interactions
In the past, it has been possible to model complex cell-cell interactions (such as those needed for microecology and immunology) by connecting basic cell functions for interaction testing and custom functions. In particular, these functions were used for the COVID19 Coalition’s open source model of SARS-CoV-2 infections and immune responses. We now build upon that work to standardize and simplify these processes, making use of the cell’s state.neighbors (a list of all cells deemed to be within mechanical interaction distance).
All the parameters for cell-cell interactions are stored in cell.phenotype.cell_interactions.
Phagocytosis
A cell can phagocytose (ingest) another cell, with rates that vary with the cell’s live/dead status or the cell type. In particular, we store:
- double dead_phagocytosis_rate : This is the rate at which a cell can phagocytose a dead cell of any type.
std::vector<double> live_phagocytosis_rates: This is a vector of phagocytosis rates for live cells of specific types. If there are n cell definitions in the simulation, then there are n rates in this vector. Please note that the index i for any cell type is its index in the list of cell definitions, not necessarily the ID of its cell definition. For safety, use one of the following to determine that index:find_cell_definition_index( int type_ID ): search for the cell definition’s index by its type ID (cell.type)find_cell_definition_index( std::string type_name ): search for the cell definition’s index by its human-readable type name (cell.type_name)
We also supply a function to help access these live phagocytosis rates.
- double& live_phagocytosis_rate( std::string type_name ) : Directly access the cell’s rate of phagocytosing the live cell type by its human-readable name. For example,
pCell->phenotype.cell_interactions.live_phagocytosis_rate( "tumor cell" ) = 0.01;
At each mechanics time step (with duration \(\Delta t\), default 0.1 minutes), each cell runs through its list of neighbors. If the neighbor is dead, its probability of phagocytosing it between \(t\) and \(t+\Delta t\) is
\[ \verb+dead_phagocytosis_rate+ \cdot \Delta t\]
If the neighbor cell is alive and its type has index j, then its probability of phagocytosing the cell between \(t\) and \(t+\Delta t\) is
\[ \verb+live_phagocytosis_rates[j]+ \cdot \Delta t\]
PhysiCell’s standardized phagocytosis model does the following:
- The phagocytosing cell will absorb the phagocytosed cell’s total solid volume into the cytoplasmic solid volume
- The phagocytosing cell will absorb the phagocytosed cell’s total fluid volume into the fluid volume
- The phagocytosing cell will absorb all of the phagocytosed cell’s internalized substrates.
- The phagocytosed cell is set to zero volume, flagged for removal, and set to not mechanically interact with remaining cells.
- The phagocytosing cell does not change its target volume. The standard volume model will gradually “digest” the absorbed volume as the cell shrinks towards its target volume.
Cell Attack
A cell can attack (cause damage to) another live cell, with rates that vary with the cell’s type. In particular, we store:
- double damage_rate : This is the rate at which a cell causes (dimensionless) damage to a target cell. The cell’s total damage is stored in cell.state.damage. The total integrated attack time is stored in
cell.state.total_attack_time. std::vector<double> attack_rates: This is a vector of attack rates for live cells of specific types. If there are n cell definitions in the simulation, then there are n rates in this vector. Please note that the index i for any cell type is its index in the list of cell definitions, not necessarily the ID of its cell definition. For safety, use one of the following to determine that index:find_cell_definition_index( int type_ID ): search for the cell definition’s index by its type ID (cell.type)find_cell_definition_index( std::string type_name ): search for the cell definition’s index by its human-readable type name (cell.type_name)
We also supply a function to help access these attack rates.
- double& attack_rate( std::string type_name ) : Directly access the cell’s rate of attacking the live cell type by its human-readable name. For example,
pCell->phenotype.cell_interactions.attack_rate( "tumor cell" ) = 0.01;
At each mechanics time step (with duration \(\Delta t\), default 0.1 minutes), each cell runs through its list of neighbors. If the neighbor cell is alive and its type has index j, then its probability of attacking the cell between \(t\) and \(t+\Delta t\) is
\[ \verb+attack_rates[j]+ \cdot \Delta t\]
To attack the cell:
- The attacking cell will increase the target cell’s damage by \( \verb+damage_rate+ \cdot \Delta t\).
- The attacking cell will increase the target cell’s total attack time by \(\Delta t\).
Note that this allows us to have variable rates of damage (e.g., some immune cells may be “worn out”), and it allows us to distinguish between damage and integrated interaction time. (For example, you may want to write a model where damage can be repaired over time.)
As of this time, PhysiCell does not have a standardized model of death in response to damage. It is up to the modeler to vary a death rate with the total attack time or integrated damage, based on their hypotheses. For example:
\[ r_\textrm{apoptosis} = r_\textrm{apoptosis,0} + \left( r_\textrm{apoptosis,max} – r_\textrm{apoptosis,0} \right) \cdot \frac{ d^h }{ d_\textrm{halfmax}^h + d^h } \]
In a phenotype function, we might write this as:
void damage_response( Cell* pCell, Phenotype& phenotype, double dt )
{ // get the base apoptosis rate from our cell definition
Cell_Definition* pCD = find_cell_definition( pCell->type_name );
double apoptosis_0 = pCD->phenotype.death.rates[0];
double apoptosis_max = 100 * apoptosis_0;
double half_max = 2.0;
double damage = pCell->state.damage;
phenotype.death.rates[0] = apoptosis_0 +
(apoptosis_max -apoptosis_0) * Hill_response_function(d,half_max,1.0);
return;
}
Cell Fusion
A cell can fuse with another live cell, with rates that vary with the cell’s type. In particular, we store:
std::vector<double> fusion_rates: This is a vector of fusion rates for live cells of specific types. If there are n cell definitions in the simulation, then there are n rates in this vector. Please note that the index i for any cell type is its index in the list of cell definitions, not necessarily the ID of its cell definition. For safety, use one of the following to determine that index:find_cell_definition_index( int type_ID ): search for the cell definition’s index by its type ID (cell.type)find_cell_definition_index( std::string type_name ): search for the cell definition’s index by its human-readable type name (cell.type_name)
We also supply a function to help access these fusion rates.
- double& fusion_rate( std::string type_name ) : Directly access the cell’s rate of fusing with the live cell type by its human-readable name. For example,
pCell->phenotype.cell_interactions.fusion_rate( "tumor cell" ) = 0.01;
At each mechanics time step (with duration \(\Delta t\), default 0.1 minutes), each cell runs through its list of neighbors. If the neighbor cell is alive and its type has index j, then its probability of fusing with the cell between \(t\) and \(t+\Delta t\) is
\[ \verb+fusion_rates[j]+ \cdot \Delta t\]
PhysiCell’s standardized fusion model does the following:
- The fusing cell will absorb the fused cell’s total cytoplasmic solid volume into the cytoplasmic solid volume
- The fusing cell will absorb the fused cell’s total nuclear volume into the nuclear solid volume
- The fusing cell will keep track of its number of nuclei in
state.number_of_nuclei. (So, if the fusing cell has 3 nuclei and the fused cell has 2 nuclei, then the new cell will have 5 nuclei.) - The fusing cell will absorb the fused cell’s total fluid volume into the fluid volume
- The fusing cell will absorb all of the fused cell’s internalized substrates.
- The fused cell is set to zero volume, flagged for removal, and set to not mechanically interact with remaining cells.
- The fused cell will be moved to the (volume weighted) center of mass of the two original cells.
- The fused cell does change its target volume to the sum of the original two cells’ target volumes. The combined cell will grow / shrink towards its new target volume.
Cell Transformations
A live cell can transform to another type (e.g., via differentiation). We store parameters for cell transformations in cell.phenotype.cell_transformations, particularly:
std::vector<double> transformation_rates: This is a vector of transformation rates from a cell’s current to type to one of the other cell types. If there are n cell definitions in the simulation, then there are n rates in this vector. Please note that the index i for any cell type is its index in the list of cell definitions, not necessarily the ID of its cell definition. For safety, use one of the following to determine that index:find_cell_definition_index( int type_ID ): search for the cell definition’s index by its type ID (cell.type)find_cell_definition_index( std::string type_name ): search for the cell definition’s index by its human-readable type name (cell.type_name)
We also supply a function to help access these transformation rates.
- double& transformation_rate( std::string type_name ) : Directly access the cell’s rate of transforming into a specific cell type by searching for its human-readable name. For example,
pCell->phenotype.cell_transformations.transformation_rate( "mutant tumor cell" ) = 0.01;
At each phenotype time step (with duration \(\Delta t\), default 6 minutes), each cell runs through the vector of transformation rates. If a (different) cell type has index j, then the cell’s probability transforming to that type between \(t\) and \(t+\Delta t\) is
\[ \verb+transformation_rates[j]+ \cdot \Delta t\]
PhysiCell uses the built-in Cell::convert_to_cell_definition( Cell_Definition& ) for the transformation.
Other New Features
This release also includes a number of handy new features:
Advanced Chemotaxis
After setting chemotaxis sensitivities in phenotype.motility and enabling the feature, cells can chemotax based on linear combinations of substrate gradients.
std::vector<double> phenotype.motility.chemotactic_sensitivitiesis a vector of chemotactic sensitivities, one for each substrate in the environment. By default, these are all zero for backwards compatibility. A positive sensitivity denotes chemotaxis up a corresponding substrate’s gradient (towards higher values), whereas a negative sensitivity gives chemotaxis against a gradient (towards lower values).- For convenience, you can access (read and write) a substrate’s chemotactic sensitivity via
phenotype.motility.chemotactic_sensitivity(name)wherenameis the human-readable name of a substrate in the simulation. - If the user sets
cell.cell_functions.update_migration_bias = advanced_chemotaxis_function, then these sensitivities are used to set the migration bias direction via: \[\vec{d}_\textrm{mot} = s_0 \nabla \rho_0 + \cdots + s_n \nabla \rho_n. \] - If the user sets
cell.cell_functions.update_migration_bias = advanced_chemotaxis_function_normalized, then these sensitivities are used to set the migration bias direction via: \[\vec{d}_\textrm{mot} = s_0 \frac{\nabla\rho_0}{|\nabla\rho_0|} + \cdots + s_n \frac{ \nabla \rho_n }{|\nabla\rho_n|}.\]
Cell Adhesion Affinities
cell.phenotype.mechanics.adhesion_affinitiesis a vector of adhesive affinities, one for each cell type in the simulation. By default, these are all one for backwards compatibility.- For convenience, you can access (read and write) a cell’s adhesive affinity for a specific cell type via
phenotype.mechanics.adhesive_affinity(name), wherenameis the human-readable name of a cell type in the simulation. - The standard mechanics function (based on potentials) uses this as follows. If cell
ihas an cell-cell adhesion strengtha_iand an adhesive affinityp_ijto cell typej, and if celljhas a cell-cell adhesion strength ofa_jand an adhesive affinityp_jito cell typei, then the strength of their adhesion is \[ \sqrt{ a_i p_{ij} \cdot a_j p_{ji} }.\] Notice that if \(a_i = a_j\) and \(p_{ij} = p_{ji}\), then this reduces to \(a_i a_{pj}\). - The standard elastic spring function (
standard_elastic_contact_function) uses this as follows. If cellihas an elastic constanta_iand an adhesive affinityp_ijto cell typej, and if celljhas an elastic constanta_jand an adhesive affinityp_jito cell typei, then the strength of their adhesion is \[ \sqrt{ a_i p_{ij} \cdot a_j p_{ji} }.\] Notice that if \(a_i = a_j\) and \(p_{ij} = p_{ji}\), then this reduces to \(a_i a_{pj}\).
Signal and Behavior Dictionaries
We will talk about this in the next blog post. See http://www.mathcancer.org/blog/introducing-cell-signal-and-behavior-dictionaries.
A brief immunology example
We will illustrate the major new functions with a simplified cancer-immune model, where tumor cells attract macrophages, which in turn attract effector T cells to damage and kill tumor cells. A mutation process will transform WT cancer cells into mutant cells that can better evade this immune response.
The problem:
We will build a simplified cancer-immune system to illustrate the new behaviors.
- WT cancer cells: Proliferate and release a signal that will stimulate an immune response. Cancer cells can transform into mutant cancer cells. Dead cells release debris. Damage increases apoptotic cell death.
- Mutant cancer cells: Proliferate but release less of the signal, as a model of immune evasion. Dead cells release debris. Damage increases apoptotic cell death.
- Macrophages: Chemotax towards the tumor signal and debris, and release a pro-inflammatory signal. They phagocytose dead cells.
- CD8+ T cells: Chemotax towards the pro-inflammatory signal and cause damage to tumor cells. As a model of immune evasion, CD8+ T cells can damage WT cancer cells faster than mutant cancer cells.
We will use the following diffusing factors:
- Tumor signal: Released by WT and mutant cells at different rates. We’ll fix a 1 min\(^{-1}\) decay rate and set the diffusion parameter to 10000 \(\mu m^2/\)min to give a 100 micron diffusion length scale.
- Pro-inflammatory signal: Released by macrophages. We’ll fix a 1 min\(^{-1}\) decay rate and set the diffusion parameter to 10000 \(\mu;m^2/\)min to give a 100 micron diffusion length scale.
- Debris: Released by dead cells. We’ll fix a 0.01 min\(^{-1}\) decay rate and choose a diffusion coefficient of 1 \(\mu;m^2/\)min for a 10 micron diffusion length scale.
In particular, we won’t worry about oxygen or resources in this model. We can use Neumann (no flux) boundary conditions.
Getting started with a template project and the graphical model builder
The PhysiCell Model Builder was developed by Randy Heiland and undergraduate researchers at Indiana University to help ease the creation of PhysiCell models, with a focus on generating correct XML configuration files that define the diffusing substrates and cell definitions. Here, we assume that you have cloned (or downloaded) the repository adjacent to your PhysiCell repository. (So that the path to PMB from PhysiCell’s root directory is ../PhysiCell-model-builder/).
Let’s start a new project (starting with the template project) from a command prompt or shell in the PhysiCell directory, and then open the model builder.
make template make python ../PhysiCell-model-builder/bin/pmb.py
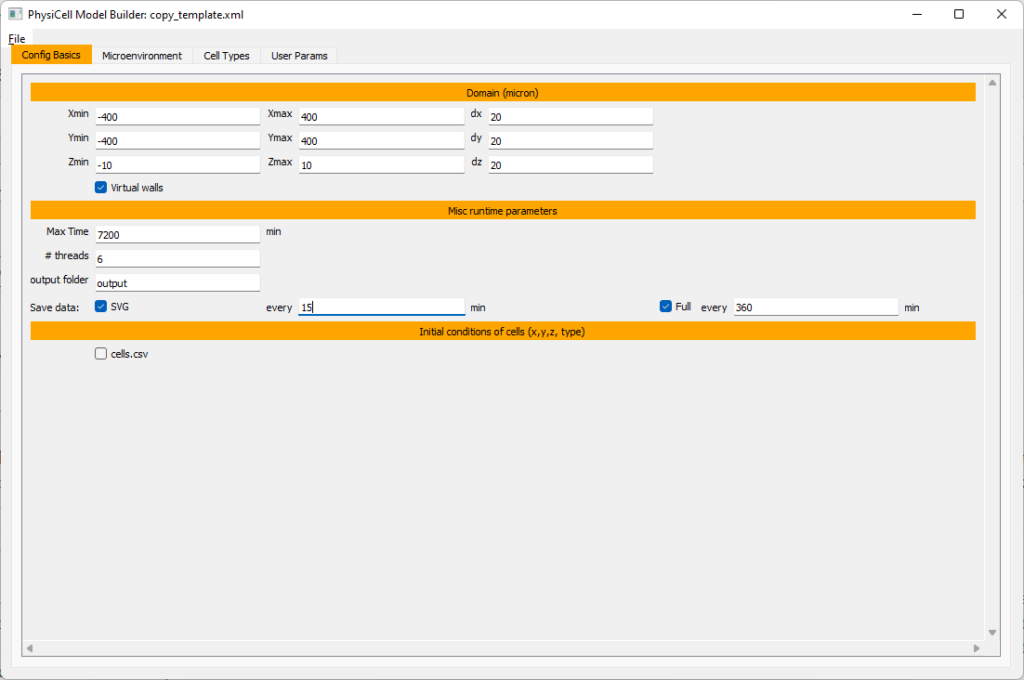
Setting up the domain
Let’s use a [-400,400] x [-400,400] 2D domain, with “virtual walls” enabled (so cells stay in the domain). We’ll run for 5760 minutes (4 days), saving SVG outputs every 15 minutes.
Setting up diffusing substrates
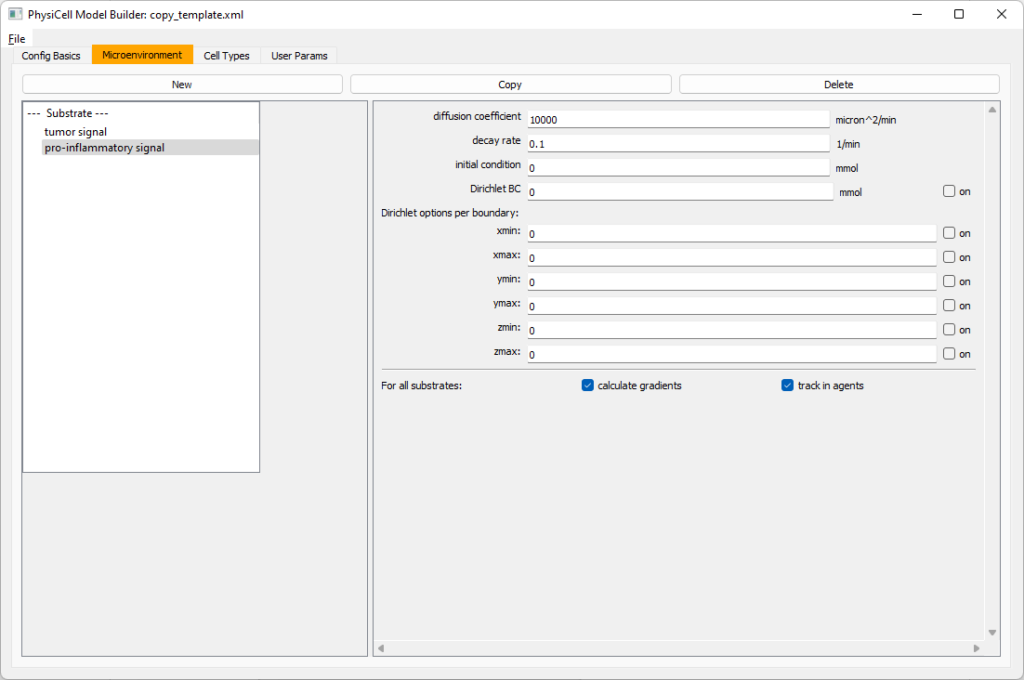
Move to the microenvironment tab. Click on substrate and rename it to tumor signal . Set the decay rate to 0.1 and diffusion parameter to 10000. Uncheck the Dirichlet condition box so that it’s a zero-flux (Neumann) boundary condition.
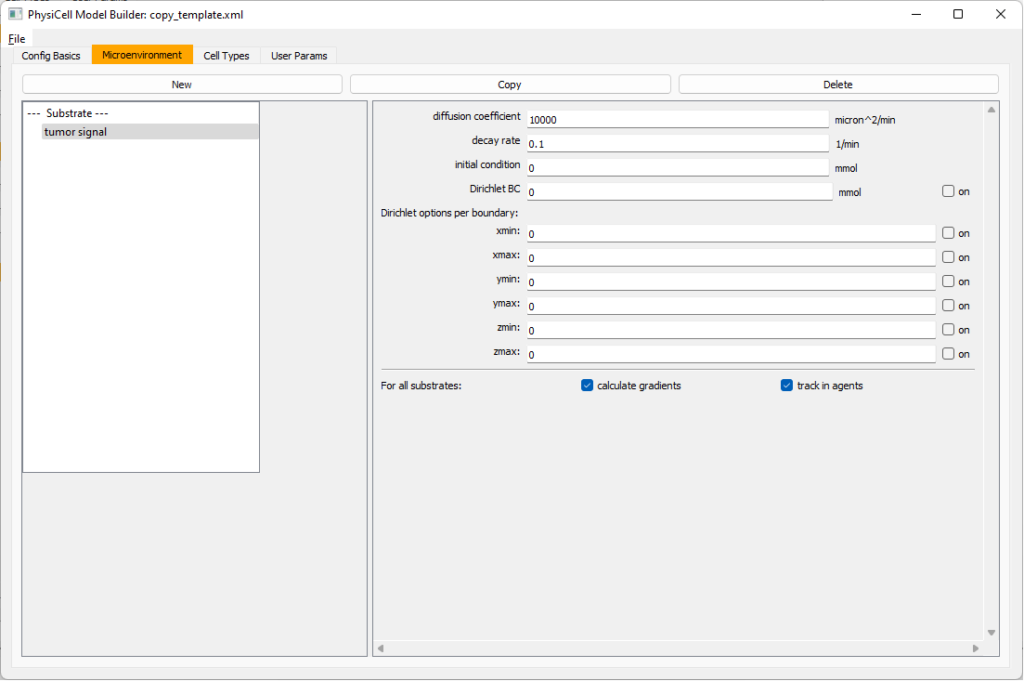 Now, select
Now, select tumor signal in the lefthand column, click copy, and rename the new substrate (substrate01) to pro-inflammatory signal with the same parameters.
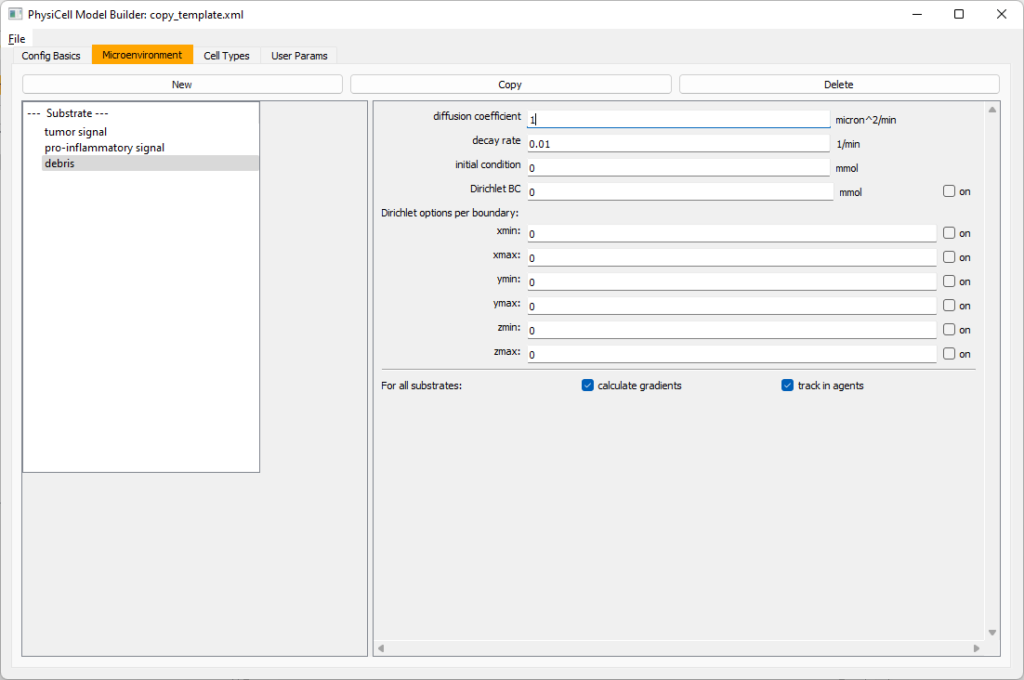
Then, copy this substrate one more time, and rename it from name debris. Set its decay rate to 0.01, and its diffusion parameter to 1.
Let’s save our work before continuing. Go to File, Save as, and save it as PhysiCell_settings.xml in your config file. (Go ahead and overwrite.)
If model builder crashes, you can reopen it, then go to File, Open, and select this file to continue editing.
Setting up the WT cancer cells
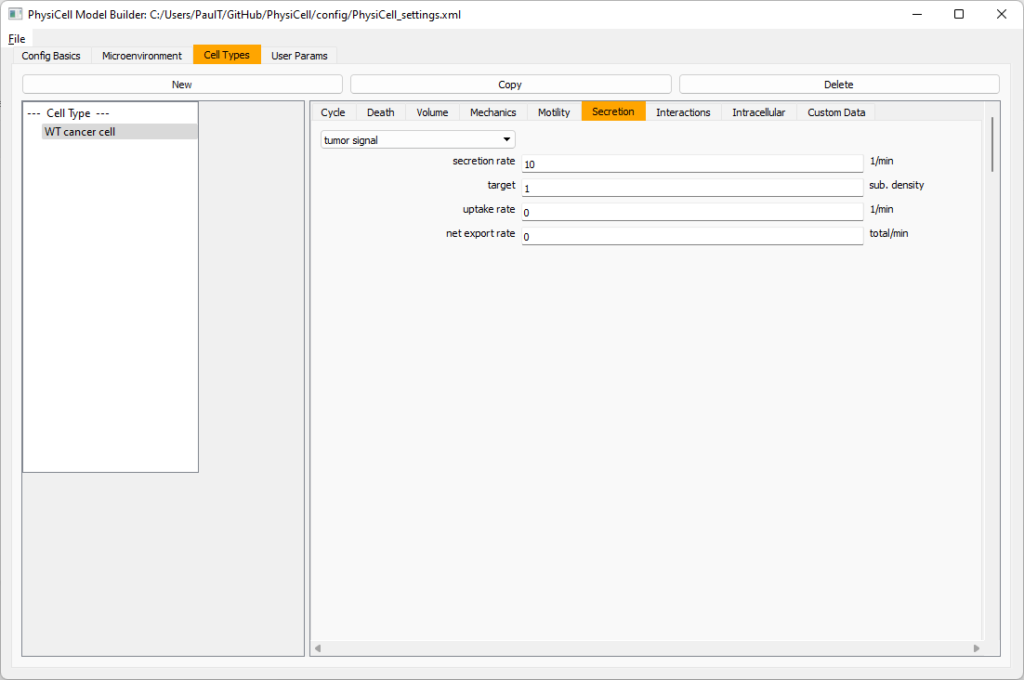
Move to the cell types tab. Click on the default cell type on the left side, and rename it to WT cancer cell. Leave most of the parameter values at their defaults. Move to the secretion sub-tab (in phenotype). From the drop-down menu, select tumor signal. Let’s set a high secretion rate of 10.
We’ll need to set WT cells as able to mutate, but before that, the model builder needs to “know” about that cell type. So, let’s move on to the next cell type for now.
Setting up mutant tumor cells
Click the WT cancer cell in the left column, and click copy. Rename this cell type (for me, it’s cell_def03) to mutant cancer cell. Click the secretion sub-tab, and set its secretion rate of tumor signal lower to 0.1.
Set the WT mutation rate
Now that both cell types are in the simulation, we can set up mutation. Let’s suppose the mean time to a mutation is 10000 minutes, or a rate of 0.0001 min\(^{-1}\).
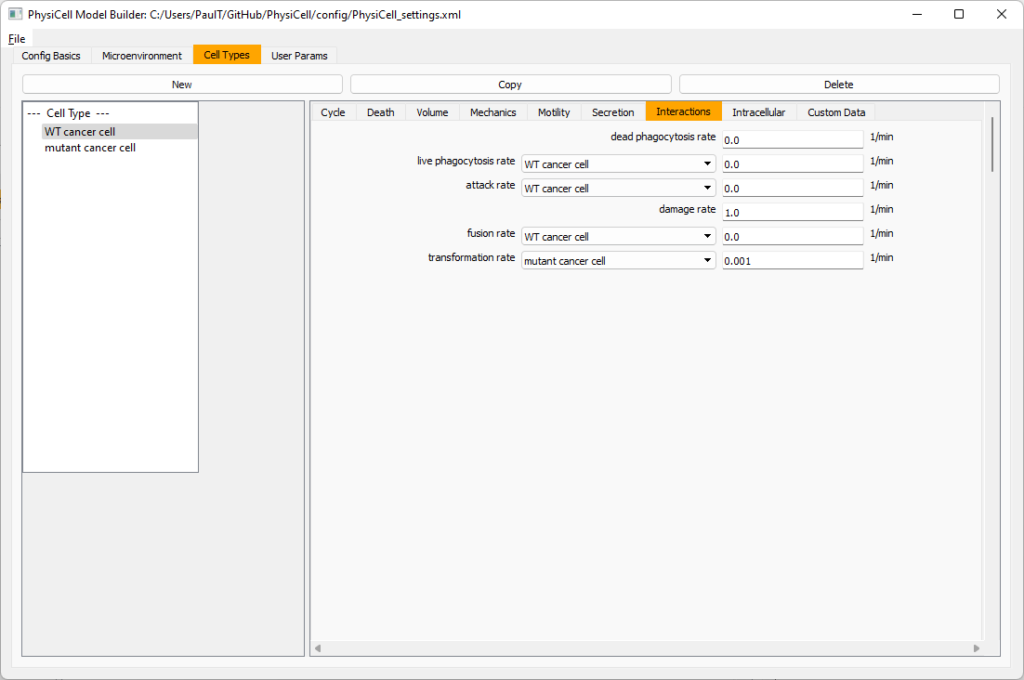
Click the WT cancer cell in the left column to select it. Go to the interactions tab. Go down to transformation rate, and choose mutant cancer cell from the drop-down menu. Set its rate to 0.0001.
Create macrophages
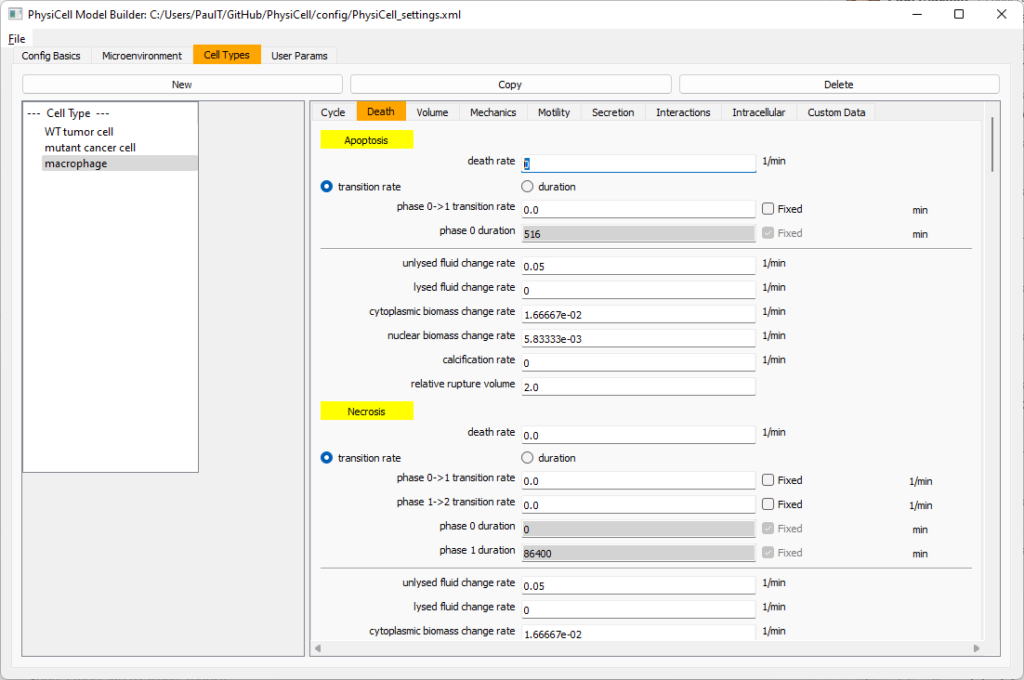
Now click on the WT cancer cell type in the left column, and click copy to create a new cell type. Click on the new type (for me cell_def04) and rename it to macrophage.
Click on cycle and change to a live cells and change from a duration representation to a transition rate representation. Keep its cycling rate at 0.
Go to death and change from duration to transition rate for both apoptosis and necrosis, and keep the death rates at 0.0
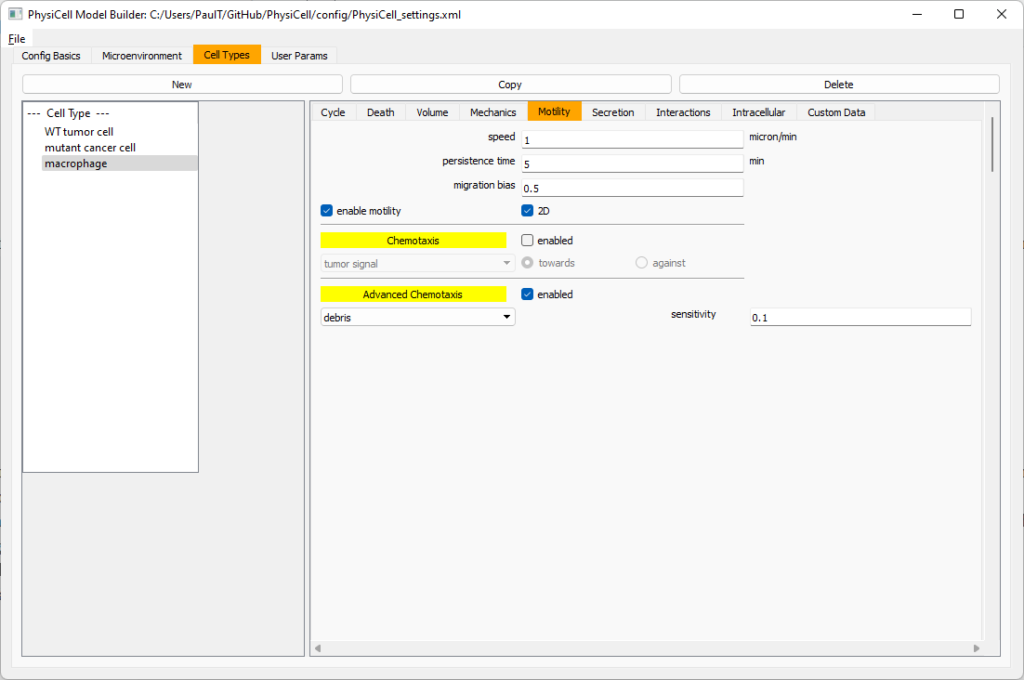
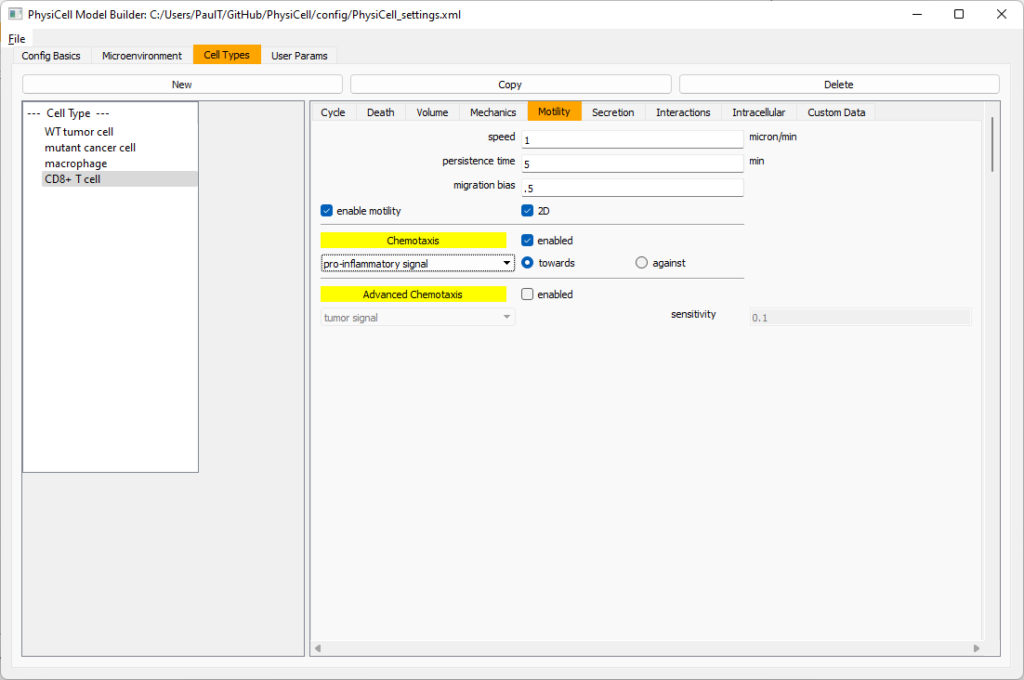
Now, go to the motility tab. Set the speed to 1 \(\mu m/\)min, persistence time to 5 min, and migration bias to 0.5. Be sure to enable motility. Then, enable advanced motility. Choose tumor signal from the drop-down and set its sensitivity to 1.0. Then choose debris from the drop-down and set its sensitivity to 0.1
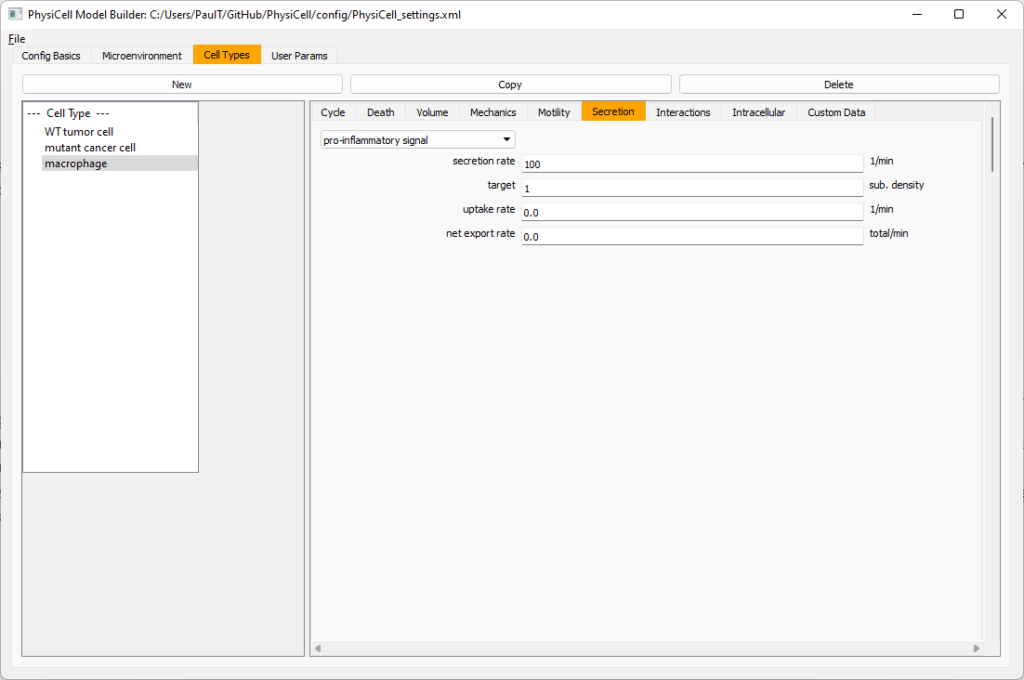
Now, let’s make sure it secretes pro-inflammatory signal. Go to the secretion tab. Choose tumor signal from the drop-down, and make sure its secretion rate is 0. Then choose pro-inflammatory signal from the drop-down, set its secretion rate to 100, and its target value to 1.
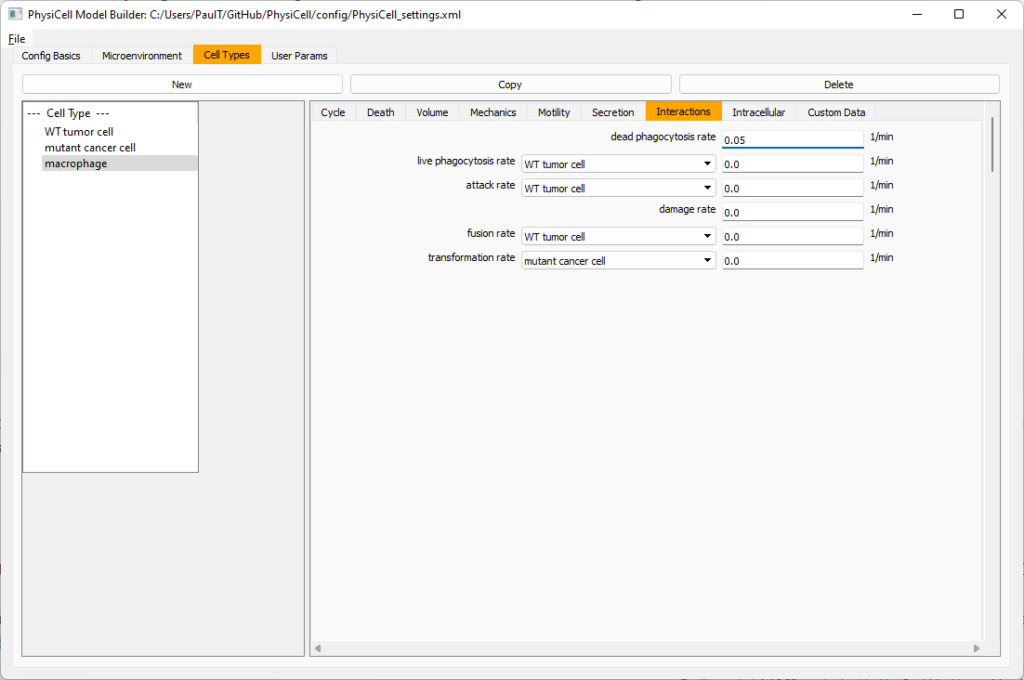
Lastly, let’s set macrophages up to phagocytose dead cells. Go to the interactions tab. Set the dead phagocytosis rate to 0.05 (so that the mean contact time to wait to eat a dead cell is 1/0.05 = 20 minutes). This would be a good time to save your work.
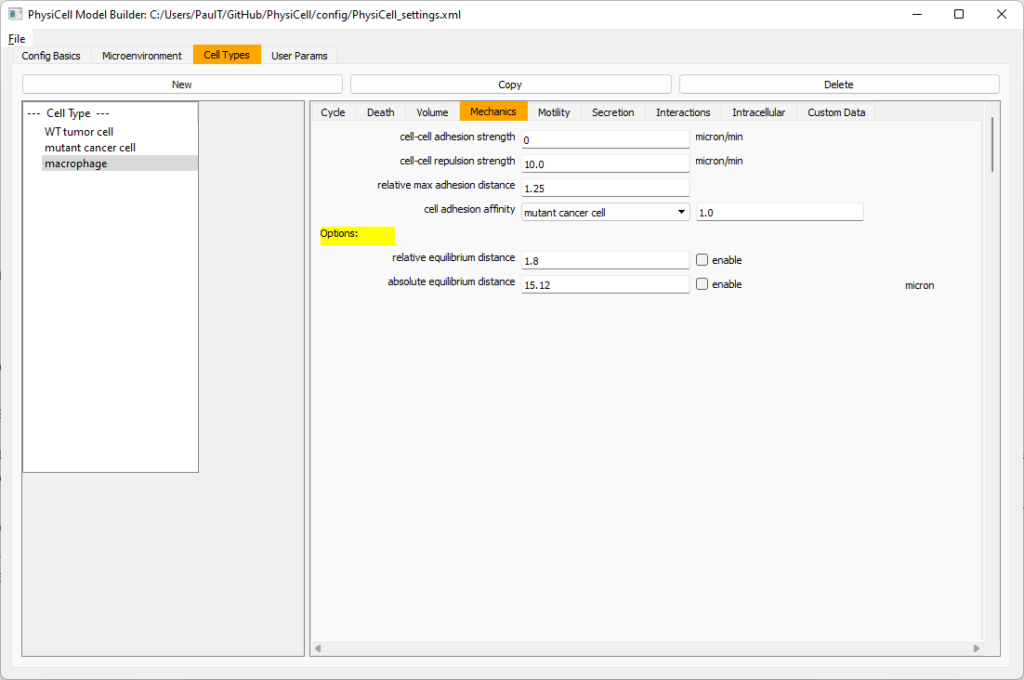
Macrophages probably shouldn’t be adhesive. So go to the mechanics sub-tab, and set the cell-cell adhesion strength to 0.0.
Create CD8+ T cells
Select macrophage on the left column, and choose copy. Rename the new cell type to CD8+ T cell. Go to the secretion sub-tab and make sure to set the secretion rate of pro-inflammatory signal to 0.0.
Now, let’s use simpler chemotaxis for these towards pro-inflammatory signal. Go to the motility tab. Uncheck advanced chemotaxis and check chemotaxis. Choose pro-inflammatory signal from the drop-down, with the towards option.
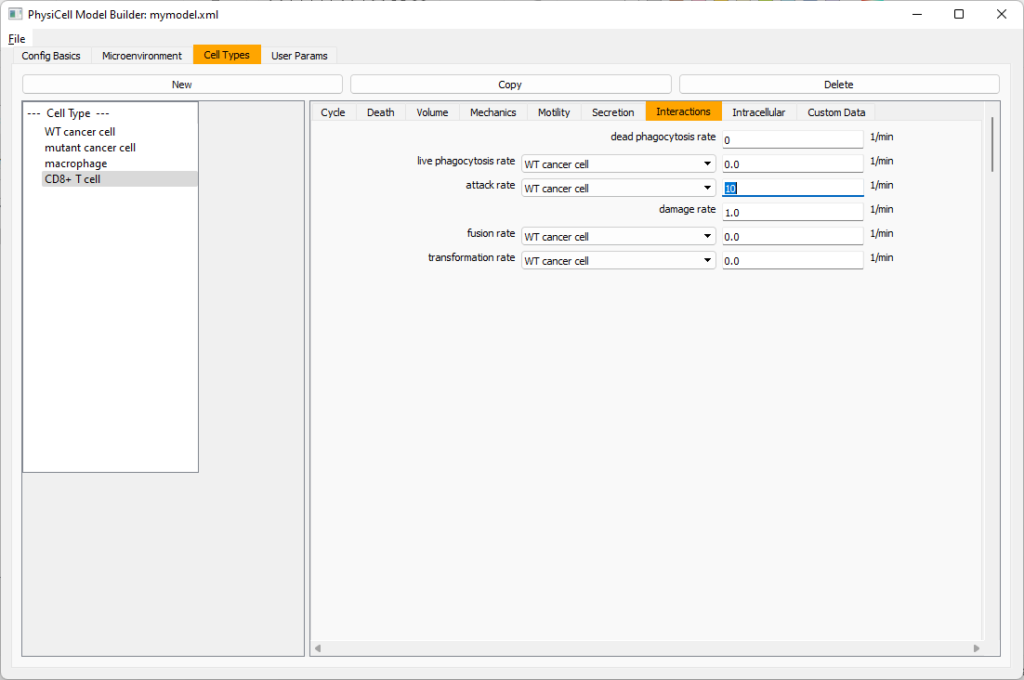
Lastly, let’s set these cells to attack WT and tumor cells. Go to the interactions tab. Set the dead phagocytosis rate to 0.
Now, let’s work on attack. Set the damage rate to 1.0. Near attack rate, choose WT tumor cell from the drop-down, and set its attack rate to 10 (so it attacks during any 0.1 minute interval). Then choose mutant tumor cell from the drop-down, and set its attack rate to 1 (as a model of immune evasion, where they are less likely to attack a non-WT tumor cell).
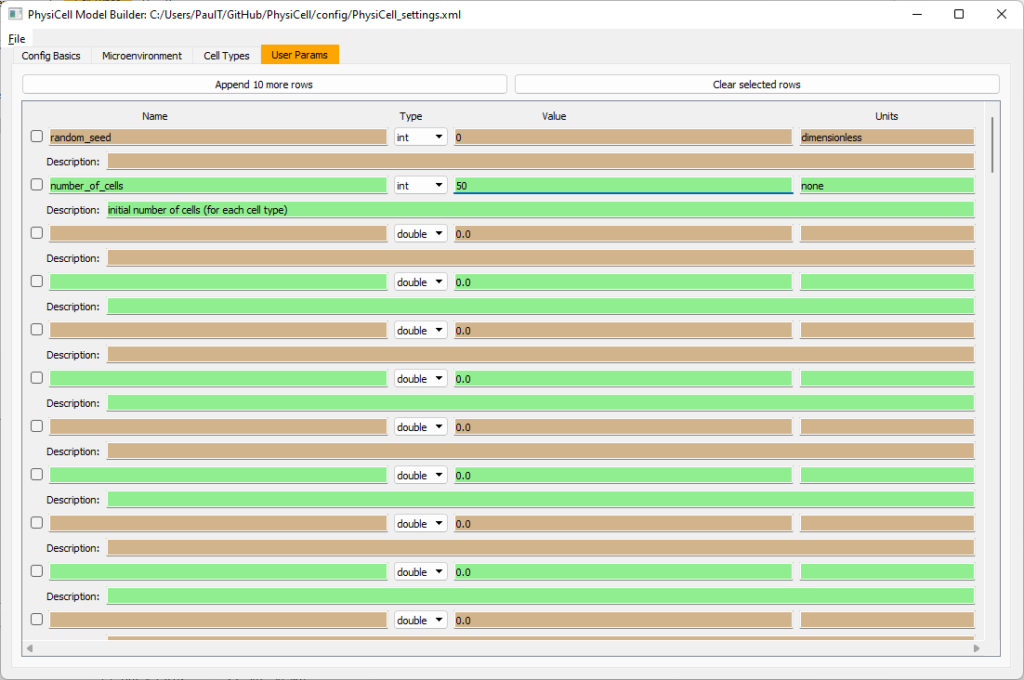
Set the initial cell conditions
Go to the user params tab. On number of cells, choose 50. It will randomly place 50 of each cell type at the start of the simulation.
That’s all! Go to File and save (or save as), and overwrite config/PhysiCell_settings.xml. Then close the model builder.
Testing the model
Go into the PhysiCell directory. Since you already compiled, just run your model (which will use PhysiCell_settings.xml that you just saved to the config directory). For Linux or MacOS (or similar Unix-like systems):
./project
Windows users would type project without the ./ at the front.
Take a look at your SVG outputs in the output directory. You might consider making an animated gif (make gif) or a movie:
make jpeg && make movie
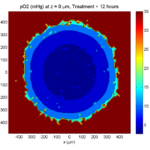
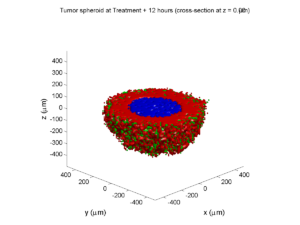
Here’s what we have.
 |
Promising! But we still need to write a little C++ so that damage kills tumor cells, and so that dead tumor cells release debris. (And we could stand to “anchor” tumor cells to ECM so they don’t get pushed around by the immune cells, but that’s a post for another day!)
Customizing the WT and mutant tumor cells with phenotype functions
First, open custom.h in the custom_modules directory, and declare a function for tumor phenotype:
void tumor_phenotype_function( Cell* pCell, Phenotype& phenotype, double dt );
Now, let’s open custom.cpp to write this function at the bottom. Here’s what we’ll do:
- If dead, set rate of debris release to 1.0 and return.
- Otherwise, we’ll set damage-based apoptosis.
- Get the base apoptosis rate
- Get the current damage
- Use a Hill response function with a half-max of 36, max apoptosis rate of 0.05 min\(^{-1}\), and a hill power of 2.0
Here’s the code:
void tumor_phenotype_function( Cell* pCell, Phenotype& phenotype, double dt )
{
// find my cell definition
static Cell_Definition* pCD = find_cell_definition( pCell->type_name );
// find the index of debris in the environment
static int nDebris = microenvironment.find_density_index( "debris" );
static int nTS = microenvironment.find_density_index( "tumor signal" );
// if dead: release debris. stop releasing tumor signal
if( phenotype.death.dead == true )
{
phenotype.secretion.secretion_rates[nDebris] = 1;
phenotype.secretion.saturation_densities[nDebris] = 1;
phenotype.secretion.secretion_rates[nTS] = 0;
// last time I'll execute this function (special optional trick)
pCell->functions.update_phenotype = NULL;
return;
}
// damage increases death
// find death model
static int nApoptosis =
phenotype.death.find_death_model_index( PhysiCell_constants::apoptosis_death_model );
double signal = pCell->state.damage; // current damage
double base_val = pCD->phenotype.death.rates[nApoptosis]; // base death rate (from cell def)
double max_val = 0.05; // max death rate (at large damage)
static double damage_halfmax = 36.0;
double hill_power = 2.0;
// evaluate Hill response function
double hill = Hill_response_function( signal , damage_halfmax , hill_power );
// set "dose-dependent" death rate
phenotype.death.rates[nApoptosis] = base_val + (max_val-base_val)*hill;
return;
}
Now, we need to make sure we apply these functions to tumor cell. Go to `create_cell_types` and look just before we display the cell definitions. We need to:
- Search for the WT tumor cell definition
- Set the update_phenotype function for that type to the tumor_phenotype_function we just wrote
- Repeat for the mutant tumor cell type.
Here’s the code:
...
/*
Put any modifications to individual cell definitions here.
This is a good place to set custom functions.
*/
cell_defaults.functions.update_phenotype = phenotype_function;
cell_defaults.functions.custom_cell_rule = custom_function;
cell_defaults.functions.contact_function = contact_function;
Cell_Definition* pCD = find_cell_definition( "WT cancer cell");
pCD->functions.update_phenotype = tumor_phenotype_function;
pCD = find_cell_definition( "mutant cancer cell");
pCD->functions.update_phenotype = tumor_phenotype_function;
/*
This builds the map of cell definitions and summarizes the setup.
*/
display_cell_definitions( std::cout );
return;
}
That’s it! Let’s recompile and run!
make && ./project
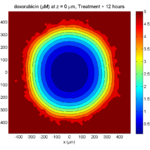
And here’s the final movie.
 |
Much better! Now the
Coming up next!
We will use the signal and behavior dictionaries to help us easily write C++ functions to modulate the tumor and immune cell behaviors.
Once ready, this will be posted at http://www.mathcancer.org/blog/introducing-cell-signal-and-behavior-dictionaries/.
PhysiCell Tools : python-loader
The newest tool for PhysiCell provides an easy way to load your PhysiCell output data into python for analysis. This builds upon previous work on loading data into MATLAB. A post on that tool can be found at:
http://www.mathcancer.org/blog/working-with-physicell-snapshots-in-matlab/.
PhysiCell stores output data as a MultiCell Digital Snapshot (MultiCellDS) that consists of several files for each time step and is probably stored in your ./output directory. pyMCDS is a python object that is initialized with the .xml file
What you’ll need
- python-loader, available on GitHub at
- Python 3.x, recommended distribution available at
- A number of Python packages, included in anaconda or available through pip
- NumPy
- pandas
- scipy
- Some PhysiCell data, probably in your ./output directory
Anatomy of a MultiCell Digital Snapshot
Each time PhysiCell’s internal time tracker passes a time step where data is to be saved, it generates a number of files of various types. Each of these files will have a number at the end that indicates where it belongs in the sequence of outputs. All of the files from the first round of output will end in 00000000.* and the second round will be 00000001.* and so on. Let’s say we’re interested in a set of output from partway through the run, the 88th set of output files. The files we care about most from this set consists of:
- output00000087.xml: This file is the main organizer of the data. It contains an overview of the data stored in the MultiCellDS as well as some actual data including:
- Metadata about the time and runtime for the current time step
- Coordinates for the computational domain
- Parameters for diffusing substrates in the microenvironment
- Column labels for the cell data
- File names for the files that contain microenvironment and cell data at this time step
- output00000087_microenvironment0.mat: This is a MATLAB matrix file that contains all of the data about the microenvironment at this time step
- output00000087_cells_physicell.mat: This is a MATLAB matrix file that contains all of the tracked information about the individual cells in the model. It tells us things like the cells’ position, volume, secretion, cell cycle status, and user-defined cell parameters.
Setup
Using pyMCDS
From the appropriate file in your PhysiCell directory, wherever pyMCDS.py lives, you can use the data loader in your own scripts or in an interactive session. To start you have to import the pyMCDS class
from pyMCDS import pyMCDS
Loading the data
Data is loaded into python from the MultiCellDS by initializing the pyMCDS object. The initialization function for pyMCDS takes one required and one optional argument.
__init__(xml_file, [output_path = '.'])
'''
xml_file : string
String containing the name of the output xml file
output_path :
String containing the path (relative or absolute) to the directory
where PhysiCell output files are stored
'''
We are interested in reading output00000087.xml that lives in ~/path/to/PhysiCell/output (don’t worry Windows paths work too). We would initialize our pyMCDS object using those names and the actual data would be stored in a member dictionary called data.
mcds = pyMCDS('output00000087.xml', '~/path/to/PhysiCell/output')
# Now our data lives in:
mcds.data
We’ve tried to keep everything organized inside of this dictionary but let’s take a look at what we actually have in here. Of course in real output, there will probably not be a chemical named my_chemical, this is simply there to illustrate how multiple chemicals are handled.
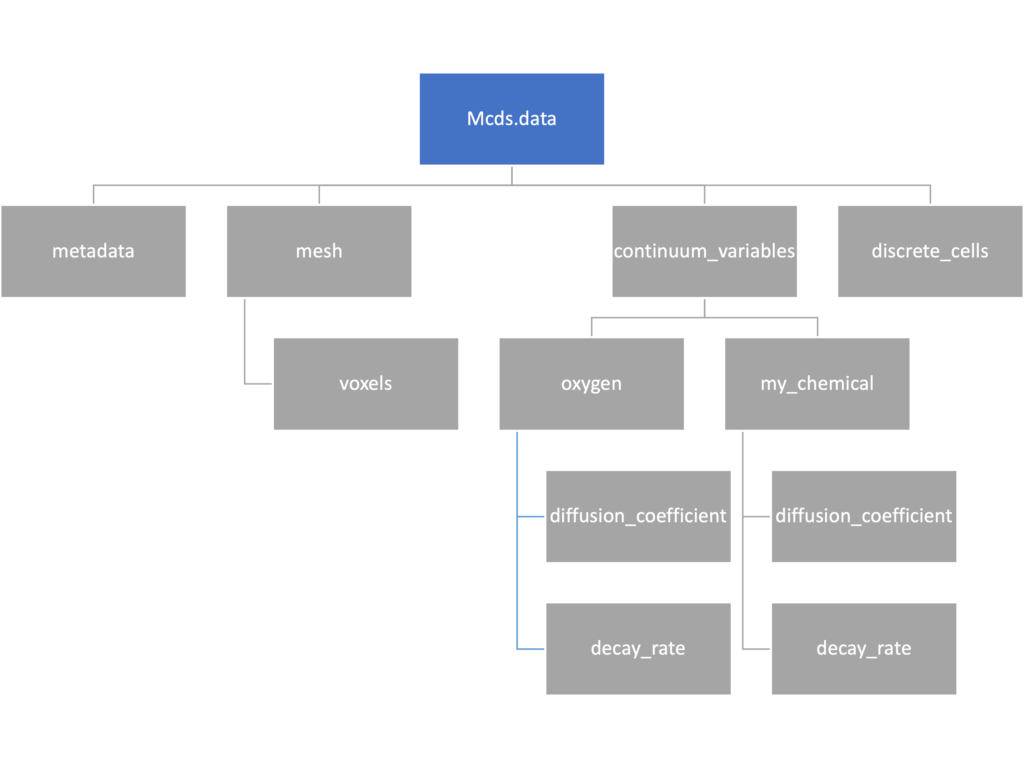
The data member dictionary is a dictionary of dictionaries whose child dictionaries can be accessed through normal python dictionary syntax.
mcds.data['metadata'] mcds.data['continuum_variables']['my_chemical']
Each of these subdictionaries contains data, we will take a look at exactly what that data is and how it can be accessed in the following sections.
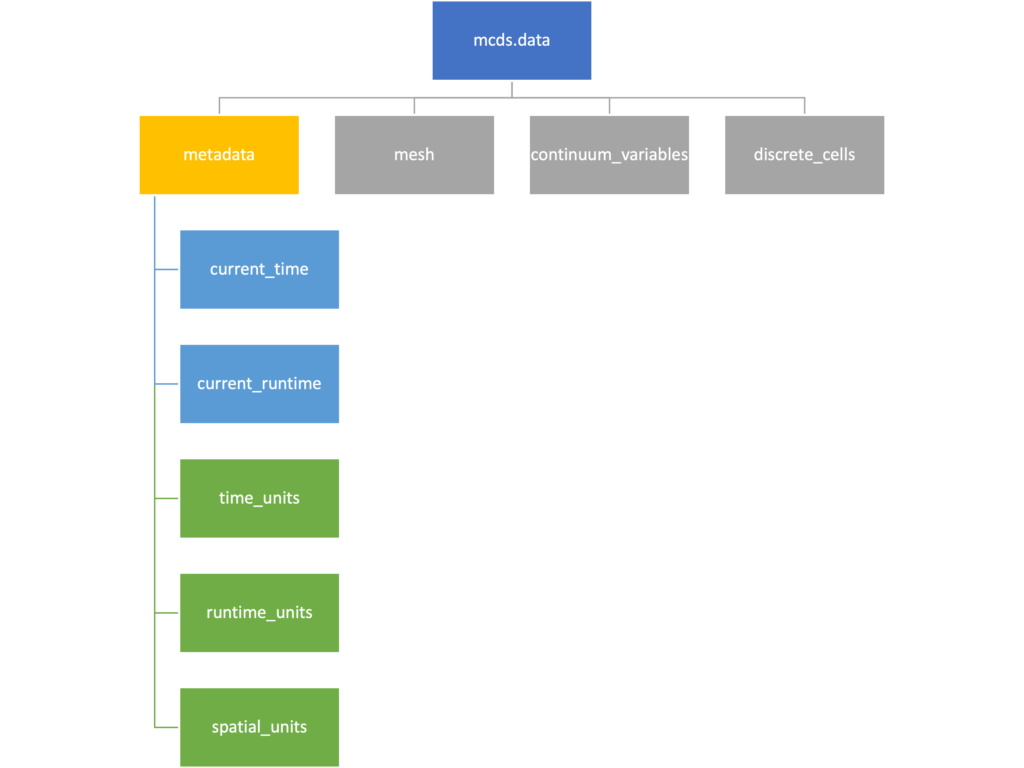
Metadata
The metadata dictionary contains information about the time of the simulation as well as units for both times and space. Here and in later sections blue boxes indicate scalars and green boxes indicate strings. We can access each of these things using normal dictionary syntax. We’ve also got access to a helper function get_time() for the common operation of retrieving the simulation time.
>>> mcds.data['metadata']['time_units'] 'min' >>> mcds.get_time() 5220.0
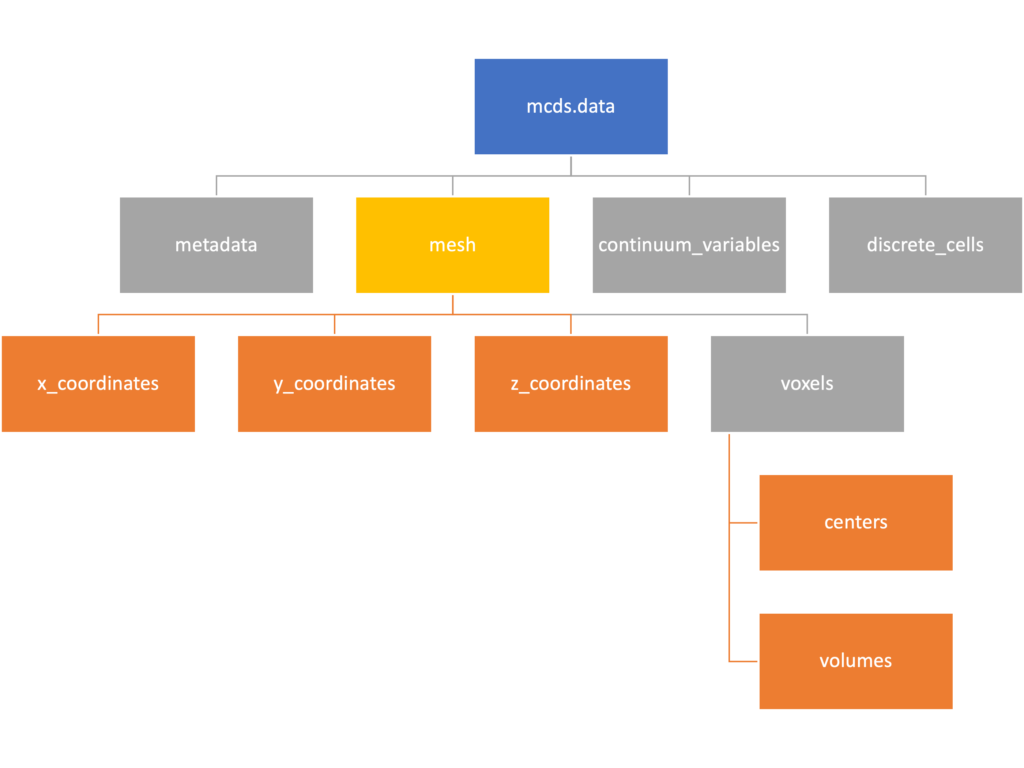
Mesh
The mesh dictionary has a lot more going on than the metadata dictionary. It contains three numpy arrays, indicated by orange boxes, as well as another dictionary. The three arrays contain \(x\), \(y\) and \(z\) coordinates for the centers of the voxels that constiture the computational domain in a meshgrid format. This means that each of those arrays is tensors of rank three. Together they identify the coordinates of each possible point in the space.
In contrast, the arrays in the voxel dictionary are stored linearly. If we know that we care about voxel number 42, we want to use the stuff in the voxels dictionary. If we want to make a contour plot, we want to use the x_coordinates, y_coordinates, and z_coordinates arrays.
# We can extract one of the meshgrid arrays as a numpy array
>>> y_coords = mcds.data['mesh']['y_coordinates']
>>> y_coords.shape
(75, 75, 75)
>>> y_coords[0, 0, :4]
array([-740., -740., -740., -740.])
# We can also extract the array of voxel centers
>>> centers = mcds.data['mesh']['voxels']['centers']
>>> centers.shape
(3, 421875)
>>> centers[:, :4]
array([[-740., -720., -700., -680.],
[-740., -740., -740., -740.],
[-740., -740., -740., -740.]])
# We have a handy function to quickly extract the components of the full meshgrid
>>> xx, yy, zz = mcds.get_mesh()
>>> yy.shape
(75, 75, 75)
>>> yy[0, 0, :4]
array([-740., -740., -740., -740.])
# We can also use this to return the meshgrid describing an x, y plane
>>> xx, yy = mcds.get_2D_mesh()
>>> yy.shape
(75, 75)
Continuum variables
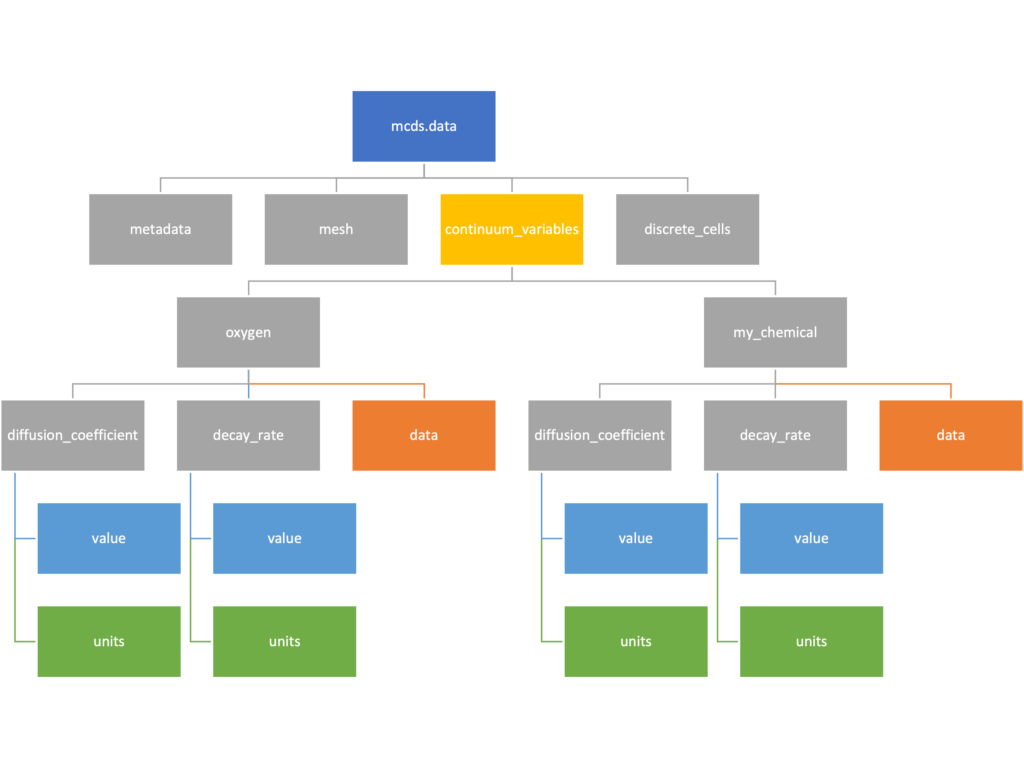
The continuum_variables dictionary is the most complicated of the four. It contains subdictionaries that we access using the names of each of the chemicals in the microenvironment. In our toy example above, these are oxygen and my_chemical. If our model tracked diffusing oxygen, VEGF, and glucose, then the continuum_variables dictionary would contain a subdirectory for each of them.
For a particular chemical species in the microenvironment we have two more dictionaries called decay_rate and diffusion_coefficient, and a numpy array called data. The diffusion and decay dictionaries each complete the value stored as a scalar and the unit stored as a string. The numpy array contains the concentrations of the chemical in each voxel at this time and is the same shape as the meshgrids of the computational domain stored in the .data[‘mesh’] arrays.
# we need to know the names of the substrates to work with
# this data. We have a function to help us find them.
>>> mcds.get_substrate_names()
['oxygen', 'my_chemical']
# The diffusable chemical dictionaries are messy
# if we need to do a lot with them it might be easier
# to put them into their own instance
>>> oxy_dict = mcds.data['continuum_variables']['oxygen']
>>> oxy_dict['decay_rate']
{'value': 0.1, 'units': '1/min'}
# What we care about most is probably the numpy
# array of concentrations
>>> oxy_conc = oxy_dict['data']
>>> oxy_conc.shape
(75, 75, 75)
# Alternatively, we can get the same array with a function
>>> oxy_conc2 = mcds.get_concentrations('oxygen')
>>> oxy_conc2.shape
(75, 75, 75)
# We can also get the concentrations on a plane using the
# same function and supplying a z value to "slice through"
# note that right now the z_value must be an exact match
# for a plane of voxel centers, in the future we may add
# interpolation.
>>> oxy_plane = mcds.get_concentrations('oxygen', z_value=100.0)
>>> oxy_plane.shape
(75, 75)
# we can also find the concentration in a single voxel using the
# position of a point within that voxel. This will give us an
# array of all concentrations at that point.
>>> mcds.get_concentrations_at(x=0., y=550., z=0.)
array([17.94514446, 0.99113448])
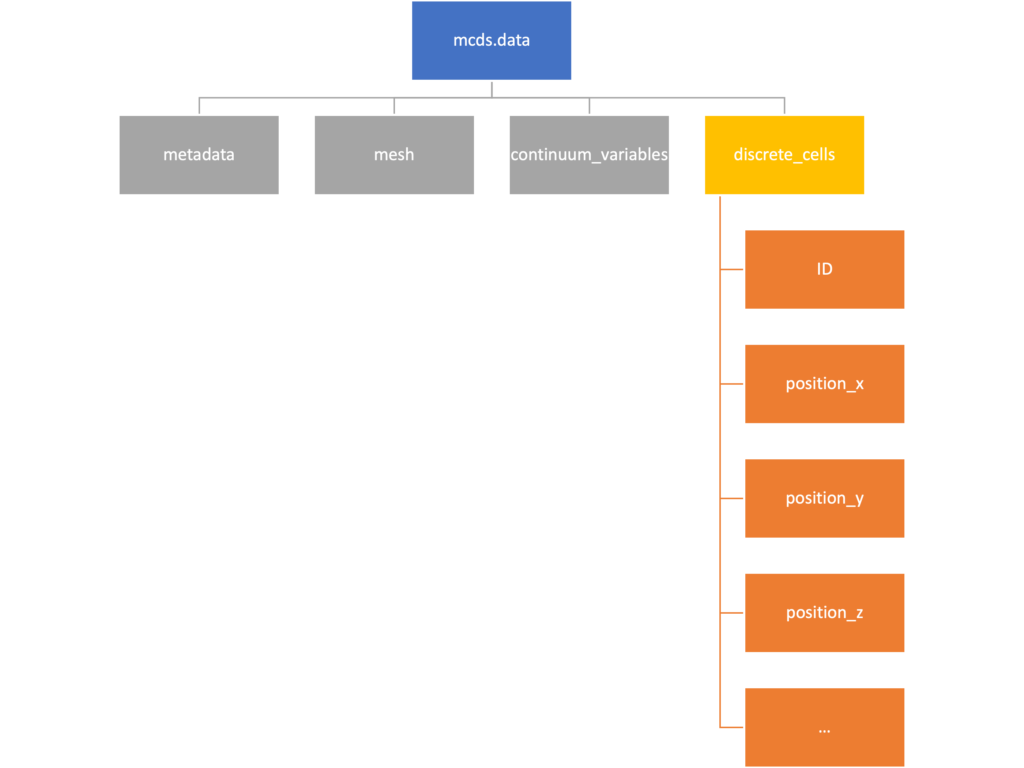
Discrete Cells
The discrete cells dictionary is relatively straightforward. It contains a number of numpy arrays that contain information regarding individual cells. These are all 1-dimensional arrays and each corresponds to one of the variables specified in the output*.xml file. With the default settings, these are:
- ID: unique integer that will identify the cell throughout its lifetime in the simulation
- position(_x, _y, _z): floating point positions for the cell in \(x\), \(y\), and \(z\) directions
- total_volume: total volume of the cell
- cell_type: integer label for the cell as used in PhysiCell
- cycle_model: integer label for the cell cycle model as used in PhysiCell
- current_phase: integer specification for which phase of the cycle model the cell is currently in
- elapsed_time_in_phase: time that cell has been in current phase of cell cycle model
- nuclear_volume: volume of cell nucleus
- cytoplasmic_volume: volume of cell cytoplasm
- fluid_fraction: proportion of the volume due to fliud
- calcified_fraction: proportion of volume consisting of calcified material
- orientation(_x, _y, _z): direction in which cell is pointing
- polarity:
- migration_speed: current speed of cell
- motility_vector(_x, _y, _z): current direction of movement of cell
- migration_bias: coefficient for stochastic movement (higher is “more deterministic”)
- motility_bias_direction(_x, _y, _z): direction of movement bias
- persistence_time: time in-between direction changes for cell
- motility_reserved:
# Extracting single variables is just like before
>>> cell_ids = mcds.data['discrete_cells']['ID']
>>> cell_ids.shape
(18595,)
>>> cell_ids[:4]
array([0., 1., 2., 3.])
# If we're clever we can extract 2D arrays
>>> cell_vec = np.zeros((cell_ids.shape[0], 3))
>>> vec_list = ['position_x', 'position_y', 'position_z']
>>> for i, lab in enumerate(vec_list):
... cell_vec[:, i] = mcds.data['discrete_cells'][lab]
...
array([[ -69.72657128, -39.02046405, -233.63178904],
[ -69.84507464, -22.71693265, -233.59277388],
[ -69.84891462, -6.04070516, -233.61816711],
[ -69.845265 , 10.80035554, -233.61667313]])
# We can get the list of all of the variables stored in this dictionary
>>> mcds.get_cell_variables()
['ID',
'position_x',
'position_y',
'position_z',
'total_volume',
'cell_type',
'cycle_model',
'current_phase',
'elapsed_time_in_phase',
'nuclear_volume',
'cytoplasmic_volume',
'fluid_fraction',
'calcified_fraction',
'orientation_x',
'orientation_y',
'orientation_z',
'polarity',
'migration_speed',
'motility_vector_x',
'motility_vector_y',
'motility_vector_z',
'migration_bias',
'motility_bias_direction_x',
'motility_bias_direction_y',
'motility_bias_direction_z',
'persistence_time',
'motility_reserved',
'oncoprotein',
'elastic_coefficient',
'kill_rate',
'attachment_lifetime',
'attachment_rate']
# We can also get all of the cell data as a pandas DataFrame
>>> cell_df = mcds.get_cell_df()
>>> cell_df.head()
ID position_x position_y position_z total_volume cell_type cycle_model ...
0.0 - 69.726571 - 39.020464 - 233.631789 2494.0 0.0 5.0 ...
1.0 - 69.845075 - 22.716933 - 233.592774 2494.0 0.0 5.0 ...
2.0 - 69.848915 - 6.040705 - 233.618167 2494.0 0.0 5.0 ...
3.0 - 69.845265 10.800356 - 233.616673 2494.0 0.0 5.0 ...
4.0 - 69.828161 27.324530 - 233.631579 2494.0 0.0 5.0 ...
# if we want to we can also get just the subset of cells that
# are in a specific voxel
>>> vox_df = mcds.get_cell_df_at(x=0.0, y=550.0, z=0.0)
>>> vox_df.iloc[:, :5]
ID position_x position_y position_z total_volume
26718 228761.0 6.623617 536.709341 -1.282934 2454.814507
52736 270274.0 -7.990034 538.184921 9.648955 1523.386488
Examples
These examples will not be made using our toy dataset described above but will instead be made using a single timepoint dataset that can be found at:
Substrate contour plot
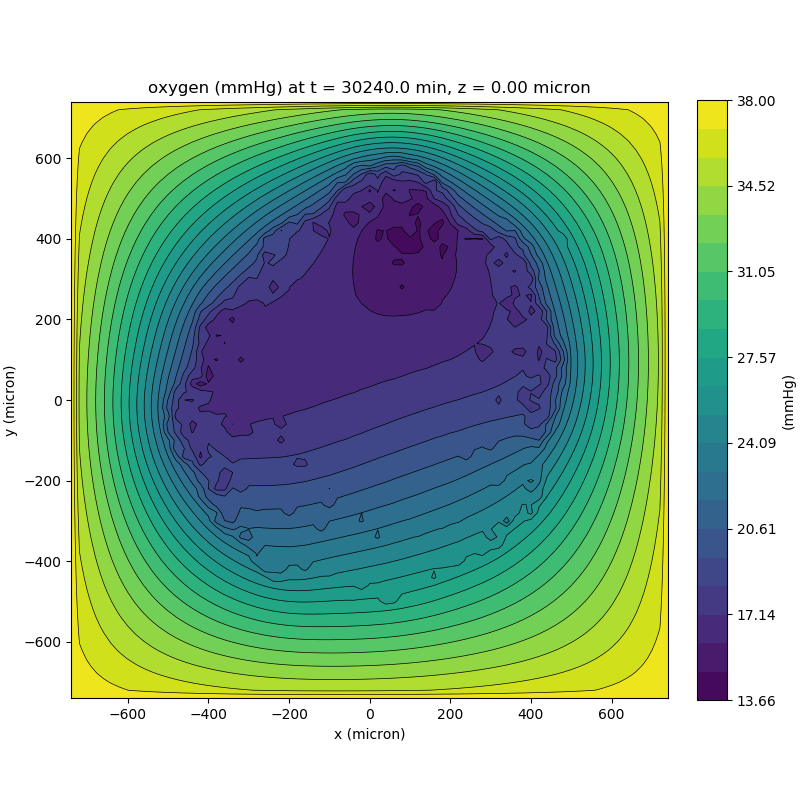
One of the big advantages of working with PhysiCell data in python is that we have access to its plotting tools. For the sake of example let’s plot the partial pressure of oxygen throughout the computational domain along the \(z = 0\) plane. Once we’ve loaded our data by initializing a pyMCDS object, we can work entirely within python to produce the plot.
from pyMCDS import pyMCDS
import numpy as np
import matplotlib.pyplot as plt
# load data
mcds = pyMCDS('output00003696.xml', '../output')
# Set our z plane and get our substrate values along it
z_val = 0.00
plane_oxy = mcds.get_concentrations('oxygen', z_slice=z_val)
# Get the 2D mesh for contour plotting
xx, yy = mcds.get_mesh()
# We want to be able to control the number of contour levels so we
# need to do a little set up
num_levels = 21
min_conc = plane_oxy.min()
max_conc = plane_oxy.max()
my_levels = np.linspace(min_conc, max_conc, num_levels)
# set up the figure area and add data layers
fig, ax = plt.subplot()
cs = ax.contourf(xx, yy, plane_oxy, levels=my_levels)
ax.contour(xx, yy, plane_oxy, color='black', levels = my_levels,
linewidths=0.5)
# Now we need to add our color bar
cbar1 = fig.colorbar(cs, shrink=0.75)
cbar1.set_label('mmHg')
# Let's put the time in to make these look nice
ax.set_aspect('equal')
ax.set_xlabel('x (micron)')
ax.set_ylabel('y (micron)')
ax.set_title('oxygen (mmHg) at t = {:.1f} {:s}, z = {:.2f} {:s}'.format(
mcds.get_time(),
mcds.data['metadata']['time_units'],
z_val,
mcds.data['metadata']['spatial_units'])
plt.show()
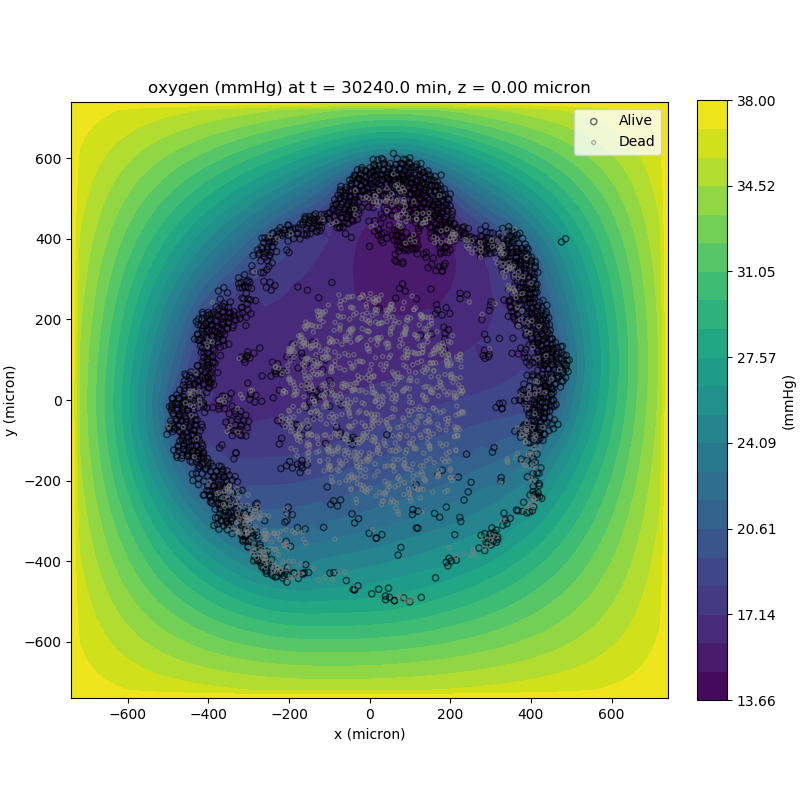
Adding a cells layer
We can also use pandas to do fairly complex selections of cells to add to our plots. Below we use pandas and the previous plot to add a cells layer.
from pyMCDS import pyMCDS
import numpy as np
import matplotlib.pyplot as plt
# load data
mcds = pyMCDS('output00003696.xml', '../output')
# Set our z plane and get our substrate values along it
z_val = 0.00
plane_oxy = mcds.get_concentrations('oxygen', z_slice=z_val)
# Get the 2D mesh for contour plotting
xx, yy = mcds.get_mesh()
# We want to be able to control the number of contour levels so we
# need to do a little set up
num_levels = 21
min_conc = plane_oxy.min()
max_conc = plane_oxy.max()
my_levels = np.linspace(min_conc, max_conc, num_levels)
# get our cells data and figure out which cells are in the plane
cell_df = mcds.get_cell_df()
ds = mcds.get_mesh_spacing()
inside_plane = (cell_df['position_z'] < z_val + ds) \ & (cell_df['position_z'] > z_val - ds)
plane_cells = cell_df[inside_plane]
# We're going to plot two types of cells and we want it to look nice
colors = ['black', 'grey']
sizes = [20, 8]
labels = ['Alive', 'Dead']
# set up the figure area and add microenvironment layer
fig, ax = plt.subplot()
cs = ax.contourf(xx, yy, plane_oxy, levels=my_levels)
# get our cells of interest
# alive_cells = plane_cells[plane_cells['cycle_model'] < 6]
# dead_cells = plane_cells[plane_cells['cycle_model'] > 6]
# -- for newer versions of PhysiCell
alive_cells = plane_cells[plane_cells['cycle_model'] < 100]
dead_cells = plane_cells[plane_cells['cycle_model'] >= 100]
# plot the cell layer
for i, plot_cells in enumerate((alive_cells, dead_cells)):
ax.scatter(plot_cells['position_x'].values,
plot_cells['position_y'].values,
facecolor='none',
edgecolors=colors[i],
alpha=0.6,
s=sizes[i],
label=labels[i])
# Now we need to add our color bar
cbar1 = fig.colorbar(cs, shrink=0.75)
cbar1.set_label('mmHg')
# Let's put the time in to make these look nice
ax.set_aspect('equal')
ax.set_xlabel('x (micron)')
ax.set_ylabel('y (micron)')
ax.set_title('oxygen (mmHg) at t = {:.1f} {:s}, z = {:.2f} {:s}'.format(
mcds.get_time(),
mcds.data['metadata']['time_units'],
z_val,
mcds.data['metadata']['spatial_units'])
ax.legend(loc='upper right')
plt.show()
Future Direction
The first extension of this project will be timeseries functionality. This will provide similar data loading functionality but for a time series of MultiCell Digital Snapshots instead of simply one point in time.
PhysiCell Tools : PhysiCell-povwriter
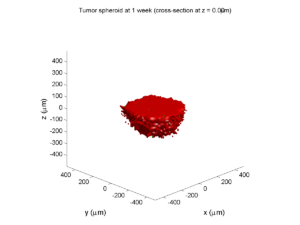
As PhysiCell matures, we are starting to turn our attention to better training materials and an ecosystem of open source PhysiCell tools. PhysiCell-povwriter is is designed to help transform your 3-D simulation results into 3-D visualizations like this one:
PhysiCell-povwriter transforms simulation snapshots into 3-D scenes that can be rendered into still images using POV-ray: an open source software package that uses raytracing to mimic the path of light from a source of illumination to a single viewpoint (a camera or an eye). The result is a beautifully rendered scene (at any resolution you choose) with very nice shading and lighting.
If you repeat this on many simulation snapshots, you can create an animation of your work.
What you’ll need
This workflow is entirely based on open source software:
- 3-D simulation data (likely stored in ./output from your project)
- PhysiCell-povwriter, available on GitHub at
- POV-ray, available at
- ImageMagick (optional, for image file conversions)
- mencoder (optional, for making compressed movies)
Setup
Building PhysiCell-povwriter
After you clone PhysiCell-povwriter or download its source from a release, you’ll need to compile it. In the project’s root directory, compile the project by:
make
(If you need to set up a C++ PhysiCell development environment, click here for OSX or here for Windows.)
Next, copy povwriter (povwriter.exe in Windows) to either the root directory of your PhysiCell project, or somewhere in your path. Copy ./config/povwriter-settings.xml to the ./config directory of your PhysiCell project.
Editing resolutions in POV-ray
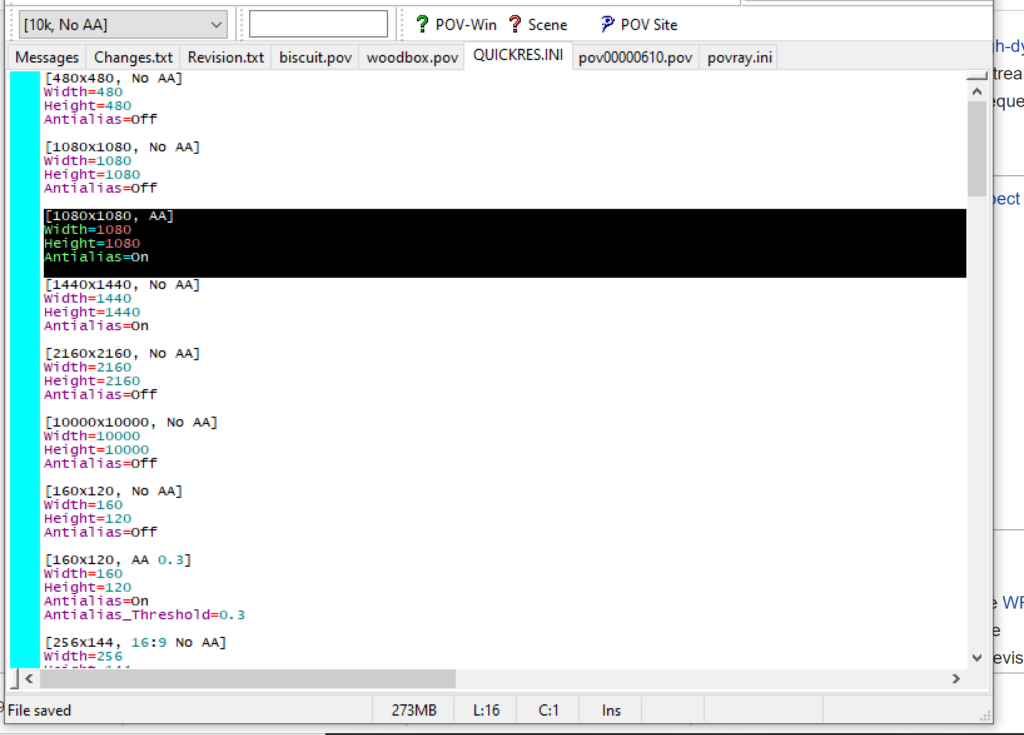
PhysiCell-povwriter is intended for creating “square” images, but POV-ray does not have any pre-created square rendering resolutions out-of-the-box. However, this is straightforward to fix.
- Open POV-Ray
- Go to the “tools” menu and select “edit resolution INI file”
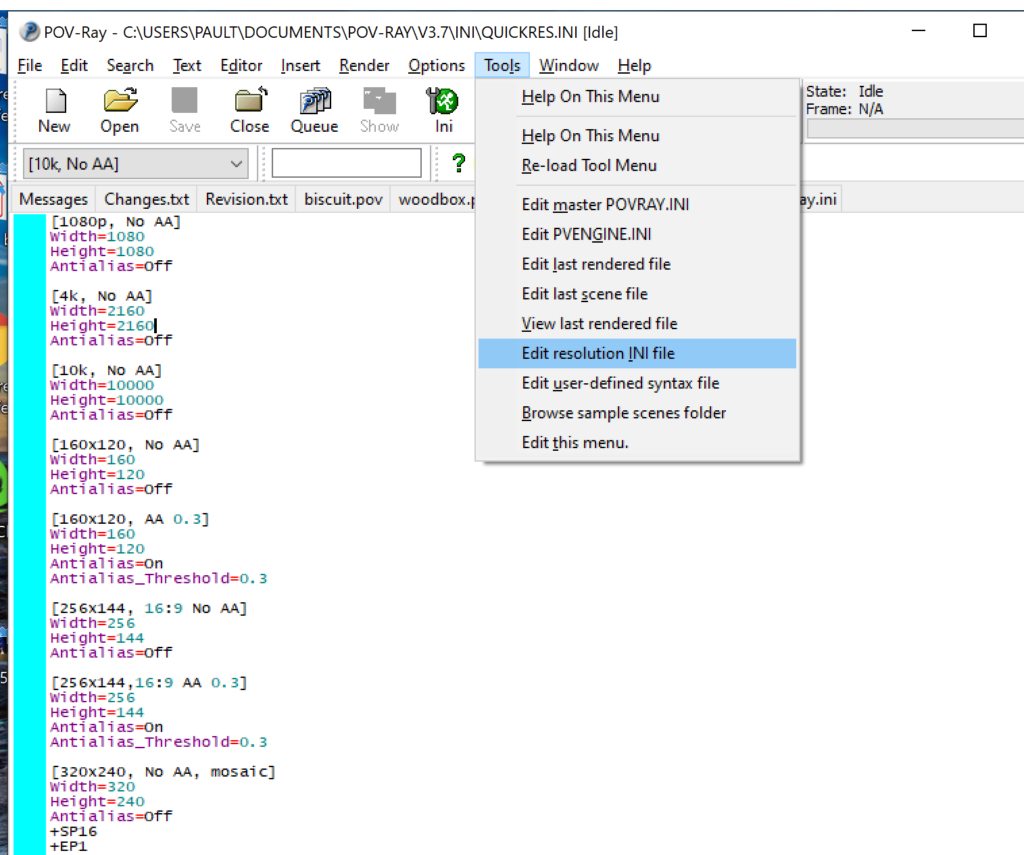
- At the top of the INI file (which opens for editing in POV-ray), make a new profile:
[1080x1080, AA] Width=480 Height=480 Antialias=On
- Make similar profiles (with unique names) to suit your preferences. I suggest one at 480×480 (as a fast preview), another at 2160×2160, and another at 5000×5000 (because they will be absurdly high resolution). For example:
[2160x2160 no AA] Width=2160 Height=2160 Antialias=Off
You can optionally make more profiles with antialiasing on (which provides some smoothing for areas of high detail), but you’re probably better off just rendering without antialiasing at higher resolutions and the scaling the image down as needed. Also, rendering without antialiasing will be faster.
- Once done making profiles, save and exit POV-Ray.
- The next time you open POV-Ray, your new resolution profiles will be available in the lefthand dropdown box.
Configuring PhysiCell-povwriter
Once you have copied povwriter-settings.xml to your project’s config file, open it in a text editor. Below, we’ll show the different settings.
Camera settings
<camera> <distance_from_origin units="micron">1500</distance_from_origin> <xy_angle>3.92699081699</xy_angle> <!-- 5*pi/4 --> <yz_angle>1.0471975512</yz_angle> <!-- pi/3 --> </camera>
For simplicity, PhysiCell-POVray (currently) always aims the camera towards the origin (0,0,0), with “up” towards the positive z-axis. distance_from_origin sets how far the camera is placed from the origin. xy_angle sets the angle \(\theta\) from the positive x-axis in the xy-plane. yz_angle sets the angle \(\phi\) from the positive z-axis in the yz-plane. Both angles are in radians.
Options
<options> <use_standard_colors>true</use_standard_colors> <nuclear_offset units="micron">0.1</nuclear_offset> <cell_bound units="micron">750</cell_bound> <threads>8</threads> </options>
use_standard_colors (if set to true) uses a built-in “paint-by-numbers” color scheme, where each cell type (identified with an integer) gets XML-defined colors for live, apoptotic, and dead cells. More on this below. If use_standard_colors is set to false, then PhysiCell-povwriter uses the my_pigment_and_finish_function in ./custom_modules/povwriter.cpp to color cells.
The nuclear_offset is a small additional height given to nuclei when cropping to avoid visual artifacts when rendering (which can cause some “tearing” or “bleeding” between the rendered nucleus and cytoplasm). cell_bound is used for leaving some cells out of bound: any cell with |x|, |y|, or |z| exceeding cell_bound will not be rendered. threads is used for parallelizing on multicore processors; note that it only speeds up povwriter if you are converting multiple PhysiCell outputs to povray files.
Save
<save> <!-- done --> <folder>output</folder> <!-- use . for root --> <filebase>output</filebase> <time_index>3696</time_index> </save>
Use folder to tell PhysiCell-povwriter where the data files are stored. Use filebase to tell how the outputs are named. Typically, they have the form output########_cells_physicell.mat; in this case, the filebase is output. Lastly, use time_index to set the output number. For example if your file is output00000182_cells_physicell.mat, then filebase = output and time_index = 182.
Below, we’ll see how to specify ranges of indices at the command line, which would supersede the time_index given here in the XML.
Clipping planes
PhysiCell-povwriter uses clipping planes to help create cutaway views of the simulations. By default, 3 clipping planes are used to cut out an octant of the viewing area.
Recall that a plane can be defined by its normal vector n and a point p on the plane. With these, the plane can be defined as all points x satisfying
\[ \left( \vec{x} -\vec{p} \right) \cdot \vec{n} = 0 \]
These are then written out as a plane equation
\[ a x + by + cz + d = 0, \]
where
\[ (a,b,c) = \vec{n} \hspace{.5in} \textrm{ and } \hspace{0.5in} d = \: – \vec{n} \cdot \vec{p}. \]
As of Version 1.0.0, we are having some difficulties with clipping planes that do not pass through the origin (0,0,0), for which \( d = 0 \).
In the config file, these planes are written as \( (a,b,c,d) \):
<clipping_planes> <!-- done --> <clipping_plane>0,-1,0,0</clipping_plane> <clipping_plane>-1,0,0,0</clipping_plane> <clipping_plane>0,0,1,0</clipping_plane> </clipping_planes>
Note that cells “behind” the plane (where \( ( \vec{x} – \vec{p} ) \cdot \vec{n} \le 0 \)) are rendered, and cells in “front” of the plane (where \( (\vec{x}-\vec{p}) \cdot \vec{n} > 0 \)) are not rendered. Cells that intersect the plane are partially rendered (using constructive geometry via union and intersection commands in POV-ray).
Cell color definitions
Within <cell_color_definitions>, you’ll find multiple <cell_colors> blocks, each of which defines the live, dead, and necrotic colors for a specific cell type (with the type ID indicated in the attribute). These colors are only applied if use_standard_colors is set to true in options. See above.
The live colors are given as two rgb (red,green,blue) colors for the cytoplasm and nucleus of live cells. Each element of this triple can range from 0 to 1, and not from 0 to 255 as in many raw image formats. Next, finish specifies ambient (how much highly-scattered background ambient light illuminates the cell), diffuse (how well light rays can illuminate the surface), and specular (how much of a shiny reflective splotch the cell gets).
See the POV-ray documentation for for information on the finish.
This is repeated to give the apoptotic and necrotic colors for the cell type.
<cell_colors type="0"> <live> <cytoplasm>.25,1,.25</cytoplasm> <!-- red,green,blue --> <nuclear>0.03,0.125</nuclear> <finish>0.05,1,0.1</finish> <!-- ambient,diffuse,specular --> </live> <apoptotic> <cytoplasm>1,0,0</cytoplasm> <!-- red,green,blue --> <nuclear>0.125,0,0</nuclear> <finish>0.05,1,0.1</finish> <!-- ambient,diffuse,specular --> </apoptotic> <necrotic> <cytoplasm>1,0.5412,0.1490</cytoplasm> <!-- red,green,blue --> <nuclear>0.125,0.06765,0.018625</nuclear> <finish>0.01,0.5,0.1</finish> <!-- ambient,diffuse,specular --> </necrotic> </cell_colors>
Use multiple cell_colors blocks (each with type corresponding to the integer cell type) to define the colors of multiple cell types.
Using PhysiCell-povwriter
Use by the XML configuration file alone
The simplest syntax:
physicell$ ./povwriter
(Windows users: povwriter or povwriter.exe) will process ./config/povwriter-settings.xml and convert the single indicated PhysiCell snapshot to a .pov file.
If you run POV-writer with the default configuration file in the povwriter structure (with the supplied sample data), it will render time index 3696 from the immunotherapy example in our 2018 PhysiCell Method Paper:
physicell$ ./povwriter povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Processing file ./output/output00003696_cells_physicell.mat... Matrix size: 32 x 66978 Creating file pov00003696.pov for output ... Writing 66978 cells ... done! Done processing all 1 files!
The result is a single POV-ray file (pov00003696.pov) in the root directory.
Now, open that file in POV-ray (double-click the file if you are in Windows), choose one of your resolutions in your lefthand dropdown (I’ll choose 2160×2160 no antialiasing), and click the green “run” button.
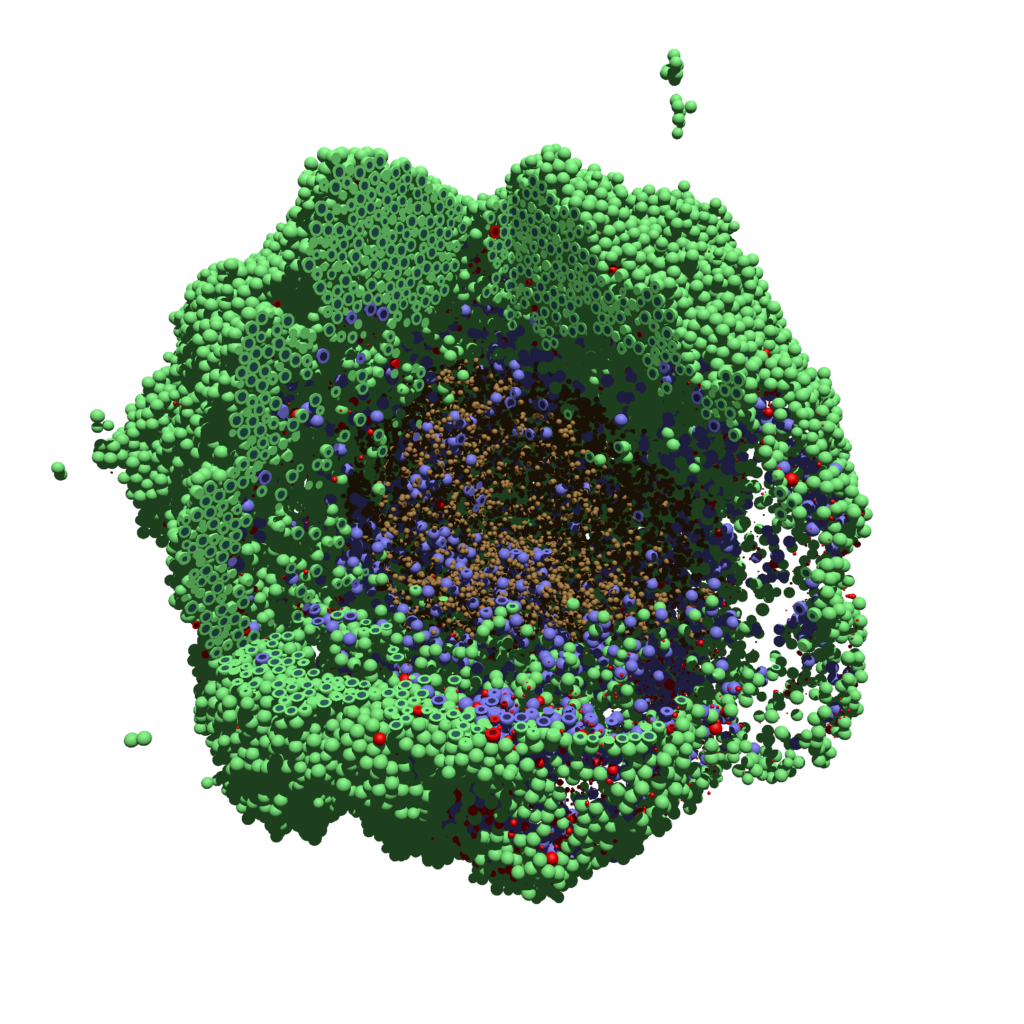
You can watch the image as it renders. The result should be a PNG file (named pov00003696.png) that looks like this:
Using command-line options to process multiple times (option #1)
Now, suppose we have more outputs to process. We still state most of the options in the XML file as above, but now we also supply a command-line argument in the form of start:interval:end. If you’re still in the povwriter project, note that we have some more sample data there. Let’s grab and process it:
physicell$ cd output physicell$ unzip more_samples.zip Archive: more_samples.zip inflating: output00000000_cells_physicell.mat inflating: output00000001_cells_physicell.mat inflating: output00000250_cells_physicell.mat inflating: output00000300_cells_physicell.mat inflating: output00000500_cells_physicell.mat inflating: output00000750_cells_physicell.mat inflating: output00001000_cells_physicell.mat inflating: output00001250_cells_physicell.mat inflating: output00001500_cells_physicell.mat inflating: output00001750_cells_physicell.mat inflating: output00002000_cells_physicell.mat inflating: output00002250_cells_physicell.mat inflating: output00002500_cells_physicell.mat inflating: output00002750_cells_physicell.mat inflating: output00003000_cells_physicell.mat inflating: output00003250_cells_physicell.mat inflating: output00003500_cells_physicell.mat inflating: output00003696_cells_physicell.mat physicell$ ls citation and license.txt more_samples.zip output00000000_cells_physicell.mat output00000001_cells_physicell.mat output00000250_cells_physicell.mat output00000300_cells_physicell.mat output00000500_cells_physicell.mat output00000750_cells_physicell.mat output00001000_cells_physicell.mat output00001250_cells_physicell.mat output00001500_cells_physicell.mat output00001750_cells_physicell.mat output00002000_cells_physicell.mat output00002250_cells_physicell.mat output00002500_cells_physicell.mat output00002750_cells_physicell.mat output00003000_cells_physicell.mat output00003250_cells_physicell.mat output00003500_cells_physicell.mat output00003696.xml output00003696_cells_physicell.mat
Let’s go back to the parent directory and run povwriter:
physicell$ ./povwriter 0:250:3500 povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Matrix size: 32 x 18317 Processing file ./output/output00000000_cells_physicell.mat... Creating file pov00000000.pov for output ... Writing 18317 cells ... Processing file ./output/output00002000_cells_physicell.mat... Matrix size: 32 x 33551 Creating file pov00002000.pov for output ... Writing 33551 cells ... Processing file ./output/output00002500_cells_physicell.mat... Matrix size: 32 x 43440 Creating file pov00002500.pov for output ... Writing 43440 cells ... Processing file ./output/output00001500_cells_physicell.mat... Matrix size: 32 x 40267 Creating file pov00001500.pov for output ... Writing 40267 cells ... Processing file ./output/output00003000_cells_physicell.mat... Matrix size: 32 x 56659 Creating file pov00003000.pov for output ... Writing 56659 cells ... Processing file ./output/output00001000_cells_physicell.mat... Matrix size: 32 x 74057 Creating file pov00001000.pov for output ... Writing 74057 cells ... Processing file ./output/output00003500_cells_physicell.mat... Matrix size: 32 x 66791 Creating file pov00003500.pov for output ... Writing 66791 cells ... Processing file ./output/output00000500_cells_physicell.mat... Matrix size: 32 x 114316 Creating file pov00000500.pov for output ... Writing 114316 cells ... done! Processing file ./output/output00000250_cells_physicell.mat... Matrix size: 32 x 75352 Creating file pov00000250.pov for output ... Writing 75352 cells ... done! Processing file ./output/output00002250_cells_physicell.mat... Matrix size: 32 x 37959 Creating file pov00002250.pov for output ... Writing 37959 cells ... done! Processing file ./output/output00001750_cells_physicell.mat... Matrix size: 32 x 32358 Creating file pov00001750.pov for output ... Writing 32358 cells ... done! Processing file ./output/output00002750_cells_physicell.mat... Matrix size: 32 x 49658 Creating file pov00002750.pov for output ... Writing 49658 cells ... done! Processing file ./output/output00003250_cells_physicell.mat... Matrix size: 32 x 63546 Creating file pov00003250.pov for output ... Writing 63546 cells ... done! done! done! done! Processing file ./output/output00001250_cells_physicell.mat... Matrix size: 32 x 54771 Creating file pov00001250.pov for output ... Writing 54771 cells ... done! done! done! done! Processing file ./output/output00000750_cells_physicell.mat... Matrix size: 32 x 97642 Creating file pov00000750.pov for output ... Writing 97642 cells ... done! done! Done processing all 15 files!
Notice that the output appears a bit out of order. This is normal: povwriter is using 8 threads to process 8 files at the same time, and sending some output to the single screen. Since this is all happening simultaneously, it’s a bit jumbled (and non-sequential). Don’t panic. You should now have created pov00000000.pov, pov00000250.pov, … , pov00003500.pov.
Now, go into POV-ray, and choose “queue.” Click “Add File” and select all 15 .pov files you just created:
Hit “OK” to let it render all the povray files to create PNG files (pov00000000.png, … , pov00003500.png).
Using command-line options to process multiple times (option #2)
You can also give a list of indices. Here’s how we render time indices 250, 1000, and 2250:
physicell$ ./povwriter 250,1000,2250 povwriter version 1.0.0 ================================================================================ Copyright (c) Paul Macklin 2019, on behalf of the PhysiCell project OSI License: BSD-3-Clause (see LICENSE.txt) Usage: ================================================================================ povwriter : run povwriter with config file ./config/settings.xml povwriter FILENAME.xml : run povwriter with config file FILENAME.xml povwriter x:y:z : run povwriter on data in FOLDER with indices from x to y in incremenets of z Example: ./povwriter 0:2:10 processes files: ./FOLDER/FILEBASE00000000_physicell_cells.mat ./FOLDER/FILEBASE00000002_physicell_cells.mat ... ./FOLDER/FILEBASE00000010_physicell_cells.mat (See the config file to set FOLDER and FILEBASE) povwriter x1,...,xn : run povwriter on data in FOLDER with indices x1,...,xn Example: ./povwriter 1,3,17 processes files: ./FOLDER/FILEBASE00000001_physicell_cells.mat ./FOLDER/FILEBASE00000003_physicell_cells.mat ./FOLDER/FILEBASE00000017_physicell_cells.mat (Note that there are no spaces.) (See the config file to set FOLDER and FILEBASE) Code updates at https://github.com/PhysiCell-Tools/PhysiCell-povwriter Tutorial & documentation at http://MathCancer.org/blog/povwriter ================================================================================ Using config file ./config/povwriter-settings.xml ... Using standard coloring function ... Found 3 clipping planes ... Found 2 cell color definitions ... Processing file ./output/output00002250_cells_physicell.mat... Matrix size: 32 x 37959 Creating file pov00002250.pov for output ... Writing 37959 cells ... Processing file ./output/output00001000_cells_physicell.mat... Matrix size: 32 x 74057 Creating file pov00001000.pov for output ... Processing file ./output/output00000250_cells_physicell.mat... Matrix size: 32 x 75352 Writing 74057 cells ... Creating file pov00000250.pov for output ... Writing 75352 cells ... done! done! done! Done processing all 3 files!
This will create files pov00000250.pov, pov00001000.pov, and pov00002250.pov. Render them in POV-ray just as before.
Advanced options (at the source code level)
If you set use_standard_colors to false, povwriter uses the function my_pigment_and_finish_function (at the end of ./custom_modules/povwriter.cpp). Make sure that you set colors.cyto_pigment (RGB) and colors.nuclear_pigment (also RGB). The source file in povwriter has some hinting on how to write this. Note that the XML files saved by PhysiCell have a legend section that helps you do determine what is stored in each column of the matlab file.
Optional postprocessing
Image conversion / manipulation with ImageMagick
Suppose you want to convert the PNG files to JPEGs, and scale them down to 60% of original size. That’s very straightforward in ImageMagick:
physicell$ magick mogrify -format jpg -resize 60% pov*.png
Creating an animated GIF with ImageMagick
Suppose you want to create an animated GIF based on your images. I suggest first converting to JPG (see above) and then using ImageMagick again. Here, I’m adding a 20 ms delay between frames:
physicell$ magick convert -delay 20 *.jpg out.gif
Here’s the result:

Creating a compressed movie with Mencoder
Syntax coming later.
Closing thoughts and future work
In the future, we will probably allow more control over the clipping planes and a bit more debugging on how to handle planes that don’t pass through the origin. (First thoughts: we need to change how we use union and intersection commands in the POV-ray outputs.)
We should also look at adding some transparency for the cells. I’d prefer something like rgba (red-green-blue-alpha), but POV-ray uses filters and transmission, and we want to make sure to get it right.
Lastly, it would be nice to find a balance between the current very simple camera setup and better control.
Thanks for reading this PhysiCell Friday tutorial! Please do give PhysiCell at try (at http://PhysiCell.org) and read the method paper at PLoS Computational Biology.
A small computational thought experiment
In Macklin (2017), I briefly touched on a simple computational thought experiment that shows that for a group of homogeneous cells, you can observe substantial heterogeneity in cell behavior. This “thought experiment” is part of a broader preview and discussion of a fantastic paper by Linus Schumacher, Ruth Baker, and Philip Maini published in Cell Systems, where they showed that a migrating collective homogeneous cells can show heterogeneous behavior when quantitated with new migration metrics. I highly encourage you to check out their work!
In this blog post, we work through my simple thought experiment in a little more detail.
Note: If you want to reference this blog post, please cite the Cell Systems preview article:
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
The thought experiment
Consider a simple (and widespread) model of a population of cycling cells: each virtual cell (with index i) has a single “oncogene” \( r_i \) that sets the rate of progression through the cycle. Between now (t) and a small time from now ( \(t+\Delta t\)), the virtual cell has a probability \(r_i \Delta t\) of dividing into two daughter cells. At the population scale, the overall population growth model that emerges from this simple single-cell model is:
\[\frac{dN}{dt} = \langle r\rangle N, \]
where \( \langle r \rangle \) the mean division rate over the cell population, and N is the number of cells. See the discussion in the supplementary information for Macklin et al. (2012).
Now, suppose (as our thought experiment) that we could track individual cells in the population and track how long it takes them to divide. (We’ll call this the division time.) What would the distribution of cell division times look like, and how would it vary with the distribution of the single-cell rates \(r_i\)?
Mathematical method
In the Matlab script below, we implement this cell cycle model as just about every discrete model does. Here’s the pseudocode:
t = 0;
while( t < t_max )
for i=1:Cells.size()
u = random_number();
if( u < Cells[i].birth_rate * dt )
Cells[i].division_time = Cells[i].age;
Cells[i].divide();
end
end
t = t+dt;
end
That is, until we’ve reached the final simulation time, loop through all the cells and decide if they should divide: For each cell, choose a random number between 0 and 1, and if it’s smaller than the cell’s division probability (\(r_i \Delta t\)), then divide the cell and write down the division time.
As an important note, we have to track the same cells until they all divide, rather than merely record which cells have divided up to the end of the simulation. Otherwise, we end up with an observational bias that throws off our recording. See more below.
The sample code
You can download the Matlab code for this example at:
http://MathCancer.org/files/matlab/thought_experiment_matlab(Macklin_Cell_Systems_2017).zip
Extract all the files, and run “thought_experiment” in Matlab (or Octave, if you don’t have a Matlab license or prefer an open source platform) for the main result.
All these Matlab files are available as open source, under the GPL license (version 3 or later).
Results and discussion
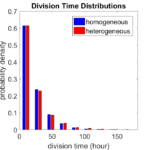
First, let’s see what happens if all the cells are identical, with \(r = 0.05 \textrm{ hr}^{-1}\). We run the script, and track the time for each of 10,000 cells to divide. As expected by theory (Macklin et al., 2012) (but perhaps still a surprise if you haven’t looked), we get an exponential distribution of division times, with mean time \(1/\langle r \rangle\):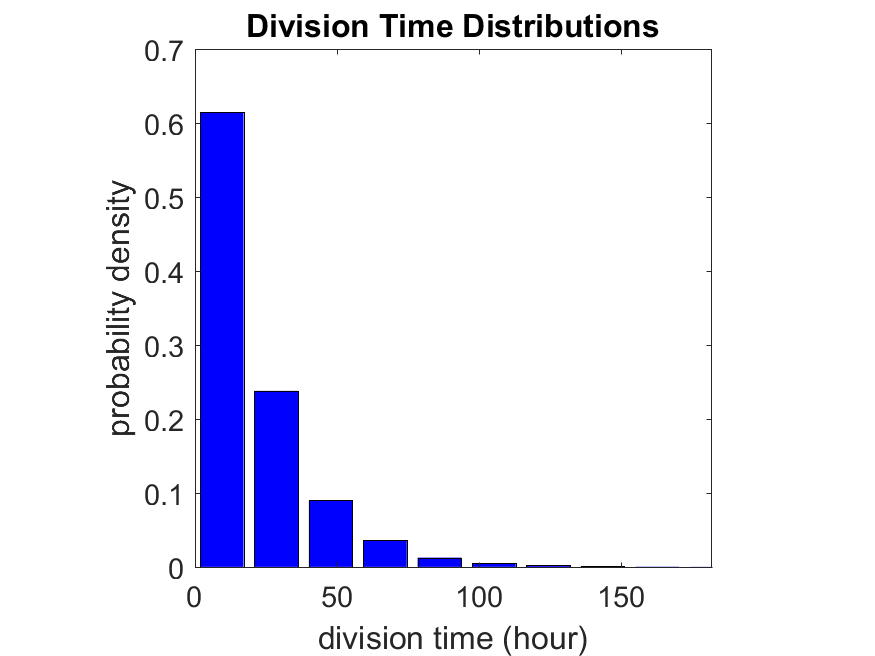
So even in this simple model, a homogeneous population of cells can show heterogeneity in their behavior. Here’s the interesting thing: let’s now give each cell its own division parameter \(r_i\) from a normal distribution with mean \(0.05 \textrm{ hr}^{-1}\) and a relative standard deviation of 25%: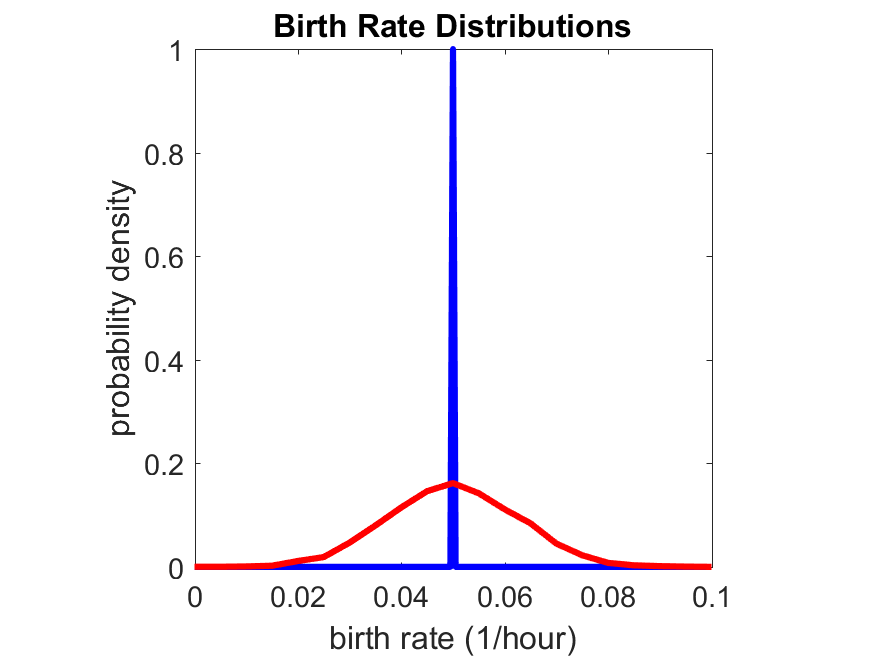
If we repeat the experiment, we get the same distribution of cell division times!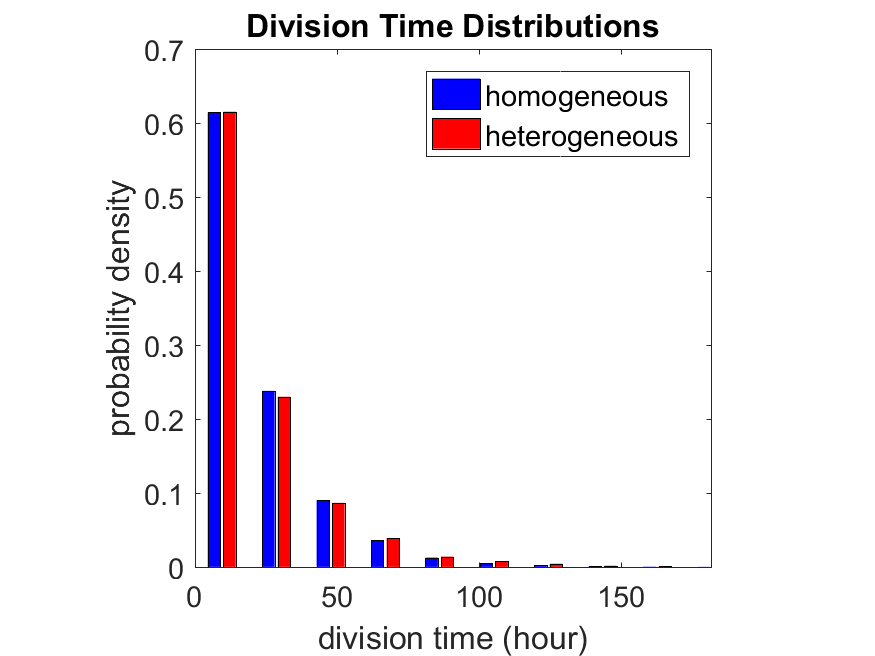
So in this case, based solely on observations of the phenotypic heterogeneity (the division times), it is impossible to distinguish a “genetically” homogeneous cell population (one with identical parameters) from a truly heterogeneous population. We would require other metrics, like tracking changes in the mean division time as cells with a higher \(r_i\) out-compete the cells with lower \(r_i\).
Lastly, I want to point out that caution is required when designing these metrics and single-cell tracking. If instead we had tracked all cells throughout the simulated experiment, including new daughter cells, and then recorded the first 10,000 cell division events, we would get a very different distribution of cell division times: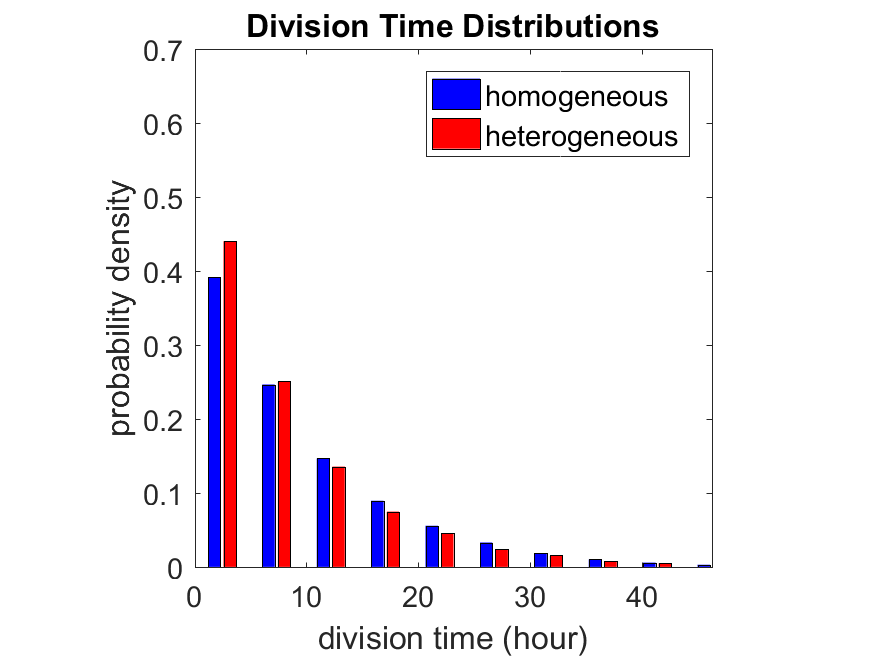
By only recording the division times for the cells that have divided, and not those that haven’t, we bias our observations towards cells with shorter division times. Indeed, the mean division time for this simulated experiment is far lower than we would expect by theory. You can try this one by running “bad_thought_experiment”.
Further reading
This post is an expansion of our recent preview in Cell Systems in Macklin (2017):
P. Macklin, When seeing isn’t believing: How math can guide our interpretation of measurements and experiments. Cell Sys., 2017 (in press). DOI: 10.1016/j.cells.2017.08.005
And the original work on apparent heterogeneity in collective cell migration is by Schumacher et al. (2017):
L. Schumacher et al., Semblance of Heterogeneity in Collective Cell Migration. Cell Sys., 2017 (in press). DOI: 10.1016/j.cels.2017.06.006
You can read some more on relating exponential distributions and Poisson processes to common discrete mathematical models of cell populations in Macklin et al. (2012):
P. Macklin, et al., Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): From microscopic measurements to macroscopic predictions of clinical progression. J. Theor. Biol. 301:122-40, 2012. DOI: 10.1016/j.jtbi.2012.02.002.
Lastly, I’d be delighted if you took a look at the open source software we have been developing for 3-D simulations of multicellular systems biology:
http://OpenSource.MathCancer.org
And you can always keep up-to-date by following us on Twitter: @MathCancer.
MathCancer C++ Style and Practices Guide
As PhysiCell, BioFVM, and other open source projects start to gain new users and contributors, it’s time to lay out a coding style. We have three goals here:
- Consistency: It’s easier to understand and contribute to the code if it’s written in a consistent way.
- Readability: We want the code to be as readable as possible.
- Reducing errors: We want to avoid coding styles that are more prone to errors. (e.g., code that can be broken by introducing whitespace).
So, here is the guide (revised June 2017). I expect to revise this guide from time to time.
Place braces on separate lines in functions and classes.
I find it much easier to read a class if the braces are on separate lines, with good use of whitespace. Remember: whitespace costs almost nothing, but reading and understanding (and time!) are expensive.
DON’T
class Cell{
public:
double some_variable;
bool some_extra_variable;
Cell(); };
class Phenotype{
public:
double some_variable;
bool some_extra_variable;
Phenotype();
};
DO:
class Cell
{
public:
double some_variable;
bool some_extra_variable;
Cell();
};
class Phenotype
{
public:
double some_variable;
bool some_extra_variable;
Phenotype();
};
Enclose all logic in braces, even when optional.
In C/C++, you can omit the curly braces in some cases. For example, this is legal
if( distance > 1.5*cell_radius )
interaction = false;
force = 0.0; // is this part of the logic, or a separate statement?
error = false;
However, this code is ambiguous to interpret. Moreover, small changes to whitespace–or small additions to the logic–could mess things up here. Use braces to make the logic crystal clear:
DON’T
if( distance > 1.5*cell_radius )
interaction = false;
force = 0.0; // is this part of the logic, or a separate statement?
error = false;
if( condition1 == true )
do_something1 = true;
elseif( condition2 == true )
do_something2 = true;
else
do_something3 = true;
DO
if( distance > 1.5*cell_radius )
{
interaction = false;
force = 0.0;
}
error = false;
if( condition1 == true )
{ do_something1 = true; }
elseif( condition2 == true )
{ do_something2 = true; }
else
{ do_something3 = true; }
Put braces on separate lines in logic, except for single-line logic.
This style rule relates to the previous point, to improve readability.
DON’T
if( distance > 1.5*cell_radius ){
interaction = false;
force = 0.0; }
if( condition1 == true ){ do_something1 = true; }
elseif( condition2 == true ){
do_something2 = true; }
else
{ do_something3 = true; error = true; }
DO
if( distance > 1.5*cell_radius )
{
interaction = false;
force = 0.0;
}
if( condition1 == true )
{ do_something1 = true; } // this is fine
elseif( condition2 == true )
{
do_something2 = true; // this is better
}
else
{
do_something3 = true;
error = true;
}
See how much easier that code is to read? The logical structure is crystal clear, and adding more to the logic is simple.
End all functions with a return, even if void.
For clarity, definitively state that a function is done by using return.
DON’T
void my_function( Cell& cell )
{
cell.phenotype.volume.total *= 2.0;
cell.phenotype.death.rates[0] = 0.02;
// Are we done, or did we forget something?
// is somebody still working here?
}
DO
void my_function( Cell& cell )
{
cell.phenotype.volume.total *= 2.0;
cell.phenotype.death.rates[0] = 0.02;
return;
}
Use tabs to indent the contents of a class or function.
This is to make the code easier to read. (Unfortunately PHP/HTML makes me use five spaces here instead of tabs.)
DON’T
class Secretion
{
public:
std::vector<double> secretion_rates;
std::vector<double> uptake_rates;
std::vector<double> saturation_densities;
};
void my_function( Cell& cell )
{
cell.phenotype.volume.total *= 2.0;
cell.phenotype.death.rates[0] = 0.02;
return;
}
DO
class Secretion
{
public:
std::vector<double> secretion_rates;
std::vector<double> uptake_rates;
std::vector<double> saturation_densities;
};
void my_function( Cell& cell )
{
cell.phenotype.volume.total *= 2.0;
cell.phenotype.death.rates[0] = 0.02;
return;
}
Use a single space to indent public and other keywords in a class.
This gets us some nice formatting in classes, without needing two tabs everywhere.
DON’T
class Secretion
{
public:
std::vector<double> secretion_rates;
std::vector<double> uptake_rates;
std::vector<double> saturation_densities;
}; // not enough whitespace
class Errors
{
private:
std::string none_of_your_business
public:
std::string error_message;
int error_code;
}; // too much whitespace!
DO
class Secretion
{
private:
public:
std::vector<double> secretion_rates;
std::vector<double> uptake_rates;
std::vector<double> saturation_densities;
};
class Errors
{
private:
std::string none_of_your_business
public:
std::string error_message;
int error_code;
};
Avoid arcane operators, when clear logic statements will do.
It can be difficult to decipher code with statements like this:
phenotype.volume.fluid=phenotype.volume.fluid<0?0:phenotype.volume.fluid;
Moreover, C and C++ can treat precedence of ternary operators very differently, so subtle bugs can creep in when using the “fancier” compact operators. Variations in how these operators work across languages are an additional source of error for programmers switching between languages in their daily scientific workflows. Wherever possible (and unless there is a significant performance reason to do so), use clear logical structures that are easy to read even if you only dabble in C/C++. Compiler-time optimizations will most likely eliminate any performance gains from these goofy operators.
DON’T
// if the fluid volume is negative, set it to zero phenotype.volume.fluid=phenotype.volume.fluid<0.0?0.0:pCell->phenotype.volume.fluid;
DO
if( phenotype.volume.fluid < 0.0 )
{
phenotype.volume.fluid = 0.0;
}
Here’s the funny thing: the second logic is much clearer, and it took fewer characters, even with extra whitespace for readability!
Pass by reference where possible.
Passing by reference is a great way to boost performance: we can avoid (1) allocating new temporary memory, (2) copying data into the temporary memory, (3) passing the temporary data to the function, and (4) deallocating the temporary memory once finished.
DON’T
double some_function( Cell cell )
{
return = cell.phenotype.volume.total + 3.0;
}
// This copies cell and all its member data!
DO
double some_function( Cell& cell )
{
return = cell.phenotype.volume.total + 3.0;
}
// This just accesses the original cell data without recopying it.
Where possible, pass by reference instead of by pointer.
There is no performance advantage to passing by pointers over passing by reference, but the code is simpler / clearer when you can pass by reference. It makes code easier to write and understand if you can do so. (If nothing else, you save yourself character of typing each time you can replace “->” by “.”!)
DON’T
double some_function( Cell* pCell )
{
return = pCell->phenotype.volume.total + 3.0;
}
// Writing and debugging this code can be error-prone.
DO
double some_function( Cell& cell )
{
return = cell.phenotype.volume.total + 3.0;
}
// This is much easier to write.
Be careful with static variables. Be thread safe!
PhysiCell relies heavily on parallelization by OpenMP, and so you should write functions under the assumption that they may be executed many times simultaneously. One easy source of errors is in static variables:
DON’T
double some_function( Cell& cell )
{
static double four_pi = 12.566370614359172;
static double output;
output = cell.phenotype.geometry.radius;
output *= output;
output *= four_pi;
return output;
}
// If two instances of some_function are running, they will both modify
// the *same copy* of output
DO
double some_function( Cell& cell )
{
static double four_pi = 12.566370614359172;
double output;
output = cell.phenotype.geometry.radius;
output *= output;
output *= four_pi;
return output;
}
// If two instances of some_function are running, they will both modify
// the their own copy of output, but still use the more efficient, once-
// allocated copy of four_pi. This one is safe for OpenMP.
Use std:: instead of “using namespace std”
PhysiCell uses the BioFVM and PhysiCell namespaces to avoid potential collision with other codes. Other codes using PhysiCell may use functions that collide with the standard namespace. So, we formally use std:: whenever using functions in the standard namespace.
DON’T
using namespace std; cout << "Hi, Mom, I learned to code today!" << endl; string my_string = "Cheetos are good, but Doritos are better."; cout << my_string << endl; vector<double> my_vector; vector.resize( 3, 0.0 );
DO
std::cout << "Hi, Mom, I learned to code today!" << std::endl; std::string my_string = "Cheetos are good, but Doritos are better."; std::cout << my_string << std::endl; std::vector<double> my_vector; my_vector.resize( 3, 0.0 );
Camelcase is ugly. Use underscores.
This is purely an aesthetic distinction, but CamelCaseCodeIsUglyAndDoYouUseDNAorDna?
DON’T
double MyVariable1; bool ProteinsInExosomes; int RNAtranscriptionCount; void MyFunctionDoesSomething( Cell& ImmuneCell );
DO
double my_variable1; bool proteins_in_exosomes; int RNA_transcription_count; void my_function_does_something( Cell& immune_cell );
Use capital letters to declare a class. Use lowercase for instances.
To help in readability and consistency, declare classes with capital letters (but no camelcase), and use lowercase for instances of those classes.
DON’T
class phenotype;
class cell
{
public:
std::vector<double> position;
phenotype Phenotype;
};
class ImmuneCell : public cell
{
public:
std::vector<double> surface_receptors;
};
void do_something( cell& MyCell , ImmuneCell& immuneCell );
cell Cell;
ImmuneCell MyImmune_cell;
do_something( Cell, MyImmune_cell );
DO
class Phenotype;
class Cell
{
public:
std::vector<double> position;
Phenotype phenotype;
};
class Immune_Cell : public Cell
{
public:
std::vector<double> surface_receptors;
};
void do_something( Cell& my_cell , Immune_Cell& immune_cell );
Cell cell;
Immune_Cell my_immune_cell;
do_something( cell, my_immune_cell );
Building a Cellular Automaton Model Using BioFVM
Note: This is part of a series of “how-to” blog posts to help new users and developers of BioFVM. See below for guides to setting up a C++ compiler in Windows or OSX.
What you’ll need
- A working C++ development environment with support for OpenMP. See these prior tutorials if you need help.
- A download of BioFVM, available at http://BioFVM.MathCancer.org and http://BioFVM.sf.net. Use Version 1.1.4 or later.
- The source code for this project (see below).
Matlab or Octave for visualization. Matlab might be available for free at your university. Octave is open source and available from a variety of sources.
Our modeling task
We will implement a basic 3-D cellular automaton model of tumor growth in a well-mixed fluid, containing oxygen pO2 (mmHg) and a drug c (e.g., doxorubicin, μM), inspired by modeling by Alexander Anderson, Heiko Enderling, Jan Poleszczuk, Gibin Powathil, and others. (I highly suggest seeking out the sophisticated cellular automaton models at Moffitt’s Integrated Mathematical Oncology program!) This example shows you how to extend BioFVM into a new cellular automaton model. I’ll write a similar post on how to add BioFVM into an existing cellular automaton model, which you may already have available.
Tumor growth will be driven by oxygen availability. Tumor cells can be live, apoptotic (going through energy-dependent cell death, or necrotic (undergoing death from energy collapse). Drug exposure can both trigger apoptosis and inhibit cell cycling. We will model this as growth into a well-mixed fluid, with pO2 = 38 mmHg (about 5% oxygen: a physioxic value) and c = 5 μM.
Mathematical model
As a cellular automaton model, we will divide 3-D space into a regular lattice of voxels, with length, width, and height of 15 μm. (A typical breast cancer cell has radius around 9-10 μm, giving a typical volume around 3.6×103 μm3. If we make each lattice site have the volume of one cell, this gives an edge length around 15 μm.)
In voxels unoccupied by cells, we approximate a well-mixed fluid with Dirichlet nodes, setting pO2 = 38 mmHg, and initially setting c = 0. Whenever a cell dies, we replace it with an empty automaton, with no Dirichlet node. Oxygen and drug follow the typical diffusion-reaction equations:
\[ \frac{ \partial \textrm{pO}_2 }{\partial t} = D_\textrm{oxy} \nabla^2 \textrm{pO}_2 – \lambda_\textrm{oxy} \textrm{pO}_2 – \sum_{ \textrm{cells} i} U_{i,\textrm{oxy}} \textrm{pO}_2 \]
\[ \frac{ \partial c}{ \partial t } = D_c \nabla^2 c – \lambda_c c – \sum_{\textrm{cells }i} U_{i,c} c \]
where each uptake rate is applied across the cell’s volume. We start the treatment by setting c = 5 μM on all Dirichlet nodes at t = 504 hours (21 days). For simplicity, we do not model drug degradation (pharmacokinetics), to approximate the in vitro conditions.
In any time interval [t,t+Δt], each live tumor cell i has a probability pi,D of attempting division, probability pi,A of apoptotic death, and probability pi,N of necrotic death. (For simplicity, we ignore motility in this version.) We relate these to the birth rate bi, apoptotic death rate di,A, and necrotic death rate di,N by the linearized equations (from Macklin et al. 2012):
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes apoptotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,A}(t) \Delta t\Bigr) \approx d_{i,A}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ attempts division in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -b_i(t) \Delta t\Bigr) \approx b_{i}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{cell } i \textrm{ becomes necrotic in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -d_{i,N}(t) \Delta t\Bigr) \approx d_{i,N}\Delta t \]
\[ \textrm{Prob} \Bigl( \textrm{dead cell } i \textrm{ lyses in } [t,t+\Delta t] \Bigr) = 1 – \textrm{exp}\Bigl( -\frac{1}{T_{i,D}} \Delta t\Bigr) \approx \frac{ \Delta t}{T_{i,D}} \]
(Illustrative) parameter values
We use Doxy = 105 μm2/min (Ghaffarizadeh et al. 2016), and we set Ui,oxy = 20 min-1 (to give an oxygen diffusion length scale of about 70 μm, with steeper gradients than our typical 100 μm length scale). We set λoxy = 0.01 min-1 for a 1 mm diffusion length scale in fluid.
We set Dc = 300 μm2/min, and Uc = 7.2×10-3 min-1 (Dc from Weinberg et al. (2007), and Ui,c twice as large as the reference value in Weinberg et al. (2007) to get a smaller diffusion length scale of about 204 μm). We set λc = 3.6×10-5 min-1 to give a drug diffusion length scale of about 2.9 mm in fluid.
We use TD = 8.6 hours for apoptotic cells, and TD = 60 days for necrotic cells (Macklin et al., 2013). However, note that necrotic and apoptotic cells lose volume quickly, so one may want to revise those time scales to match the point where a cell loses 90% of its volume.
Functional forms for the birth and death rates
We model pharmacodynamics with an area-under-the-curve (AUC) type formulation. If c(t) is the drug concentration at any cell i‘s location at time t, then let its integrated exposure Ei(t) be
\[ E_i(t) = \int_0^t c(s) \: ds \]
and we model its response with a Hill function
\[ R_i(t) = \frac{ E_i^h(t) }{ \alpha_i^h + E_i^h(t) }, \]
where h is the drug’s Hill exponent for the cell line, and α is the exposure for a half-maximum effect.
We model the microenvironment-dependent birth rate by:
\[ b_i(t) = \left\{ \begin{array}{lr} b_{i,P} \left( 1 – \eta_i R_i(t) \right) & \textrm{ if } \textrm{pO}_{2,P} < \textrm{pO}_2 \\ \\ b_{i,P} \left( \frac{\textrm{pO}_{2}-\textrm{pO}_{2,N}}{\textrm{pO}_{2,P}-\textrm{pO}_{2,N}}\right) \Bigl( 1 – \eta_i R_i(t) \Bigr) & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_2 \le \textrm{pO}_{2,P} \\ \\ 0 & \textrm{ if } \textrm{pO}_2 \le \textrm{pO}_{2,N}\end{array} \right. \]
where pO2,P is the physioxic oxygen value (38 mmHg), and pO2,N is a necrotic threshold (we use 5 mmHg), and 0 < η < 1 the drug’s birth inhibition. (A fully cytostatic drug has η = 1.)
We model the microenvironment-dependent apoptosis rate by:
\[ d_{i,A}(t) = d_{i,A}^* + \Bigl( d_{i,A}^\textrm{max} – d_{i,A}^* \Bigr) R_i(t) \]
\[ d_{i,N}(t) = \left\{ \begin{array}{lr} 0 & \textrm{ if } \textrm{pO}_{2,N} < \textrm{pO}_{2} \\ \\ d_{i,N}^* & \textrm{ if } \textrm{pO}_{2} \le \textrm{pO}_{2,N} \end{array}\right. \]
(Illustrative) parameter values
We use bi,P = 0.05 hour-1 (for a 20 hour cell cycle in physioxic conditions), di,A* = 0.01 bi,P, and di,N* = 0.04 hour-1 (so necrotic cells survive around 25 hours in low oxygen conditions).
We set α = 30 μM*hour (so that cells reach half max response after 6 hours’ exposure at a maximum concentration c = 5 μM), h = 2 (for a smooth effect), η = 0.25 (so that the drug is partly cytostatic), and di,Amax = 0.1 hour^-1 (so that cells survive about 10 hours after reaching maximum response).
Building the Cellular Automaton Model in BioFVM
BioFVM already includes Basic_Agents for cell-based substrate sources and sinks. We can extend these basic agents into full-fledged automata, and then arrange them in a lattice to create a full cellular automata model. Let’s sketch that out now.
Extending Basic_Agents to Automata
The main idea here is to define an Automaton class which extends (and therefore includes) the Basic_Agent class. This will give each Automaton full access to the microenvironment defined in BioFVM, including the ability to secrete and uptake substrates. We also make sure each Automaton “knows” which microenvironment it lives in (contains a pointer pMicroenvironment), and “knows” where it lives in the cellular automaton lattice. (More on that in the following paragraphs.)
So, as a schematic (just sketching out the most important members of the class):
class Standard_Data; // define per-cell biological data, such as phenotype,
// cell cycle status, etc..
class Custom_Data; // user-defined custom data, specific to a model.
class Automaton : public Basic_Agent
{
private:
Microenvironment* pMicroenvironment;
CA_Mesh* pCA_mesh;
int voxel_index;
protected:
public:
// neighbor connectivity information
std::vector<Automaton*> neighbors;
std::vector<double> neighbor_weights;
Standard_Data standard_data;
void (*current_state_rule)( Automaton& A , double );
Automaton();
void copy_parameters( Standard_Data& SD );
void overwrite_from_automaton( Automaton& A );
void set_cellular_automaton_mesh( CA_Mesh* pMesh );
CA_Mesh* get_cellular_automaton_mesh( void ) const;
void set_voxel_index( int );
int get_voxel_index( void ) const;
void set_microenvironment( Microenvironment* pME );
Microenvironment* get_microenvironment( void );
// standard state changes
bool attempt_division( void );
void become_apoptotic( void );
void become_necrotic( void );
void perform_lysis( void );
// things the user needs to define
Custom_Data custom_data;
// use this rule to add custom logic
void (*custom_rule)( Automaton& A , double);
};
So, the Automaton class includes everything in the Basic_Agent class, some Standard_Data (things like the cell state and phenotype, and per-cell settings), (user-defined) Custom_Data, basic cell behaviors like attempting division into an empty neighbor lattice site, and user-defined custom logic that can be applied to any automaton. To avoid lots of switch/case and if/then logic, each Automaton has a function pointer for its current activity (current_state_rule), which can be overwritten any time.
Each Automaton also has a list of neighbor Automata (their memory addresses), and weights for each of these neighbors. Thus, you can distance-weight the neighbors (so that corner elements are farther away), and very generalized neighbor models are possible (e.g., all lattice sites within a certain distance). When updating a cellular automaton model, such as to kill a cell, divide it, or move it, you leave the neighbor information alone, and copy/edit the information (standard_data, custom_data, current_state_rule, custom_rule). In many ways, an Automaton is just a bucket with a cell’s information in it.
Note that each Automaton also “knows” where it lives (pMicroenvironment and voxel_index), and knows what CA_Mesh it is attached to (more below).
Connecting Automata into a Lattice
An automaton by itself is lost in the world–it needs to link up into a lattice organization. Here’s where we define a CA_Mesh class, to hold the entire collection of Automata, setup functions (to match to the microenvironment), and two fundamental operations at the mesh level: copying automata (for cell division), and swapping them (for motility). We have provided two functions to accomplish these tasks, while automatically keeping the indexing and BioFVM functions correctly in sync. Here’s what it looks like:
class CA_Mesh{
private:
Microenvironment* pMicroenvironment;
Cartesian_Mesh* pMesh;
std::vector<Automaton> automata;
std::vector<int> iteration_order;
protected:
public:
CA_Mesh();
// setup to match a supplied microenvironment
void setup( Microenvironment& M );
// setup to match the default microenvironment
void setup( void );
int number_of_automata( void ) const;
void randomize_iteration_order( void );
void swap_automata( int i, int j );
void overwrite_automaton( int source_i, int destination_i );
// return the automaton sitting in the ith lattice site
Automaton& operator[]( int i );
// go through all nodes according to random shuffled order
void update_automata( double dt );
};
So, the CA_Mesh has a vector of Automata (which are never themselves moved), pointers to the microenvironment and its mesh, and a vector of automata indices that gives the iteration order (so that we can sample the automata in a random order). You can easily access an automaton with operator[], and copy the data from one Automaton to another with overwrite_automaton() (e.g, for cell division), and swap two Automata’s data (e.g., for cell migration) with swap_automata(). Finally, calling update_automata(dt) iterates through all the automata according to iteration_order, calls their current_state_rules and custom_rules, and advances the automata by dt.
Interfacing Automata with the BioFVM Microenvironment
The setup function ensures that the CA_Mesh is the same size as the Microenvironment.mesh, with same indexing, and that all automata have the correct volume, and dimension of uptake/secretion rates and parameters. If you declare and set up the Microenvironment first, all this is take care of just by declaring a CA_Mesh, as it seeks out the default microenvironment and sizes itself accordingly:
// declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // declare a Cellular_Automaton_Mesh CA_Mesh CA_model; // it's already good to go, initialized to empty automata: CA_model.display();
If you for some reason declare the CA_Mesh fist, you can set it up against the microenvironment:
// declare a CA_Mesh CA_Mesh CA_model; // declare a microenvironment Microenvironment M; // do things to set it up -- see prior tutorials // initialize the CA_Mesh to match the microenvironment CA_model.setup( M ); // it's already good to go, initialized to empty automata: CA_model.display();
Because each Automaton is in the microenvironment and inherits functions from Basic_Agent, it can secrete or uptake. For example, we can use functions like this one:
void set_uptake( Automaton& A, std::vector<double>& uptake_rates )
{
extern double BioFVM_CA_diffusion_dt;
// update the uptake_rates in the standard_data
A.standard_data.uptake_rates = uptake_rates;
// now, transfer them to the underlying Basic_Agent
*(A.uptake_rates) = A.standard_data.uptake_rates;
// and make sure the internal constants are self-consistent
A.set_internal_uptake_constants( BioFVM_CA_diffusion_dt );
}
A function acting on an automaton can sample the microenvironment to change parameters and state. For example:
void do_nothing( Automaton& A, double dt )
{ return; }
void microenvironment_based_rule( Automaton& A, double dt )
{
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// if pO2 < 5 mmHg, set the cell to a necrotic state
if( MS[0] < 5.0 ) { A.become_necrotic(); } // if drug > 5 uM, set the birth rate to zero
if( MS[1] > 5 )
{ A.standard_data.birth_rate = 0.0; }
// set the custom rule to something else
A.custom_rule = do_nothing;
return;
}
Implementing the mathematical model in this framework
We give each tumor cell a tumor_cell_rule (using this for custom_rule):
void viable_tumor_rule( Automaton& A, double dt )
{
// If there's no cell here, don't bother.
if( A.standard_data.state_code == BioFVM_CA_empty )
{ return; }
// sample the microenvironment
std::vector<double> MS = (*A.get_microenvironment())( A.get_voxel_index() );
// integrate drug exposure
A.standard_data.integrated_drug_exposure += ( MS[1]*dt );
A.standard_data.drug_response_function_value = pow( A.standard_data.integrated_drug_exposure,
A.standard_data.drug_hill_exponent );
double temp = pow( A.standard_data.drug_half_max_drug_exposure,
A.standard_data.drug_hill_exponent );
temp += A.standard_data.drug_response_function_value;
A.standard_data.drug_response_function_value /= temp;
// update birth rates (which themselves update probabilities)
update_birth_rate( A, MS, dt );
update_apoptotic_death_rate( A, MS, dt );
update_necrotic_death_rate( A, MS, dt );
return;
}
The functional tumor birth and death rates are implemented as:
void update_birth_rate( Automaton& A, std::vector<double>& MS, double dt )
{
static double O2_denominator = BioFVM_CA_physioxic_O2 - BioFVM_CA_necrotic_O2;
A.standard_data.birth_rate = A.standard_data.drug_response_function_value;
// response
A.standard_data.birth_rate *= A.standard_data.drug_max_birth_inhibition;
// inhibition*response;
A.standard_data.birth_rate *= -1.0;
// - inhibition*response
A.standard_data.birth_rate += 1.0;
// 1 - inhibition*response
A.standard_data.birth_rate *= viable_tumor_cell.birth_rate;
// birth_rate0*(1 - inhibition*response)
double temp1 = MS[0] ; // O2
temp1 -= BioFVM_CA_necrotic_O2;
temp1 /= O2_denominator;
A.standard_data.birth_rate *= temp1;
if( A.standard_data.birth_rate < 0 )
{ A.standard_data.birth_rate = 0.0; }
A.standard_data.probability_of_division = A.standard_data.birth_rate;
A.standard_data.probability_of_division *= dt;
// dt*birth_rate*(1 - inhibition*repsonse) // linearized probability
return;
}
void update_apoptotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.apoptotic_death_rate = A.standard_data.drug_max_death_rate;
// max_rate
A.standard_data.apoptotic_death_rate -= viable_tumor_cell.apoptotic_death_rate;
// max_rate - background_rate
A.standard_data.apoptotic_death_rate *= A.standard_data.drug_response_function_value;
// (max_rate-background_rate)*response
A.standard_data.apoptotic_death_rate += viable_tumor_cell.apoptotic_death_rate;
// background_rate + (max_rate-background_rate)*response
A.standard_data.probability_of_apoptotic_death = A.standard_data.apoptotic_death_rate;
A.standard_data.probability_of_apoptotic_death *= dt;
// dt*( background_rate + (max_rate-background_rate)*response ) // linearized probability
return;
}
void update_necrotic_death_rate( Automaton& A, std::vector<double>& MS, double dt )
{
A.standard_data.necrotic_death_rate = 0.0;
A.standard_data.probability_of_necrotic_death = 0.0;
if( MS[0] > BioFVM_CA_necrotic_O2 )
{ return; }
A.standard_data.necrotic_death_rate = perinecrotic_tumor_cell.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death = A.standard_data.necrotic_death_rate;
A.standard_data.probability_of_necrotic_death *= dt;
// dt*necrotic_death_rate
return;
}
And each fluid voxel (Dirichlet nodes) is implemented as the following (to turn on therapy at 21 days):
void fluid_rule( Automaton& A, double dt )
{
static double activation_time = 504;
static double activation_dose = 5.0;
static std::vector<double> activated_dirichlet( 2 , BioFVM_CA_physioxic_O2 );
static bool initialized = false;
if( !initialized )
{
activated_dirichlet[1] = activation_dose;
initialized = true;
}
if( fabs( BioFVM_CA_elapsed_time - activation_time ) < 0.01 ) { int ind = A.get_voxel_index(); if( A.get_microenvironment()->mesh.voxels[ind].is_Dirichlet )
{
A.get_microenvironment()->update_dirichlet_node( ind, activated_dirichlet );
}
}
}
At the start of the simulation, each non-cell automaton has its custom_rule set to fluid_rule, and each tumor cell Automaton has its custom_rule set to viable_tumor_rule. Here’s how:
void setup_cellular_automata_model( Microenvironment& M, CA_Mesh& CAM )
{
// Fill in this environment
double tumor_radius = 150;
double tumor_radius_squared = tumor_radius * tumor_radius;
std::vector<double> tumor_center( 3, 0.0 );
std::vector<double> dirichlet_value( 2 , 1.0 );
dirichlet_value[0] = 38; //physioxia
dirichlet_value[1] = 0; // drug
for( int i=0 ; i < M.number_of_voxels() ;i++ )
{
std::vector<double> displacement( 3, 0.0 );
displacement = M.mesh.voxels[i].center;
displacement -= tumor_center;
double r2 = norm_squared( displacement );
if( r2 > tumor_radius_squared ) // well_mixed_fluid
{
M.add_dirichlet_node( i, dirichlet_value );
CAM[i].copy_parameters( well_mixed_fluid );
CAM[i].custom_rule = fluid_rule;
CAM[i].current_state_rule = do_nothing;
}
else // tumor
{
CAM[i].copy_parameters( viable_tumor_cell );
CAM[i].custom_rule = viable_tumor_rule;
CAM[i].current_state_rule = advance_live_state;
}
}
}
Overall program loop
There are two inherent time scales in this problem: cell processes like division and death (happen on the scale of hours), and transport (happens on the order of minutes). We take advantage of this by defining two step sizes:
double BioFVM_CA_dt = 3; std::string BioFVM_CA_time_units = "hr"; double BioFVM_CA_save_interval = 12; double BioFVM_CA_max_time = 24*28; double BioFVM_CA_elapsed_time = 0.0; double BioFVM_CA_diffusion_dt = 0.05; std::string BioFVM_CA_transport_time_units = "min"; double BioFVM_CA_diffusion_max_time = 5.0;
Every time the simulation advances by BioFVM_CA_dt (on the order of hours), we run diffusion to quasi-steady state (for BioFVM_CA_diffusion_max_time, on the order of minutes), using time steps of size BioFVM_CA_diffusion time. We performed numerical stability and convergence analyses to determine 0.05 min works pretty well for regular lattice arrangements of cells, but you should always perform your own testing!
Here’s how it all looks, in a main program loop:
BioFVM_CA_elapsed_time = 0.0;
double next_output_time = BioFVM_CA_elapsed_time; // next time you save data
while( BioFVM_CA_elapsed_time < BioFVM_CA_max_time + 1e-10 )
{
// if it's time, save the simulation
if( fabs( BioFVM_CA_elapsed_time - next_output_time ) < BioFVM_CA_dt/2.0 )
{
std::cout << "simulation time: " << BioFVM_CA_elapsed_time << " " << BioFVM_CA_time_units
<< " (" << BioFVM_CA_max_time << " " << BioFVM_CA_time_units << " max)" << std::endl;
char* filename;
filename = new char [1024];
sprintf( filename, "output_%6f" , next_output_time );
save_BioFVM_cellular_automata_to_MultiCellDS_xml_pugi( filename , M , CA_model ,
BioFVM_CA_elapsed_time );
cell_counts( CA_model );
delete [] filename;
next_output_time += BioFVM_CA_save_interval;
}
// do the cellular automaton step
CA_model.update_automata( BioFVM_CA_dt );
BioFVM_CA_elapsed_time += BioFVM_CA_dt;
// simulate biotransport to quasi-steady state
double t_diffusion = 0.0;
while( t_diffusion < BioFVM_CA_diffusion_max_time + 1e-10 )
{
M.simulate_diffusion_decay( BioFVM_CA_diffusion_dt );
M.simulate_cell_sources_and_sinks( BioFVM_CA_diffusion_dt );
t_diffusion += BioFVM_CA_diffusion_dt;
}
}
Getting and Running the Code
- Start a project: Create a new directory for your project (I’d recommend “BioFVM_CA_tumor”), and enter the directory. Place a copy of BioFVM (the zip file) into your directory. Unzip BioFVM, and copy BioFVM*.h, BioFVM*.cpp, and pugixml* files into that directory.
- Download the demo source code: Download the source code for this tutorial: BioFVM_CA_Example_1, version 1.0.0 or later. Unzip its contents into your project directory. Go ahead and overwrite the Makefile.
- Edit the makefile (if needed): Note that if you are using OSX, you’ll probably need to change from “g++” to your installed compiler. See these tutorials.
- Test the code: Go to a command line (see previous tutorials), and test:
make ./BioFVM_CA_Example_1
(If you’re on windows, run BioFVM_CA_Example_1.exe.)
Simulation Result
If you run the code to completion, you will simulate 3 weeks of in vitro growth, followed by a bolus “injection” of drug. The code will simulate one one additional week under the drug. (This should take 5-10 minutes, including full simulation saves every 12 hours.)
In matlab, you can load a saved dataset and check the minimum oxygenation value like this:
MCDS = read_MultiCellDS_xml( 'output_504.000000.xml' ); min(min(min( MCDS.continuum_variables(1).data )))
And then you can start visualizing like this:
contourf( MCDS.mesh.X_coordinates , MCDS.mesh.Y_coordinates , ...
MCDS.continuum_variables(1).data(:,:,33)' ) ;
axis image;
colorbar
xlabel('x (\mum)' , 'fontsize' , 12 );
ylabel( 'y (\mum)' , 'fontsize', 12 );
set(gca, 'fontsize', 12 );
title('Oxygenation (mmHg) at z = 0 \mum', 'fontsize', 14 );
print('-dpng', 'Tumor_o2_3_weeks.png' );
plot_cellular_automata( MCDS , 'Tumor spheroid at 3 weeks');
Simulation plots
Here are some plots, showing (left from right) pO2 concentration, a cross-section of the tumor (red = live cells, green = apoptotic, and blue = necrotic), and the drug concentration (after start of therapy):
1 week:
Oxygen- and space-limited growth are restricted to the outer boundary of the tumor spheroid.
2 weeks:
Oxygenation is dipped below 5 mmHg in the center, leading to necrosis.
3 weeks:
As the tumor grows, the hypoxic gradient increases, and the necrotic core grows. The code turns on a constant 5 micromolar dose of doxorubicin at this point
Treatment + 12 hours:
The drug has started to penetrate the tumor, triggering apoptotic death towards the outer periphery where exposure has been greatest.
Treatment + 24 hours:
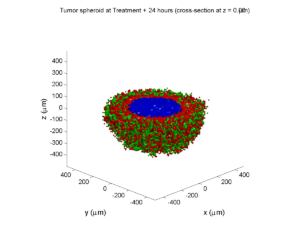
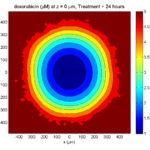
The drug profile hasn’t changed much, but the interior cells have now had greater exposure to drug, and hence greater response. Now apoptosis is observed throughout the non-necrotic tumor. The tumor has decreased in volume somewhat.
Treatment + 36 hours:
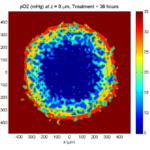
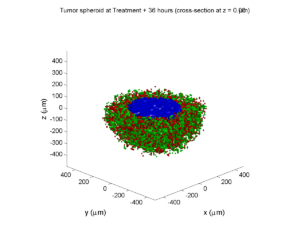
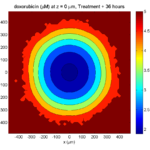
The non-necrotic tumor is now substantially apoptotic. We would require some pharamcokinetic effects (e.g., drug clearance, inactivation, or removal) to avoid the inevitable, presences of a pre-existing resistant strain, or emergence of resistance.
Treatment + 48 hours:
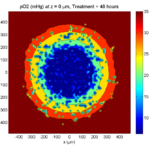
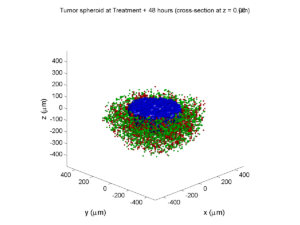
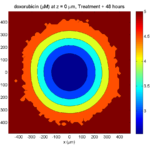
By now, almost all cells are apoptotic.
Treatment + 60 hours:

The non-necrotic tumor is nearly completed eliminated, leaving a leftover core of previously-necrotic cells (which did not change state in response to the drug–they were already dead!)
Source files
You can download completed source for this example here: https://sourceforge.net/projects/biofvm/files/Tutorials/Cellular_Automaton_1/
This file will include the following:
- BioFVM_cellular_automata.h
- BioFVM_cellular_automata.cpp
- BioFVM_CA_example_1.cpp
- read_MultiCellDS_xml.m (updated)
- plot_cellular_automata.m
- Makefile
What’s next
I plan to update this source code with extra cell motility, and potentially more realistic parameter values. Also, I plan to more formally separate out the example from the generic cell capabilities, so that this source code can work as a bona fide cellular automaton framework.
More immediately, my next tutorial will use the reverse strategy: start with an existing cellular automaton model, and integrate BioFVM capabilities.
Return to News • Return to MathCancer • Follow @MathCancer
BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations
I’m very excited to announce that our 3-D diffusion solver has been accepted for publication and is now online at Bioinformatics. Click here to check out the open access preprint!
A. Ghaffarizadeh, S.H. Friedman, and P. Macklin. BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations. Bioinformatics, 2015.
DOI: 10.1093/bioinformatics/btv730 (free; open access)
BioFVM (stands for “Finite Volume Method for biological problems) is an open source package to solve for 3-D diffusion of several substrates with desktop workstations, single supercomputer nodes, or even laptops (for smaller problems). We built it from the ground up for biological problems, with optimizations in C++ and OpenMP to take advantage of all those cores on your CPU. The code is available at SourceForge and BioFVM.MathCancer.org.
The main idea here is to make it easier to simulate big, cool problems in 3-D multicellular biology. We’ll take care of secretion, diffusion, and uptake of things like oxygen, glucose, metabolic waste products, signaling factors, and drugs, so you can focus on the rest of your model.
Design philosophy and main capabilities
Solving diffusion equations efficiently and accurately is hard, especially in 3D. Almost all biological simulations deal with this, many by using explicit finite differences (easy to code and accurate, but very slow!) or implicit methods like ADI (accurate and relatively fast, but difficult to code with complex linking to libraries). While real biological systems often depend upon many diffusing things (lots of signaling factors for cell-cell communication, growth substrates, drugs, etc.), most solvers only scale well to simulating two or three. We solve a system of PDEs of the following form:
\[ \frac{\partial \vec{\rho}}{\partial t} = \overbrace{ \vec{D} \nabla^2 \vec{\rho} }^\textrm{diffusion}
– \overbrace{ \vec{\lambda} \vec{\rho} }^\textrm{decay} + \overbrace{ \vec{S} \left( \vec{\rho}^* – \vec{\rho} \right) }^{\textrm{bulk source}} – \overbrace{ \vec{U} \vec{\rho} }^{\textrm{bulk uptake}} + \overbrace{\sum_{\textrm{cells } k} 1_k(\vec{x}) \left[ \vec{S}_k \left( \vec{\rho}^*_k – \vec{\rho} \right) – \vec{U}_k \vec{\rho} \right] }^\textrm{sources and sinks by cells} \]
Above, all vector-vector products are term-by-term.
Solving for many diffusing substrates
We set out to write a package that could simulate many diffusing substrates using algorithms that were fast but simple enough to optimize. To do this, we wrote the entire solver to work on vectors of substrates, rather than on individual PDEs. In performance testing, we found that simulating 10 diffusing things only takes about 2.6 times longer than simulating one. (In traditional codes, simulating ten things takes ten times as long as simulating one.) We tried our hardest to break the code in our testing, but we failed. We simulated all the way from 1 diffusing substrate up to 128 without any problems. Adding new substrates increases the computational cost linearly.
Combining simple but tailored solvers
We used an approach called operator splitting: breaking a complicated PDE into a series of simpler PDEs and ODEs, which can be solved one at a time with implicit methods. This allowed us to write a very fast diffusion/decay solver, a bulk supply/uptake solver, and a cell-based secretion/uptake solver. Each of these individual solvers was individually optimized. Theory tells us that if each individual solver is first-order accurate in time and stable, then the overall approach is first-order accurate in time and stable.
The beauty of the approach is that each solver can individually be improved over time. For example, in BioFVM 1.0.2, we doubled the performance of the cell-based secretion/uptake solver. The operator splitting approach also lets us add new terms to the “main” PDE by writing new solvers, rather than rewriting a large, monolithic solver. We will take advantage of this to add advective terms (critical for interstitial flow) in future releases.
Optimizing the diffusion solver for large 3-D domains
For the first main release of BioFVM, we restricted ourselves to Cartesian meshes, which allowed us to write very tailored mesh data structures and diffusion solvers. (Note: the finite volume method reduces to finite differences on Cartesian meshes with trivial Neumann boundary conditions.) We intend to work on more general Voronoi meshes in a future release. (This will be particularly helpful for sources/sinks along blood vessels.)
By using constant diffusion and decay coefficients, we were able to write very fast solvers for Cartesian meshes. We use the locally one-dimensional (LOD) method–a specialized form of operator splitting–to break the 3-D diffusion problem into a series of 1-D diffusion problems. For each (y,z) in our mesh, we have a 1-D diffusion problem along x. This yields a tridiagonal linear system which we can solve efficiently with the Thomas algorithm. Moreover, because the forward-sweep steps only depend upon the coefficient matrix (which is unchanging over time), we can pre-compute and store the results in memory for all the x-diffusion problems. In fact, the structure of the matrix allows us to pre-compute part of the back-substitution steps as well. Same for y- and z-diffusion. This gives a big speedup.
Next, we can use all those CPU cores to speed up our work. While the back-substitution steps of the Thomas algorithm can’t be easily parallelized (it’s a serial operation), we can solve many x-diffusion problems at the same time, using independent copies (instances) of the Thomas solver. So, we break up all the x-diffusion problems up across a big OpenMP loop, and repeat for y– and z-diffusion.
Lastly, we used overloaded +=, axpy and similar operations on the vector of substrates, to avoid unnecessary (and very expensive) memory allocation and copy operations wherever we could. This was a really fun code to write!
The work seems to have payed off: we have found that solving on 1 million voxel meshes (about 8 mm3 at 20 μm resolution) is easy even for laptops.
Simulating many cells
We tailored the solver to allow both lattice- and off-lattice cell sources and sinks. Desktop workstations should have no trouble with 1,000,000 cells secreting and uptaking a few substrates.
Simplifying the non-science
We worked to minimize external dependencies, because few things are more frustrating than tracking down a bunch of libraries that may not work together on your platform. The first release BioFVM only has one external dependency: pugixml (an XML parser). We didn’t link an entire linear algebra library just to get axpy and a Thomas solver–it wouldn’t have been optimized for our system anyway. We implemented what we needed of the freely available .mat file specification, rather than requiring a separate library for that. (We have used these matlab read/write routines in house for several years.)
Similarly, we stuck to a very simple mesh data structure so we wouldn’t have to maintain compatibility with general mesh libraries (which can tend to favor feature sets and generality over performance and simplicity). Rather than use general-purpose ODE solvers (with yet more library dependencies, and more work for maintaining compatibility), we wrote simple solvers tailored specifically to our equations.
The upshot of this is that you don’t have to do anything fancy to replicate results with BioFVM. Just grab a copy of the source, drop it into your project directory, include it in your project (e.g., your makefile), and you’re good to go.
All the juicy details
The Bioinformatics paper is just 2 pages long, using the standard “Applications Note” format. It’s a fantastic format for announcing and disseminating a piece of code, and we’re grateful to be published there. But you should pop open the supplementary materials, because all the fun mathematics are there:
- The full details of the numerical algorithm, including information on our optimizations.
- Convergence tests: For several examples, we showed:
- First-order convergence in time (with respect to Δt), and stability
- Second-order convergence in space (with respect to Δx)
- Accuracy tests: For each convergence test, we looked at how small Δt has to be to ensure 5% relative accuracy at Δx = 20 μm resolution. For oxygen-like problems with cell-based sources and sinks, Δt = 0.01 min will do the trick. This is about 15 times larger than the stability-restricted time step for explicit methods.
- Performance tests:
- Computational cost (wall time to simulate a fixed problem on a fixed domain size with fixed time/spatial resolution) increases linearly with the number of substrates. 5-10 substrates are very feasible on desktop workstations.
- Computational cost increases linearly with the number of voxels
- Computational cost increases linearly in the number of cell-based source/sinks
And of course because this code is open sourced, you can dig through the implementation details all you like! (And improvements are welcome!)
What’s next?
- As MultiCellDS (multicellular data standard) matures, we will implement read/write support for <microenvironment> data in digital snapshots.
- We have a few ideas to improve the speed of the cell-based sources and sinks. In particular, switching to a higher-order accurate solver may allow larger time step sizes, so long as the method is still stable. For the specific form of the sources/sinks, the trapezoid rule could work well here.
- I’d like to allow a spatially-varying diffusion coefficient. We could probably do this (at very great memory cost) by writing separate Thomas solvers for each strip in x, y, and z, or by giving up the pre-computation part of the optimization. I’m still mulling this one over.
- I’d also like to implement non-Cartesian meshes. The data structure isn’t a big deal, but we lose the LOD optimization and Thomas solvers. In this case, we’d either use explicit methods (very slow!), use an iterative matrix solver (trickier to parallelize nicely, except in matrix-vector multiplication operations), or start with quasi-steady problems that let us use Gauss-Seidel iterative type methods, like this old paper.
- Since advective flow (particularly interstitial flow) is so important for many problems, I’d like to add an advective solver. This will require some sort of upwinding to maintain stability.
- At some point, we’d like to port this to GPUs. However, I don’t currently have time / resources to maintain a separate CUDA or OpenCL branch. (Perhaps this will be an excuse to learn Julia on GPUs.)
Well, we hope you find BioFVM useful. If you give it a shot, I’d love to hear back from you!
Very best — Paul
Paul Macklin calls for common standards in cancer modeling
At a recent NCI-organized mini-symposium on big data in cancer, Paul Macklin called for new data standards in Multicellular data in simulations, experiments, and clinical science. USC featured the talk (abstract here) and the work at news.usc.edu.
Read the article: http://news.usc.edu/59091/usc-researcher-calls-for-common-standards-in-cancer-modeling/ (Feb. 21, 2014)